This set of Manufacturing Engineering Multiple Choice Questions & Answers (MCQs) focuses on “Miller Indices”.
1. Stacking sequence in hexagonal close packed (HCP) structure is?
a) AAAAA
b) ABABAB
c) ABCABC
d) AABBAA
View Answer
Explanation: The geometry of close packed hexagonal unit cell can be understood from the below figure, which indicates a plane view of atoms.
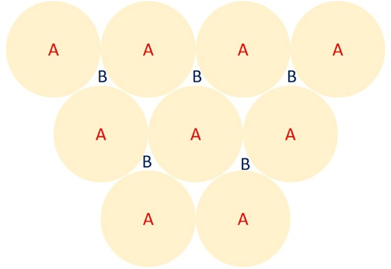
Figure: Stacking sequences of close packed layers of atoms. A-first layer (with outlines of atoms shown in gold colour); B-second layer.
A is the first layer (with the circular outlines of the atoms drawn in gold colour) and B is the second layer (outlines of the atoms not shown for clarity). In hexagonal close packed unit cell, the third layer of atoms go directly above the A layer, the fourth layer over the B layer, and so on; the sequence becomes ABABAB.
2. Stacking sequence in face centered cubic (FCC) close packed structure is?
a) AAAAA
b) ABABAB
c) ABCABC
d) AABBAA
View Answer
Explanation: The stacking sequence in FCC can be best understood from the below figure.
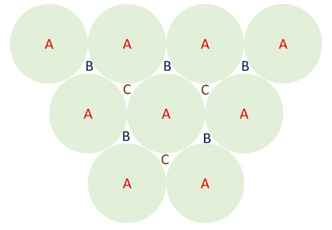
Figure: Stacking sequences of close packed layers of atoms. A-first layer (with outlines of atoms shown in green colour); B-second layer; C-third layer.
A is the first layer (with the circular outlines of the atoms drawn in green colour) and B is the second layer (outlines of the atoms not shown for clarity). The third layer of atoms goes above the interstices marked C and the sequence only repeats at the fourth layer, which goes directly above the first layer. Thus, the stacking sequence is now ABCABC.
3. For pane (1 1 1) of FCC having a lattice parameter ‘a’, planar atomic density is given by?
a) 2.31/a2
b) 2.31/a3
c) 1.31/a2
d) 1.31/a3
View Answer
Explanation: Upon visualizing (1 1 1) plane of FCC, one can identify that there the equilibrium triangle (1 1 1) of FCC consists 2 atoms (1⁄6×3 + 1⁄2×3=2). Also, the area of the equilibrium triangle (1 1 1) is 0.886 a2.
Therefore, the number of atoms per square inch which is nothing but its planar density = \(\frac{2}{0.866 a^2} = \frac{2.31}{a^2}\).
4. For pane (1 1 1) of BCC having a lattice parameter ‘a’, planar atomic density is given by?
a) 1.07/a2
b) 0.58/a2
c) 2.07/a2
d) 0.78/a2
View Answer
Explanation: From the geometry of the triangle (1 1 1), it is clear that it has 0.5 atoms in it (1/6×3 = 0.5) and the area of the triangle (1 1 1) is 0.866 a2.
Therefore, the number of atoms per square inch which is nothing but its planar density = \(\frac{0.5}{0.866 a^2} = \frac{0.58}{a^2}\).
5. For pane (1 0 0) of BCC having a lattice parameter ‘a’, planar atomic density is given by?
a) 1/a3
b) 2/a2
c) 3/a4
d) 1/a2
View Answer
Explanation: The atomic arrangement on square (1 0 0) of BCC indicates that it has 1 atom and area of this square (1 0 0) is a2. Thus, its planar density = 1/a2.
6. For pane (1 1 0) of BCC having a lattice parameter ‘a’, planar atomic density is given by?
a) 3.690/a2
b) 2.312/a2
c) 1.414/a2
d) 0.580/a2
View Answer
Explanation: From the geometry of the rectangle (1 1 0), it is clear that it has 2 atoms in it (1⁄4×4+1=2) and the area of the rectangle (1 1 0) is 0.866 a2.
Therefore, the number of atoms per square inch which is nothing but its planar density = \(\frac{2}{1.414 a^2} = \frac{1.414}{a^2}\).
7. For pane (1 1 0) of SC having a lattice parameter ‘a’, planar atomic density is given by?
a) 0.508/a2
b) 0.707/a2
c) 0.707/a3
d) 0.508/a3
View Answer
Explanation: The atomic arrangement on (1 1 0) plane in simple cubic (SC) unit cell indicates that it has 1 atom (1⁄4×4=1) in this plane having an area = \(\sqrt{2} a^2\).
Therefore, the number of atoms per square inch which is nothing but its planar density = \(\frac{1}{1.414 a^2} = \frac{0.707}{a^2}\).
8. For pane (1 1 1) of SC having a lattice parameter ‘a’, planar atomic density is given by?
a) 0.58/a2
b) 0.78/a3
c) 0.68/a2
d) 0.88/a2
View Answer
Explanation: The atomic arrangement on triangle (1 1 1) in simple cubic (SC) unit cell indicates that it has 0.5 atoms (1⁄6×3=0.5) in this plane having an area = 0.866 a2.
Therefore, the number of atoms per square inch which is nothing but its planar density = \(\frac{0.5}{0.866 a^2} = \frac{0.577}{a^2}\).
9. Which of the following equation describes Bragg’s law of diffraction? (Assume that all symbols have their usual meaning.)
a) 2d sinθ = λ
b) 2d = nλ
c) 2d = nλ sinθ
d) 2d sinθ = nλ
View Answer
Explanation: Bragg’s law, which describes the constructive interference conditions for θ to be at its strongest: nλ = 2d sinθ, where λ is the wavelength of the incident wave and and n is the order of diffraction which is always a positive integer and d is the interplanar spacing and θ = angle of diffraction. This equation can be easily derived upon constructing a basic wave reflection diagram taking incident angle as θ.
10. Powder X-ray technique can be used to determine crystal structures.
a) True
b) False
View Answer
Explanation: The powder method is used to determine the values of lattice parameters accurately. As we know, lattice parameters defines the axis system, which in turns can predict the crystal structure of the powder sampled.
Sanfoundry Global Education & Learning Series – Manufacturing Engineering.
To practice all areas of Manufacturing Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Manufacturing Processes I Books
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
- Practice Mechanical Engineering MCQs
- Check Metallurgical Engineering Books
