This set of Manufacturing Engineering Multiple Choice Questions & Answers (MCQs) focuses on “Introduction To Composites”.
1. Composites can be classified based on ___________
a) matrix type
b) reinforcement constituent
c) matrix type & Reinforcement constituent
d) neither on matrix type nor on reinforcement constituent type
View Answer
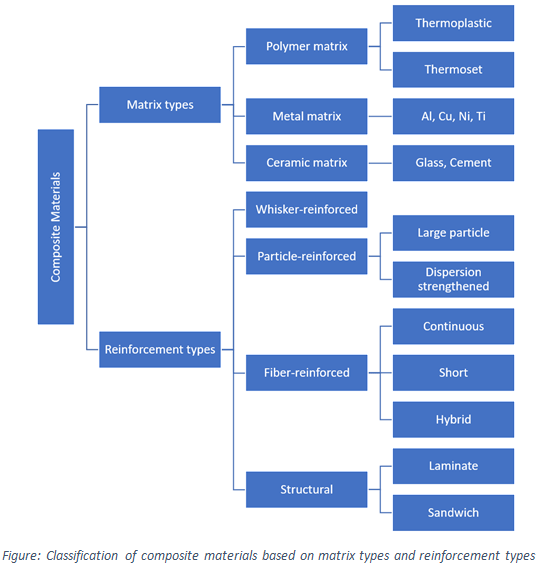
Explanation: Composites cans be classified based on matrix types and reinforcement constituent types as shown below:
2. Which of the following is not a laminar composite?
a) Bimetallic
b) Cladding
c) Paints
d) Wood
View Answer
Explanation: Wood is not a laminar composite. Bimetallic, cladding and paints are considered as laminar composites.
3. The composite constituents of both matrix and reinforcements are softer.
a) True
b) False
View Answer
Explanation: Matrix constituents are generally softer whereas reinforced constituents provide hardness to the composites.
4. In sandwich composites, which of the following material can be used for filling purpose?
a) Wood
b) Cement
c) Polymer
d) All of the mentioned
View Answer
Explanation: Wood, cement, and polymer can be used to fill the gap in sandwich composites.
5. Which of the following have a greater impact on longitudinal strength of reinforced composites?
a) Fiber orientation
b) Fiber strength
c) Fiber length
d) Fiber diameter
View Answer
Explanation: Longitudinal strength of reinforced composites is directly proportional to its fiber strength.
6. Which of the following may alter the mechanical properties of reinforced composites?
a) Constituent properties
b) Fiber length
c) Fiber orientation
d) All of the mentioned
View Answer
Explanation: Constituent properties, fiber length etc affect the overall property of reinforced composites.
7. Which of the following property can be enhanced by reinforcing an aluminum alloy?
a) Density
b) Torsion resistance
c) Wear resistance
d) Strength
View Answer
Explanation: It is observed that for an aluminium alloy matrix composites when reinforced with ceramic particles, there is an increase in the wear resistance.
8. Which of the following is the correct size range of dispersoids (in micrometres) in dispersion strengthened composites?
a) 0.0001-0.0009
b) 0.01-0.1
c) 0.1-1.0
d) 2.0-2.7
View Answer
Explanation: Dispersoids size varies from 0.01 micrometre to 0.1 micrometre. They are very small.
9. Which of the following is correct dimensional of flake composites?
a) 1-Dimensional
b) 2-Dimensional
c) 3-Dimensional
d) 4-Dimensional
View Answer
Explanation: Flake composites are two dimensional in nature and can be easily represented on a plane of the paper.
10. Fire point of composite is high.
a) True
b) False
View Answer
Explanation: Composites have low fire and flash point, and this is one of the main drawbacks.
Sanfoundry Global Education & Learning Series – Manufacturing Engineering.
To practice all areas of Manufacturing Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Check Mechanical Engineering Books
- Apply for Metallurgical Engineering Internship
- Practice Metallurgical Engineering MCQs
- Check Metallurgical Engineering Books
- Check Manufacturing Processes I Books
