This set of Engineering Drawing Multiple Choice Questions & Answers (MCQs) focuses on “Drawing Tangents and Normals for Different Conditions of Circle – 1”.
1. Given are the steps to draw a tangent to any given circle at any point P on it. Arrange the steps.
i. Draw the given circle with center O and mark the point P anywhere on the circle.
ii. With centers O and Q draw arcs with equal radius to cut each other at R.
iii. Join R and P which is the required tangent.
iv. Draw a line joining O and P. Extend the line to Q such that OP = PQ.
a) i, iv, ii, iii
b) iv, i, iii, ii
c) iii, i, iv, ii
d) ii, iv, i, iii
View Answer
Explanation: Tangent is a line which touches a curve at only one point. Every tangent is perpendicular to its normal. Here we first found the normal which passes through center and point. Then drawing a perpendicular to it gives the tangent.
2. Given are the steps to draw a tangent to given circle from any point outside the circle. Arrange the steps.
i. With OP as diameter, draw arcs on circle at R and R1.
ii. Draw the given circle with center O.
iii. Join P and R which is one tangent and PR1 is another tangent.
iv. Mark the point P outside the circle.
a) ii, iv, iii, i
b) iv, i, iii, ii
c) iii, i, iv, ii
d) ii, iv, i, iii
View Answer
Explanation: Usually when a point is outside the circle there exists two tangents. For which we first join the center with point P and then taking distance from center to P as diameter circle is drawn from the midpoint of center and P to cut circle at two points where tangents touch the circle.
3. Given are the steps to draw a tangent to given arc even if center is unknown and the point P lies on it. Arrange the steps. Let AB be the arc.
i. Draw EF, the bisector of the arc CD. It will pass through P.
ii. RS is the required tangent.
iii. With P as center and any radius draw arcs cutting arc AB at C and D.
iv. Draw a perpendicular RS to EF through P.
a) ii, iv, iii, i
b) iv, i, iii, ii
c) iii, i, iv, ii
d) ii, iv, i, iii
View Answer
Explanation: Even if the center of the arc is unknown, just by taking any some part of arc and bisecting that with a line at required point p gives us normal to tangent at P. So then from normal drawing perpendicular gives our required tangent.
4. Given are the steps to draw a tangent to given circle and parallel to given line. Arrange the steps.
i. Draw a perpendicular to given line and extend to cut the circle at two points P and Q.
ii. At P or Q draw perpendicular to normal then we get the tangents.
iii. PQ is the normal for required tangent.
iv. Draw a circle with center O and line AB as required.
a) ii, iv, iii, i
b) iv, i, iii, ii
c) iii, i, iv, ii
d) ii, iv, i, iii
View Answer
Explanation: Normal of curve will be perpendicular to every parallel tangent at that point. We just drawn the longest chord (diameter) and then perpendicular it gives the required tangents. Since circle is closed figure there exist two tangents parallel to each other.
5. How many external tangents are there for two circles?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: External tangents are those which touch both the circles but they will not intersect in between the circles. The tangents touch at outmost points of circles that are ends of diameter if the circles have the same diameter.
6. How many internal tangents are there for two circles?
a) 4
b) 3
c) 2
d) 1
View Answer
Explanation: Internal tangents are those which touch both the circle and also intersect each other on the line joining the centers of circles. And the internal tangents intersect each other at midpoint of line joining the center of circles only if circles have the same diameter.
7. For any point on any curve there exist two normals.
a) True
b) False
View Answer
Explanation: Here we take point on the curve. There exist multiple tangents for some curve which are continuous, trigonometric curves, hyperbola etc. But for curves like circles, parabola, ellipse, cycloid etc. have only one tangent and normal.
8. Arrange the steps. These give procedure to draw internal tangent to two given circles of equal radii.
i. Draw a line AB which is the required tangent.
ii. Draw the given circles with centers O and P.
iii. With center R and radius RA, draw an arc to intersect the other circle on the other circle on the other side of OP at B.
iv. Bisect OP in R. Draw a semi circle with OR as diameter to cut the circle at A.
a) ii, iv, iii, i
b) iv, i, iii, ii
c) iii, i, iv, ii
d) ii, iv, i, iii
View Answer
Explanation: Since the circles have same radius. The only two internal tangents will intersect at midpoint of line joining the centers. So we first found the center and then point of intersection of tangent and circle then from that point to next point it is drawn a arc midpoint as center and join the points gave us tangent.
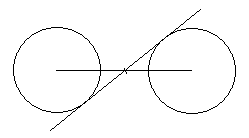
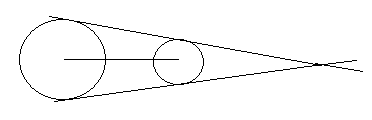
9. There are 2 circles say A, B. A has 20 units radius and B has 10 units radius and distance from centers of A and B is 40 units. Where will be the intersection point of external tangents?
a) to the left of two circles
b) to the right of the two circles
c) middle of the two circles
d) they intersect at midpoint of line joining the centers
View Answer
Explanation: A has 20 units radius and B has 10 units radius. So, the tangents go along the circles and meet at after the second circle that is B that is the right side of both circles. And we asked for external tangents so they meet away from the circles but not in between them.
10. There are 2 circles say A, B. A is smaller than B and they are not intersecting at any point. Where will be the intersection point of internal tangents for these circles?
a) to the left of two circles
b) to the right of the two circles
c) middle of the two circles
d) they intersect at midpoint of line joining the centers
View Answer
Explanation: A is smaller than B so the intersection point of internal tangents will not be on the midpoint of the line joining the centers. And we asked for internal tangents so they will not meet away from the circles. They meet in between them.
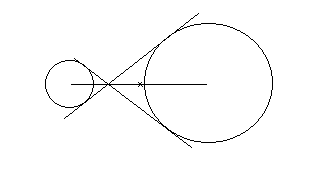
Sanfoundry Global Education & Learning Series – Engineering Drawing.
To practice all areas of Engineering Drawing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
