This set of Engineering Drawing Questions and Answers for Freshers focuses on “Drawing Tangents and Normals for Different Conditions of Circle – 2”.
1. A tangent to a circle is a line which touches the circle at one and only one point.
a) True
b) False
View Answer
Explanation: A tangent to a circle is a line which touches the circle at one and only one point. The line joining the centre of the circle and that one point whose length is equal to the radius is perpendicular to the tangent.
2. The line perpendicular to a tangent and is passing through the point of contact is called as _____
a) Perpendicular bisector
b) Angle bisector
c) Normal
d) Tangent
View Answer
Explanation: The line perpendicular to a tangent and is passing through the point of contact is called as the normal. The line joining the centre and the point of contact is perpendicular to the tangent and hence can be called as normal to the tangent.
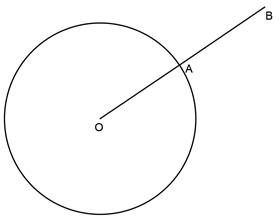
3. In the following figure, the tangent at point A can be drawn by _______
a) Angle bisector
b) Perpendicular bisector
c) Rectangle
d) Arc
View Answer
Explanation: In the given figure, the tangent to the circle with centre O at point A can be drawn by using the property of perpendicular bisector. Since from the figure it is clear that the length of OA is equal to the length of AB and the perpendicular bisector of OB is the tangent at A.
4. How many tangents can be drawn from a point outside a given circle?
a) 4
b) 3
c) 2
d) 1
View Answer
Explanation: Two tangents can be drawn from a point outside a given circle. The method to draw tangent to the circle first involves joining the point and the centre and then drawing a semicircle with that length as diameter. Then join the intersection points on the circle and the point outside you get the tangent.
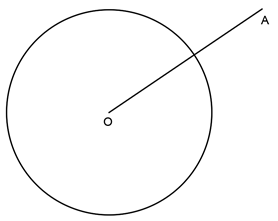
5. In the following figure, how will make a tangent from the point outside the circle?
a) By drawing a semicircle with diameter as OA
b) By drawing a perpendicular bisector
c) By drawing an angle bisector
d) By drawing circle with the same radius from A
View Answer
Explanation: In the given figure, we can draw a tangent from the point outside i.e. point A to the circle by drawing a semicircle with a diameter as OA. The intersection point of this semicircle with the circle is joined with the point A to form the tangent.
6. How many tangents to a given circle, can we draw parallel to a given line?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: We can draw two tangents to a given circle which will be parallel to a given line. The given line can be outside or inside the circle but we can draw two parallel lines tangent to the circle. Both the lines will touch the circle at one and only one point respectively.
7. In how many ways can there be a common tangent between two circles?
a) 3
b) 4
c) 1
d) 2
View Answer
Explanation: There are two ways in which the circles can have a common tangent. One is internal tangents in which the common tangent is touching the internal part of the circle with respect to the other circle and the other way is external tangent.
8. How many internally common tangents can two circles have?
a) 3
b) 1
c) 2
d) 4
View Answer
Explanation: Two circles can have two internally touching common tangents. Both the tangents intersect at a point which is equidistant from the centers of both the circles. In other words, they intersect at a point which bisects the line joining the centers of the circles.
9. To draw a tangent to an arc of unknown radius and centre through any point on the arc we use ________
a) Angle bisectors
b) Semicircles
c) Arc
d) Perpendicular bisector
View Answer
Explanation: To draw a tangent to an arc of an unknown radius and a centre through any point on the arc we the principle of perpendicular bisectors. First, we cut the arc at two sides of the point by an arc of any radius and we use perpendicular bisector to draw the normal and from there we draw the tangent.
10. How is a normal to a tangent drawn?
a) Angle bisector
b) Perpendicular bisector
c) Rectangle
d) Semicircle
View Answer
Explanation: We draw a normal to a tangent by using perpendicular bisector. Cut the tangent at two points on both sides of the point of contact and then keeping center at the new intersection points cut another arc on the up and down of the point of contact. Join these points and you get normal.
Sanfoundry Global Education & Learning Series – Engineering Drawing.
To practice all areas of Engineering Drawing for Freshers, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
