This set of Engineering Drawing Multiple Choice Questions & Answers (MCQs) focuses on “Basic Geometrical Construction & Involute Section”.
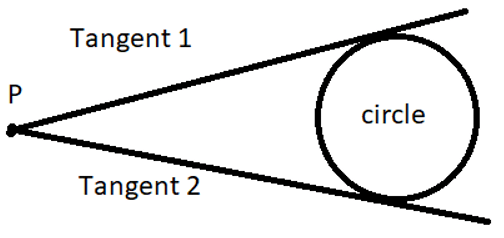
1. The number of tangents that can be drawn to a circle from a point outside is___
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Here P is a point where 2 tangents are drawn for a circle.
Tangent – A straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point.
2. The number of common tangents that can be drawn to two circles which touch each other externally?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Tangent – A straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point.
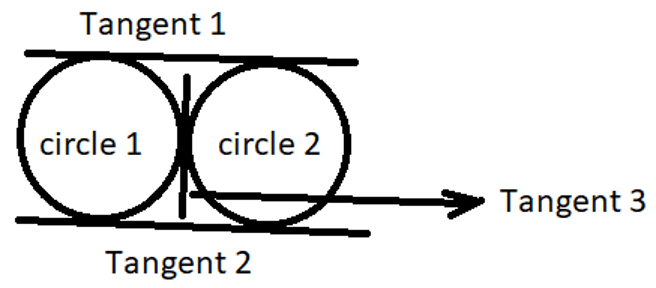
An external tangent connecting two circles of equal radii is parallel to the line joining centers.
3. Number of diagonal that a hexagon can have?
a) 3
b) 6
c) 9
d) 12
View Answer
Explanation: A hexagon is a 6-sided polygon, so to determine the number of diagonals a hexagon has, we plug n = 6 into the formula n.(n-3)/2, where n is number of sides. We see that a hexagon has 9 diagonals.
4. A polygon having the sum of the measures of the interior angles equal the sum of the measures of the exterior angles is?
a) Triangle
b) Quadrilateral
c) Hexagon
d) Octagon
View Answer
Explanation: A quadrilateral is a polygon with 4 edges and 4 vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon, hexagon and so on.
5. The included angle of a pentagon is_____
a) 68°
b) 72°
c) 108°
d) 112°
View Answer
Explanation: A regular polygon is a flat shape whose sides are all equal and whose angles are all equal. The formula for finding the sum of the measures of the interior angles is (n-2)*180.To find the measure of one interior angle, we take that formula and divide by the number of sides (n) : (n-2)*180/n.
6. Divide the given straight line of 80cm into 7 equal parts and what will be the length of each part?
a) 11.32
b) 11.42
c) 11.52
d) 11.35
View Answer
Explanation: Draw the line segment AB of the given length and draw an acute angle to AB. In that line use circle arcs of the same radius to mark off 7 segments of equal length. Join (1, 11) (2, 21) soon too (7, 71) where the line segments are drawn will be parallel to each other. Now the length between 1 and 2 points will be equal to 2 and 3 points and so on where each part will be 11.42cm.
7. The construction which is applicable only for dividing an angle into an even number of divisions is __________
a) Dividing an angle into 2 equal parts
b) Dividing a straight line into the desired number of equal parts
c) Dividing a straight line into proportionate equal parts
d) Dividing an angle into the equal number of divisions
View Answer
Explanation: Bisecting the given angle, further bisecting the sub-angles obtained and repeating the same procedure for all the sub-parts leaves the angles divided into many equal even parts.
8. For a rectangular hexagon, the radius of the circumscribing circle is equal to __________
a) It’s diagonal
b) It’s side
c) Half of the diagonal
d) Half of its side
View Answer
Explanation: The radius of the circle circumscribing a square is equal to the semi-length of the diagonal, and the center lies on the perpendicular bisector of its side. Logically for a hexagon, the radius of the circumscribing circle is equal to its side and the center lies on the perpendicular bisector of its side.
9. A curve traced out by a point in a straight line, which rolls without slipping along polygon or a circle is called __________
a) Cycloid
b) Loci of point
c) Conic
d) Involute
View Answer
Explanation: An involute is a curve traced out by the end of a thread unwound from a line, a polygon, or a circle, when the thread is kept taut is the unwinding process.
10. The length of the portion unwound each time is equal to the __________
a) Length of the thread
b) Length of number of sides unwound
c) The circumferential length of the portion unwound
d) The portion of the thread wounded
View Answer
Explanation: When a thread is wound over a polygon and meets its ends at a point, and one of the ends of the thread is opened to unwound, the portion of the thread unwound falls in alignment with the existing side of the polygon. This happens because the thread is kept tight during this process.
Sanfoundry Global Education & Learning Series – Engineering Drawing.
To practice all areas of Engineering Drawing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
