This set of Class 10 Maths Chapter 10 Multiple Choice Questions & Answers (MCQs) focuses on “Number of Tangents from a Point on the Circle”.
1. How many tangents can a circle have?
a) Zero
b) Infinity
c) Estimated on the value of the radius
d) Fixed for every kind of circle
View Answer
Explanation: A circle is a set of points on a plane that is equidistant from a fixed point and an infinite number of tangents can be drawn for any given circle.
2. Find the number of tangents that can be drawn for the given figure.
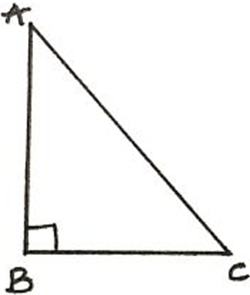
a) Estimated by using the Pythagorean theorem
b) Estimated on the value of the angle
c) Cannot be drawn
d) Estimated on the value of the diameter
View Answer
Explanation: Tangent is part of a circle. It cannot be drawn for any other figure other than a circle. Hence, tangents cannot be drawn to the given figure which is a right – angled triangle.
3. How many tangents can be drawn at one point on a circle?
a) Only one
b) Three
c) Zero
d) Two
View Answer
Explanation: A circle is a set of points on a plane that is equidistant from a fixed point and we can draw only one tangent at one point on any circle given.
4. A tangent touches a circle at a single point.
a) False
b) True
View Answer
Explanation: A line that touches/intersects a circle at exactly one point of a circle is called a tangent and an infinite number of tangents are drawn to a circle whereas secant is a line that intersects two distinct points on a circle.
5. Number of tangents passing through a circle is _____
a) 2
b) 3
c) 1
d) 0
View Answer
Explanation: A line that touches/intersects a circle at exactly one point of a circle is called a tangent and a tangent to a circle doesn’t pass through the circle.
6. What happens to the length of the chord when the chord comes closer to the center?
a) Decreases
b) Becomes an arc
c) Increases
d) Becomes a segment
View Answer
Explanation: The length of the chord of a circle increases when it comes closer and closer to the center of the circle. Hence, the longest chord becomes the diameter.
7. Find the area of the sector if the radius is 6 cm and with an angle of 60°.
a) 18.35 cm
b) 18.85 cm
c) 18.00 cm
d) 18.05 cm
View Answer
Explanation: The area of the sector = \(\frac {x^{\circ }}{360^{\circ }}\) × πr2
= \(\frac {60^{\circ }}{360^{\circ }}\) x \(\frac {22}{7}\) × 62
= 18.85 cm
8. The area of the sector is _____
a) \(\frac {x^{\circ }}{360^{\circ }}\) × πr2
b) \(\frac {x^{\circ }}{360^{\circ }}\) – πr2
c) \(\frac {x^{\circ }}{360^{\circ }}\) + πr3
d) \(\frac {x^{\circ }}{360^{\circ }}\) × πr3
View Answer
Explanation: The area of the sector is \(\frac {x^{\circ }}{360^{\circ }}\) × πr2
Where x° is the degree measure of the angle at the center and r is the radius of the circle.
9. Find the radius of a circle if 2 m is the length of the tangent, 6 m is the distance between the center of the circle the external point.
a) 7 m
b) 5 m
c) √32 m
d) √38 m
View Answer
Explanation: Length of the tangent = \(\sqrt {d^2 – r^2} \)
2 = \(\sqrt {6^2 – r^2} \)
r2 = 62 – 22
r = \(\sqrt {6^2 – 2^2} \)
r = \(\sqrt {36 – 4} \)
r = √32 m
10. Line C is secant to the circle.
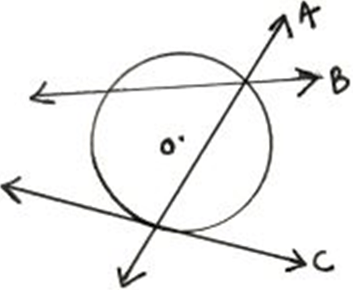
a) False
b) True
View Answer
Explanation: Tangent is a line that touches the circle at a single point. Hence, line C is a tangent, not a secant. Line A and line B are secants of the circle because they’re touching the circle at two distinct points.
Sanfoundry Global Education & Learning Series – Mathematics – Class 10.
To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 10 - Mathematics Books
- Practice Class 9 Mathematics MCQs
- Practice Class 8 Mathematics MCQs
