This set of Engineering Drawing Multiple Choice Questions & Answers (MCQs) focuses on “Centres of Gravity – 2”.
1. Which of the following statements is true in the case of the center of gravity?
a) Centre of gravity should lie inside the body
b) Centre of gravity should lie only outside the body
c) Centre of gravity lies at the center irrespective of the shape
d) Centre of gravity not necessarily lies inside the body
View Answer
Explanation: Centre of gravity is the point in the body where the resultant force acts, it may lie inside or outside the body. So, Centre of gravity not necessarily lies inside the body.
2. For the body which is symmetrical to both of its axes, where the center of gravity will be?
a) At the right side of the body
b) On one of the axes
c) At the point of intersection of the axes
d) On one of the edges
View Answer
Explanation: When a body is symmetrical about both its axes, then the center of gravity lies at the point of intersection of these axes. For example, let’s take a square, the center of gravity is the point of intersection of its diagonals as it is the symmetrical figure.
3. For the body which is symmetrical to one of its axes, where the center of gravity will be?
a) At the right side of the body
b) On the axis of symmetry
c) At the point of intersection of the axes
d) On one of the edges
View Answer
Explanation: When a body is symmetrical about one of its axes, then the center of gravity lies on the axis of symmetry. For example, let’s take a triangle, the center of gravity lies on the axis of symmetry.
4. Centre of gravity is the point in the body, through which resultant forces act.
a) False
b) True
View Answer
Explanation: A body is a collection of many particles on which force due to gravity is acted, we consider the point called the center of gravity as the point through which resultant forces act.
5. If anybody is suspended, then at _______________ the body can be balanced.
a) Center of gravity
b) Right corner
c) Centre of an edge
d) Left corner
View Answer
Explanation: A body is a collection of many particles on which force due to gravity is acted, we consider the point called the center of gravity as the point through which resultant forces act. So when a body is hung, it is balanced at the point of the center of gravity.
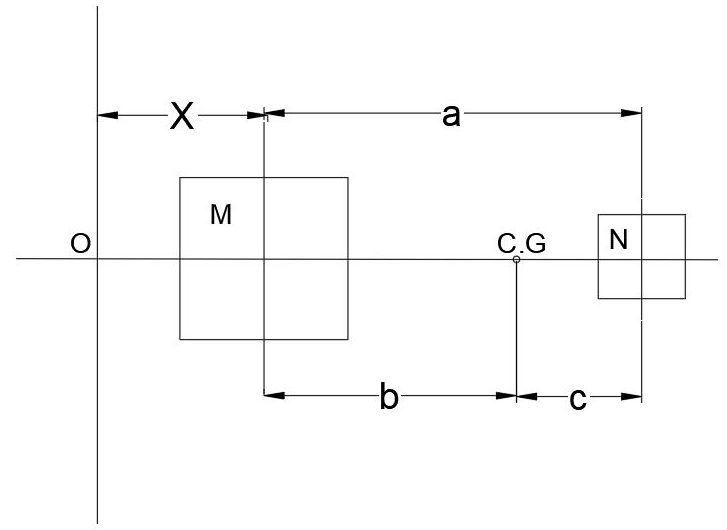
6. For the following figure, we have two square with M and N are its center of gravity, find the distance between the center of gravity from the square with center of gravity M, that is b = ________
a) Na/(M+N)
b) Na/(M-N)
c) Ma/(M+N)
d) Ma/(M-N)
View Answer
Explanation: We know the Centre of gravity for a pair of the system is C.G. = [MX+ N(a+X)]/[M+N], but we need to find the distance between the center of gravity from the square with center of gravity M, that is b. That is C.G-X = [MX+N(a+X)]/[M+N] – X. Hence b = Na/(M+N).
7. For the following figure, we have two square with M and N are its center of gravity, find the distance between the center of gravity from the square with center of gravity N, that is c = ________

a) Na/(M+N)
b) Na/(M-N)
c) Ma/(M+N)
d) Ma/(M-N)
View Answer
Explanation: We know the Centre of gravity for a pair of system is C.G. = [MX+N(a+X)]/[M+N], but we need to find the distance between the center of gravity from the square with center of gravity N, that is X+a-C.G. That is X+a-C.G = X+a-[MX+ N(a+X)]/[M+N]. Hence c = Ma/(M+N).
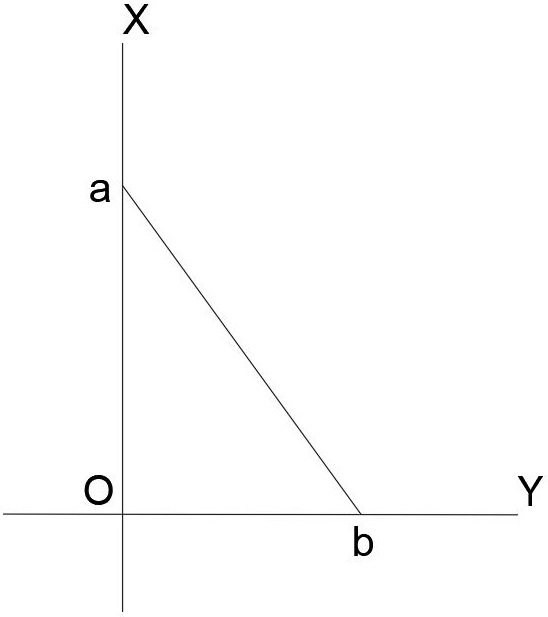
8. Find the Centre of gravity’s Y-coordinate for the following?
a) 2a/3
b) a/2
c) 3a/2
d) a/3
View Answer
Explanation: For the given triangle, the Centre of gravity lies at the intersection point of the medians. From the equilateral triangle, it is clear that it lies at one-third of the height.
9. Find the Centre of gravity’s X-coordinate for the following?

a) 2b/3
b) b/2
c) 3b/2
d) b/3
View Answer
Explanation: For the given triangle, the Centre of gravity lies at the intersection point of the medians. From the equilateral triangle, it is clear that it lies at one-third of the base.
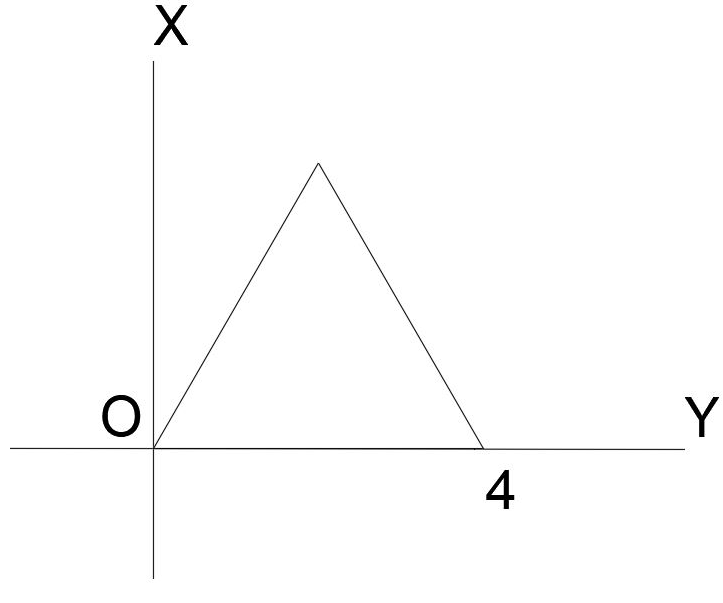
10. Find the center of gravity coordinates for the following equilateral triangle?
a) (2, 2/√3)
b) (2, 2)
c) (2/√3, 2)
d) (2/√3, 4)
View Answer
Explanation: For the equilateral triangle the medians intersect at (a/2, √3a/6), here we know the value of a = 4 units, hence the coordinates for the given equilateral triangle is (2, 2/√3).
Sanfoundry Global Education & Learning Series – Engineering Drawing.
To practice all areas of Engineering Drawing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
