This set of Basic Electrical Engineering Multiple Choice Questions & Answers (MCQs) focuses on “Kirchhoff’s Laws and Network Solution”.
1. In an AC circuit, resistance 50 Ω, inductance 0.3 H and capacitance 15 μF is connected to an AC voltage source 25 V, 50 Hz. Determine the inductive reactance in the circuit.
a) 36 ohm
b) 95 ohm
c) 125 ohm
d) 140 ohm
View Answer
Explanation: XL=2πfL f=50Hz and L=0.3H
XL=2π(50)(0.3) = 94.25 ohm.
2. In an AC circuit, resistance 50 Ω, inductance 0.3 H and capacitance 15 μF is connected to an AC voltage source 25 V, 50 Hz. Determine the capacitive reactance in the circuit.
a) 316 ohm
b) 195 ohm
c) 124 ohm
d) 212 ohm
View Answer
Explanation: XC=1/(2πfC) f=50Hz and C=15 μF
XC=1/(2π*50*15*10-6) = 212.21 ohm.
3. In an AC circuit, resistance 50 Ω, inductance 0.3 H and capacitance 15 μF is connected to an AC voltage source 25 V, 50 Hz. Determine the impedance in the circuit.
a) 110 ohm
b) 100 ohm
c) 125 ohm
d) 140 ohm
View Answer
Explanation: Z2 = R2+(XL-XC)2, XL=2πfL, XC=1/(2πfC) f=50Hz and L=0.3H and C=15 μF
XL=2π(50)(0.3)= 94.25 ohm .
XC=1/(2π*50*15*10-6) = 212.21 ohm.
Z2=502+(212.21-94.25)2=15625
Z = 125 ohm.
4. In an AC circuit, resistance 50 Ω, inductance 0.3 H and capacitance 15 μF is connected to an AC voltage source 25 V, 50 Hz. Determine the current in the circuit.
a) 0.01 A
b) 0.2 A
c) 0.02 A
d) 0.002 A
View Answer
Explanation: Z2 = R2+(XL-XC)2, XL=2πfL, XC=1/(2πfC) f=50Hz and L=0.3H and C=15 μF
XL=2π(50)(0.3)= 94.25 ohm .
XC=1/(2π*50*15*10-6) = 212.21 ohm.
Z2=502+(212.21-94.25)2=15625
Z = 125 ohm.
Current in the circuit i=V/Z=25/125=0.2 A.
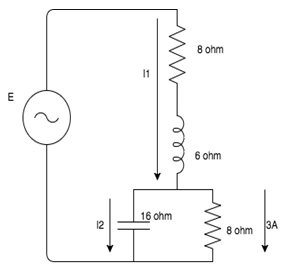
5. Find the value of the source current from the following circuit.
a) 2.54A
b) 6.67A
c) 3.35A
d) 7.65A
View Answer
Explanation: I3 =(3+j0)A
V2 =I3R=(3+j0)(8+j0)=(24+j0)V
I2=V2/Xc=(j1.5) A
I1 =I2 +I3 =(0+j1.5)+(3+j0)=(3+j1.5)A
I1=(32+1.52)1/2= 3.35A.
6. Find the value of the source voltage from the following circuit.

a) 49.2V
b) 34.6V
c) 65.2V
d) 25.6V
View Answer
Explanation: I3 =(3+j0)A
V2 =I3R=(3+j0)(8+j0)=(24+j0)V
I2=V2/Xc=(0 + j1.5) A
I1 =I2 +I3 =(0+j1.5)+(3+j0)=(3+j1.5)A
I1=(32+1.52)1/2= 3.35A.
V1 =I1(R+jXL) =(15+j30)V
E=V1 +V2 =(39+j30)V
E=(392+302)1/2= 49.2V.
7. In an AC circuit, resistance 50 Ω, inductance 0.3 H and capacitance 15 μF is connected to an AC voltage source 25 V, 50 Hz. Determine the phase difference between current and voltage.
a) 670
b) 540
c) 470
d) 770
View Answer
Explanation: XL=2πfL, XC=1/(2πfC) f=50Hz and L=0.3H and C=15 μF
XL=2π(50)(0.3) = 94.25 ohm.
XC=1/(2π*50*15*10-6) = 212.21 ohm.
tanϕ = |(XL-XC)|/R = (212.21-94.25)/50 = 2.3592
ϕ=670.
8. What value of direct current must flow through a resistor to produce the same heating power as an alternating current with a peak value of 3.5 A?
a) 1.5 A
b) 2.5 A
c) 3.5 A
d) 4.5 A
View Answer
Explanation: Power in dc circuit = Power in ac circuit (given)
IDC2R = IRMS2R
IDC=IRMS
IRMS=I0/√2 = 3.5/√2 = 2.5 A.
IDC=2.5 A.
Sanfoundry Global Education & Learning Series – Basic Electrical Engineering.
To practice all areas of Basic Electrical Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
