This set of Network Theory written test Questions & Answers focuses on “Relation between Hybrid Parameters with Short Circuit Admittance and Open Circuit Impedance Parameters”.
1. A periodic voltage v (t) = 1 + 4 sin ωt + 2 cos ωt is applied across a 1Ω resistance. The power dissipated is ____________
a) 1 W
b) 11 W
c) 21 W
d) 24.5 W
View Answer
Explanation: Given that, v (t) = 1 + 4 sin ωt + 2 cos ωt
So, Power is given by,
Power, P = \(\frac{1^2}{1} + \frac{\frac{4^2}{\sqrt{2}}}{1} + \frac{\frac{2^2}{\sqrt{2}}}{1}\)
= 11 W.
2. A constant k high pass p section has a characteristic impedance of 300 Ω at f = ∞. At f = fc, the characteristic impedance will be?
a) 0
b) ∞
c) 300 Ω
d) More than 300 Ω
View Answer
Explanation: For constant k high pass p section is given by,
Z = \(\frac{R}{\sqrt{1 – (\frac{f_d}{f})^2}}\)
At f = fd, denominator term is 0.
So, Z = infinite.
3. In the circuit given below, the current through R is 2 sin 8t. The value of R is ___________
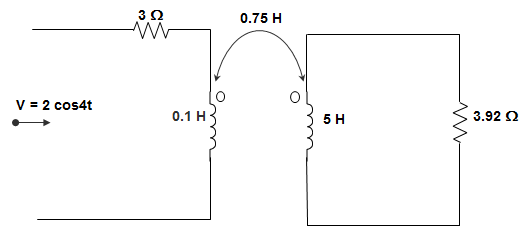
a) (0.18 + j0.72)
b) (0.46 + j1.90)
c) – (0.18 + j1.90)
d) (0.23 – 0.35 j)
View Answer
Explanation: Here, Inductor is not given, hence ignoring the inductance. Let I1 and I2 are currents in the loop then,
I1 = \(\frac{2 sin 8t}{3} \)
= 0.66 sin 8t
Again, I2 = \(\frac{-j X 4 X 0.75 I_1}{3.92-2.56j} \)
= (0.23 – 0.35j) sin 8t
So, R = (0.23 – 0.35 j).
4. For a T-network if the Short circuit admittance parameters are given as y11, y21, y12, y22, then y21 in terms of Hybrid parameters can be expressed as ________
a) y21 = \(\left(- \frac{h_{21} h_{12}}{h_{11}} + h_{22}\right)\)
b) y21 = \(\frac{h_{21}}{h_{11}} \)
c) y21 = –\(\frac{h_{12}}{h_{11}} \)
d) y21 = \(\frac{1}{h_{11}} \)
View Answer
Explanation: We know that, I1 = y11 V1 + y12 V2 ……… (1)
I2 = y21 V1 + y22 V2 ………. (2)
And, V1 = h11 I1 + h12 V2 ………. (3)
I2 = h21 I1 + h22 V2 ……….. (4)
Now, (3) and (4) can be rewritten as,
I1 = \(\frac{V_1}{h_{11}} – \frac{h_{12} V_2}{h_{11}}\) ………. (5)
And I2 = \(\frac{h_{21} V_1}{h_{11}} + \left(- \frac{h_{21} h_{12}}{h_{11}} + h_{22}\right) V_2\) ………. (6)
∴ Comparing (1), (2) and (5), (6), we get,
y11 = \(\frac{1}{h_{11}} \)
y12 = –\(\frac{h_{12}}{h_{11}} \)
y21 = \(\frac{h_{21}}{h_{11}} \)
y22 = \(\left(- \frac{h_{21} h_{12}}{h_{11}} + h_{22}\right)\).
5. For a T-network if the Open circuit impedance parameters are given as z11, z21, z12, z22, then z21 in terms of Hybrid parameters can be expressed as ________
a) z21 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
b) z21 = – \(\frac{h_{21}}{h_{22}} \)
c) z21 = \(\frac{h_{12}}{h_{22}} \)
d) z21 = \(\frac{1}{h_{22}} \)
View Answer
Explanation: We know that, V1 = z11 I1 + z12 I2 ……… (1)
V2 = z21 I1 + z22 I2 ………. (2)
And, V1 = h11 I1 + h12 V2 ………. (3)
I2 = h21 I1 + h22 V2 ……….. (4)
Now, (3) and (4) can be rewritten as,
V1 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \frac{I_1 + h_{12}}{h_{22}}I_2\) ………… (5)
And V2 = \(\frac{I_2}{h_{22}} – \frac{h_{21} I_1}{h_{22}}\) ……….. (6)
∴ Comparing (1), (2) and (5), (6), we get,
z11 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
z12 = \(\frac{h_{12}}{h_{22}} \)
z21 = – \(\frac{h_{21}}{h_{22}} \)
z22 = \(\frac{1}{h_{22}} \).
6. For a T-network if the Open circuit impedance parameters are given as z11, z21, z12, z22, then z11 in terms of Hybrid parameters can be expressed as ________
a) z11 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
b) z11 = – \(\frac{h_{21}}{h_{22}} \)
c) z11 = \(\frac{h_{12}}{h_{22}} \)
d) z11 = \(\frac{1}{h_{22}} \)
View Answer
Explanation: We know that, V1 = z11 I1 + z12 I2 ……… (1)
V2 = z21 I1 + z22 I2 ………. (2)
And, V1 = h11 I1 + h12 V2 ………. (3)
I2 = h21 I1 + h22 V2 ……….. (4)
Now, (3) and (4) can be rewritten as,
V1 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \frac{I_1 + h_{12}}{h_{22}}I_2\) ………… (5)
And V2 = \(\frac{I_2}{h_{22}} – \frac{h_{21} I_1}{h_{22}}\) ……….. (6)
∴ Comparing (1), (2) and (5), (6), we get,
z11 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
z12 = \(\frac{h_{12}}{h_{22}} \)
z21 = – \(\frac{h_{21}}{h_{22}} \)
z22 = \(\frac{1}{h_{22}} \).
7. For a T-network if the Open circuit impedance parameters are given as z11, z21, z12, z22, then z12 in terms of Hybrid parameters can be expressed as ________
a) z12 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
b) z12 = – \(\frac{h_{21}}{h_{22}} \)
c) z12 = \(\frac{h_{12}}{h_{22}} \)
d) z12 = \(\frac{1}{h_{22}} \)
View Answer
Explanation: We know that, V1 = z11 I1 + z12 I2 ……… (1)
V2 = z21 I1 + z22 I2 ………. (2)
And, V1 = h11 I1 + h12 V2 ………. (3)
I2 = h21 I1 + h22 V2 ……….. (4)
Now, (3) and (4) can be rewritten as,
V1 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \frac{I_1 + h_{12}}{h_{22}}I_2\) ………… (5)
And V2 = \(\frac{I_2}{h_{22}} – \frac{h_{21} I_1}{h_{22}}\) ……….. (6)
∴ Comparing (1), (2) and (5), (6), we get,
z11 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
z12 = \(\frac{h_{12}}{h_{22}} \)
z21 = – \(\frac{h_{21}}{h_{22}} \)
z22 = \(\frac{1}{h_{22}} \).
8. For a T-network if the Open circuit impedance parameters are given as z11, z21, z12, z22, then z22 in terms of Hybrid parameters can be expressed as ________
a) z22 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
b) z22 = – \(\frac{h_{21}}{h_{22}} \)
c) z22 = \(\frac{h_{12}}{h_{22}} \)
d) z22 = \(\frac{1}{h_{22}} \)
View Answer
Explanation: We know that, V1 = z11 I1 + z12 I2 ……… (1)
V2 = z21 I1 + z22 I2 ………. (2)
And, V1 = h11 I1 + h12 V2 ………. (3)
I2 = h21 I1 + h22 V2 ……….. (4)
Now, (3) and (4) can be rewritten as,
V1 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \frac{I_1 + h_{12}}{h_{22}}I_2\) ………… (5)
And V2 = \(\frac{I_2}{h_{22}} – \frac{h_{21} I_1}{h_{22}}\) ……….. (6)
∴ Comparing (1), (2) and (5), (6), we get,
z11 = \(\left(h_{11} – \frac{h_{21} h_{12}}{h_{22}}\right) \)
z12 = \(\frac{h_{12}}{h_{22}} \)
z21 = – \(\frac{h_{21}}{h_{22}} \)
z22 = \(\frac{1}{h_{22}} \).
9. Permeability is analogous to _____________
a) Conductivity
b) Resistivity
c) Retentivity
d) Coercivity
View Answer
Explanation: We know that resistance and reluctance are given by,
R = \(\frac{ρL}{A}\)
And Reluctance = \(\frac{L}{μA}\)
So, Permeability is analogous to conductivity.
10. A resistance and an inductance are connected in parallel and fed from 50 Hz ac mains. Each branch takes a current of 5 A. The current supplied by source is ____________
a) 10 A
b) 7.07 A
c) 5 A
d) 0 A
View Answer
Explanation: The current is given by,
|5 – j5| = \(\sqrt{5^2 + 5^2}\)
= \(\sqrt{50} = 5\sqrt{2}\) = 7.07 A.
11. A triangular Pulse of 50 V peak is applied to a capacitor of 0.1 F. The change of the capacitor and its waveform shape is ___________
a) 10 rectangular
b) 5 rectangular
c) 5 triangular
d) 10 triangular
View Answer
Explanation: We know that,
Q = CV
Or, 0.1 X 50 = 5
And it is a triangular pulse.
12. A 10 μF capacitor is charged from a 5 volt source through a resistance of 10 kΩ. The charging current offer 35 m sec. If the initial voltage on C is – 3 V is ___________
a) 0.56 mA
b) 5.6 mA
c) 6 mA
d) 5 μA
View Answer
Explanation: Initial current immediately after charging is given by,
\(\frac{V}{R} = \frac{5+3}{10000}\)
= 0.8 mA
Now, i = i0e-t/RC
= 0.8 mA x \(e^{\frac{t}{10k X 10 X 10^{-6}}}\)
= 0.8 X 10-3 X \(e^{\frac{35 X 10^{-3}}{10^{-1}}}\)
= 0.56 mA.
13. For a T-network if the Open circuit impedance parameters are given as z11, z21, z12, z22, then z11 in terms of Inverse Hybrid parameters can be expressed as ________
a) z12 = \(\frac{1}{g_{11}} \)
b) z12 = – \(\frac{g_{12}}{g_{11}} \)
c) z12 = – \(\frac{g_{21}}{g_{11}} \)
d) z12 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right)\)
View Answer
Explanation: We know that, V1 = z11 I1 + z12 I2 ……… (1)
V2 = z21 I1 + z22 I2 ………. (2)
And, I1 = g11 V1 + g12 I2 ………. (3)
V2 = g21 V1 + g22 I2 ……….. (4)
Now, (3) and (4) can be rewritten as,
V1 = \(\frac{I_1}{g_{11}} – \frac{g_{12}}{g_{11}} I_2\) ………… (5)
And V2 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right) I_2 – \frac{g_{21} I_1}{g_{11}}\) ……….. (6)
∴ Comparing (1), (2) and (5), (6), we get,
z11 = \(\frac{1}{g_{11}} \)
z12 = – \(\frac{g_{12}}{g_{11}} \)
z21 = – \(\frac{g_{21}}{g_{11}} \)
z22 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right)\).
14. For a T-network if the Open circuit impedance parameters are given as z11, z21, z12, z22, then z12 in terms of Inverse Hybrid parameters can be expressed as ________
a) z12 = \(\frac{1}{g_{11}} \)
b) z12 = – \(\frac{g_{12}}{g_{11}} \)
c) z12 = – \(\frac{g_{21}}{g_{11}} \)
d) z12 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right)\)
View Answer
Explanation: We know that, V1 = z11 I1 + z12 I2 ……… (1)
V2 = z21 I1 + z22 I2 ………. (2)
And, I1 = g11 V1 + g12 I2 ………. (3)
V2 = g21 V1 + g22 I2 ……….. (4)
Now, (3) and (4) can be rewritten as,
V1 = \(\frac{I_1}{g_{11}} – \frac{g_{12}}{g_{11}} I_2\) ………… (5)
And V2 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right) I_2 – \frac{g_{21} I_1}{g_{11}}\) ……….. (6)
∴ Comparing (1), (2) and (5), (6), we get,
z11 = \(\frac{1}{g_{11}} \)
z12 = – \(\frac{g_{12}}{g_{11}} \)
z21 = – \(\frac{g_{21}}{g_{11}} \)
z22 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right)\).
15. For a T-network if the Open circuit impedance parameters are given as z11, z21, z12, z22, then z22 in terms of Inverse Hybrid parameters can be expressed as ________
a) z22 = \(\frac{1}{g_{11}} \)
b) z22 = – \(\frac{g_{12}}{g_{11}} \)
c) z22 = – \(\frac{g_{21}}{g_{11}} \)
d) z22 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right)\)
View Answer
Explanation: We know that, V1 = z11 I1 + z12 I2 ……… (1)
V2 = z21 I1 + z22 I2 ………. (2)
And, I1 = g11 V1 + g12 I2 ………. (3)
V2 = g21 V1 + g22 I2 ……….. (4)
Now, (3) and (4) can be rewritten as,
V1 = \(\frac{I_1}{g_{11}} – \frac{g_{12}}{g_{11}} I_2\) ………… (5)
And V2 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right) I_2 – \frac{g_{21} I_1}{g_{11}}\) ……….. (6)
∴ Comparing (1), (2) and (5), (6), we get,
z11 = \(\frac{1}{g_{11}} \)
z12 = – \(\frac{g_{12}}{g_{11}} \)
z21 = – \(\frac{g_{21}}{g_{11}} \)
z22 = \(\left(g_{22} – \frac{g_{21} g_{12}}{g_{11}}\right)\).
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all written questions on Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
