This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Norton’s Theorem”.
1. Norton’s current is equal to the current passing through the ___________ circuited ___________ terminals.
a) short, input
b) short, output
c) open, output
d) open, input
View Answer
Explanation: Norton’s current is equal to the current passing through short circuited output terminals not the current through open circuited output terminals.
2. The expression of Norton’s current (IN) in the circuit shown below is?
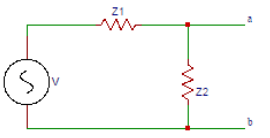
a) V/Z1
b) V/Z2
c) V(Z2/(Z1+Z2))
d) VZ1/(Z1+Z2)
View Answer
Explanation: The Norton’s equivalent form of any complex impedance circuit consists of an equivalent current source and an equivalent impedance. The expression of Norton’s current is IN = V/Z1.
3. The expression of equivalent impedance (ZN) in the circuit shown below is?

a) (Z1+Z2)/Z1
b) (Z1+Z2)/Z2
c) Z1Z2/(Z1+Z2)
d) Z1+Z2
View Answer
Explanation: The impedance between the points a and b with the source replaced by a short circuit is Norton’s equivalent impedance. The Norton’s equivalent impedance is ZN = Z1Z2/(Z1+Z2).
4. Determine Norton’s equivalent current in the circuit shown below.
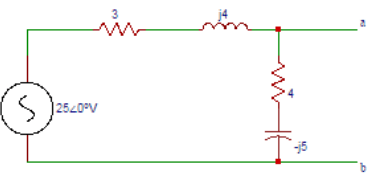
a) 5∠53.13⁰
b) 4∠53.13⁰
c) 4∠53.13⁰
d) 5∠-53.13⁰
View Answer
Explanation: The current through the terminals a and b is the Norton’s equivalent current. The Norton’s equivalent current is I = (25∠0o)/(3+j4) = 5∠-53.13⁰A.
5. The Norton’s equivalent impedance in the circuit shown below.

a) 4.53∠9.92⁰
b) 4.53∠-9.92⁰
c) 5.53∠9.92⁰
d) 5.53∠-9.92⁰
View Answer
Explanation: The Norton’s equivalent impedance is Z = (3+j4)(4-j5)/((3+j4)+(4-j5))=4.53∠9.92oΩ. The impedance between the points a and b with the source replaced by a short circuit is Norton’s equivalent impedance.
6. Determine the Norton’s impedance seen from terminals ‘ab’.
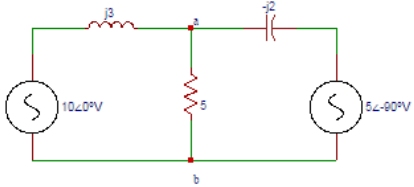
a) 6∠90⁰
b) 7∠90⁰
c) 6∠-90⁰
d) 7∠-90⁰
View Answer
Explanation: The impedance between the points a and b with the source replaced by a short circuit is Norton’s equivalent impedance. The Norton’s impedance is Zab=(j3)(-j2)/((j3)-(j2))=6∠-90oΩ.
7. Find the Norton’s current passing through ‘ab’ in the circuit shown below.

a) 4.16∠126.8⁰
b) 5.16∠126.8⁰
c) 5.16∠-126.8⁰
d) 4.16∠-126.8⁰
View Answer
Explanation: The Norton’s current is equal to the current passing through the short circuit between the points a and b. The Norton’s current is I=(10∠0o)/(3∠90o)+(5∠90o)/(2∠-90o) =4.16∠-126.8oA.
8. Find the load current in the circuit shown below.

a) 3.19∠166.61⁰
b) 3.19∠-166.61⁰
c) 4.19∠166.61⁰
d) 4.19∠-166.61⁰
View Answer
Explanation: The load current in the circuit is given by IL = I×(6∠-90o)/(5+6∠-90o) = 3.19∠-166.61oA.
9. Determine Norton’s equivalent impedance in the circuit shown below.
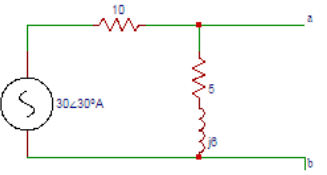
a) (5+j6) Ω
b) (5-j6) Ω
c) (6+j7) Ω
d) (6-j7) Ω
View Answer
Explanation: The impedance seen from the terminals when the source is reduced to zero is Z = (5+j6) Ω.
10. Find the Norton’s current in the circuit shown below.

a) 40∠30⁰
b) 40∠-30⁰
c) 30∠30⁰
d) 30∠-30⁰
View Answer
Explanation: The Norton’s current is equal to the current passing through the short circuit between the points a and b. So the current passing through the short circuited terminals ‘a’ and ‘b’ is I = 30∠30⁰A.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
