This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Problems Involving Coupling Coefficient”.
1. If the 3-phase balanced source in the given figure delivers 1500 W at a leading power factor of 0.844, then the value of ZL is approximately __________
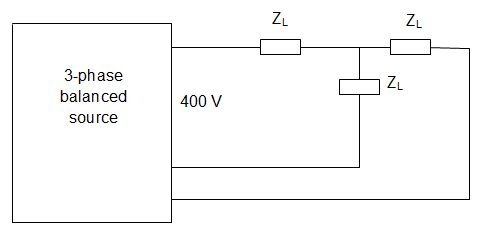
a) 90∠32.44°
b) 80∠32.44°
c) 80∠-32.44°
d) 90∠-32.44°
View Answer
Explanation: 3VP IP cosθ = 1500
Or, 3\((\frac{V_L}{\sqrt{3}}) (\frac{V_L}{\sqrt{3} Z_L})\) cos θ = 1500
Or, ZL = \(\frac{V_L^2}{1500} = \frac{400^2 (0.844)}{1500}\) = 90 Ω
And θ = ∠-arc cos(0.844)
= ∠-32.44°.
2. An RLC series circuit has a resistance R of 20Ω and a current which lags behind the applied voltage by 45°. If the voltage across the inductor is twice the voltage across the capacitor, the value of inductive resistance is ____________
a) 10 Ω
b) 20 Ω
c) 40 Ω
d) 60 Ω
View Answer
Explanation: Z = 20 + j20
V = VR = j (VL – VC)
Given, VL = 2 VC
Or, ZL = 2 ZC
Or, ZL – ZC = 20
Or, 2 ZC – ZC = 20
Or, ZC = 20 Ω
Or, ZL = 2ZC = 40 Ω.
3. In the Wheatstone bridge shown below, if the resistance in each arm is increased by 0.05%, then the value of Vout will be?
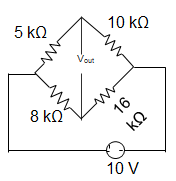
a) 50 mV
b) Zero
c) 5mV
d) 0.1mV
View Answer
Explanation: In Wheatstone bridge, balance condition is
R1R3 = R2R4
Here, R1 = 5, R2 = 10, R3 = 16, R4 = 8
And when the Wheatstone bridge is balanced then, at Vout voltage will be Zero.
4. The voltage drop across a standard resistor of 0.2 Ω is balanced at 83 cm. The magnitude of the current, if the standard cell emf of 1.53 V is balanced at 42 m is ___________
a) 13.04 A
b) 10 A
c) 14.95 A
d) 12.56 A
View Answer
Explanation: Voltage drop per unit length = \(\frac{1.53}{42}\) = 0.036 V/cm
Voltage drop across 83 cm length = 0.036 × 83 = 2.99 V
∴ Current through resistor, I = \(\frac{2.99}{0.2}\) = 14.95 A.
5. The readings of polar type potentiometer are
I = 12.4∠27.5°
V = 31.5∠38.4°
Then, Reactance of the coil will be?
a) 2.51 Ω
b) 2.56 Ω
c) 2.54 Ω
d) 2.59 Ω
View Answer
Explanation: Here, V = 31.5∠38.4°
I = 12.4∠27.5°
Z = \(\frac{31.5∠38.4°}{12.4∠27.5°}\) = 2.54∠10.9°
But Z = R + jX = 2.49 + j0.48
∴ Reactance X = 2.54 Ω.
6. The simultaneous applications of signals x (t) and y (t) to the horizontal and vertical plates respectively, of an oscilloscope, produce a vertical figure of 8 displays. If P and Q are constants and x(t) = P sin (4t + 30), then y(t) is equal to _________
a) Q sin (4t – 30)
b) Q sin (2t + 15)
c) Q sin (8t + 60)
d) Q sin (4t + 30)
View Answer
Explanation: \(\frac{f_y}{f_x} = \frac{x-peak}{y-peak}\)
Here, x-peak = 1 and y-peak = 2
∴ y(t) = Q sin (2t + 15).
7. A resistor of 10 kΩ with a tolerance of 5% is connected in parallel with 5 kΩ resistors of 10% tolerance. The tolerance limit is __________
a) 9%
b) 12.4%
c) 8.33%
d) 7.87%
View Answer
Explanation: Here, R1 and R2 are in parallel.
Then, \(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\)
Or, R = \(\frac{50}{15}\) kΩ
∴ \(\frac{△R}{R} = \frac{△R_1}{R_1^2} + \frac{△R_2}{R_2^2}\)
And △R1 = 0.5 × 103, △R2 = 0.5 × 103
∴ \(\frac{△R}{R} = \frac{10 × 10^3}{3 × 10 × 10^3} × \frac{0.5 × 10^3}{10 × 10^3} + \frac{10}{3} × \frac{10^3}{5 × 10^3} × \frac{0.5 × 10^3}{5 × 10^3}\)
= \(\frac{0.5}{30} + \frac{1}{15} = \frac{2.5}{30}\) = 8.33%.
8. A 200/1 Current Transformer (CT) is wound with 400 turns on the secondary on a toroidal core. When it carries a current of 180 A on the primary, the ratio is found to be -0.5%. If the number of secondary turns is reduced by 1, the new ratio error (in %) will be?
a) 0.0
b) -0.5
c) -1.0
d) -2.0
View Answer
Explanation: Turn compensation only alters ratio error n=400
Ratio error = -0.5% = – \(\frac{0.5}{100}\) × 400 = -2
So, Actual ratio = R = n+1 = 401
Nominal Ratio KN = \(\frac{400}{1}\) = 400
Now, if the number of turns are reduced by one, n = 399, R = 400
Ratio error = \(\frac{K_N-R}{R} = \frac{200-200}{200}\) = 0.
9. In the Two wattmeter method of measuring power in a balanced three-phase circuit, one wattmeter shows zero and the other positive maximum. The load power factor is ___________
a) 0
b) 0.5
c) 0.866
d) 1.0
View Answer
Explanation: The load power factor is = 0.5. Since at this power factor one wattmeter shows zero and the other shows a positive maximum value of power.
10. The meter constant of a single-phase, 230 V induction watt-meter is 600 rev/kW-h. The speed of the meter disc for a current of 15 A at 0.8 power factor lagging will be?
a) 30.3 rpm
b) 25.02 rpm
c) 27.6 rpm
d) 33.1 rpm
View Answer
Explanation: Meter constant = \(\frac{Number\, of\, revolution}{Energy} = \frac{600 × 230 × 15 × 0.8}{1000}\) = 1656
∴ Speed in rpm = \(\frac{1656}{60}\) = 27.6 rpm.
11. In the figure given below, a 220 V 50 Hz supplies a 3-phase balanced source. The pressure Coil (PC) and Current Coil (CC) of a watt-meter are connected to the load as shown. The watt-meter reading is _________
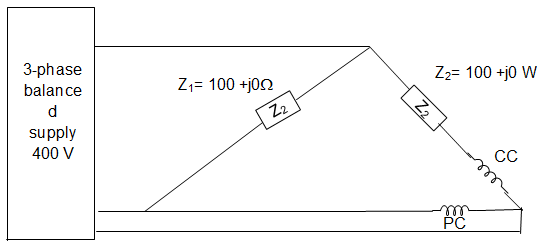
a) Zero
b) 1600 W
c) 242 W
d) 400 W
View Answer
Explanation: Watt-meter reading = Current through CC × Voltage across PC × cos (phase angle).
IBR = ICC = \(\frac{220∠120°}{100°}\) = 2.2∠120°
VYB = VPC = 220∠-120°
w = 2.2∠120° × 220∠-120° × cos 240° = – 242 W.
12. In the Owen’s bridge shown in below figure, Z1 = 200∠60°, Z2 = 400∠-90°, Z3 = 300∠0°, Z4 = 400∠30°. Then,
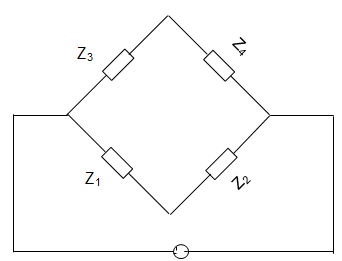
a) Bridge is balanced with given impedance values
b) Bridge can be balanced, if Z4 = 600∠60°
c) Bridge can be balanced, if Z3 = 400∠0°
d) Bridge cannot be balanced with the given configuration
View Answer
Explanation: For Bridge to be balanced, the product of impedances of the opposite arm should be equal in magnitude as well as phase angle. Here Z3 Z2 ≠ Z1 Z4 for whatever chosen value. Therefore the Bridge cannot be balanced.
13. In Maxwell’s capacitance bridge for calculating unknown inductance, the various values at balance are, R1 = 300 Ω, R2 = 700 Ω, R3 = 1500 Ω, C4 = 0.8 μF. The values of R1, L1 and Q factor, if the frequency is 1100 Hz are ____________
a) 240 Ω, 0.12 H, 3.14
b) 140 Ω, 0.168 H, 8.29
c) 140 Ω, 0.12 H, 5.92
d) 240 Ω, 0.36 H, 8.29
View Answer
Explanation: From Maxwell’s capacitance, we have
R1 = \(\frac{R_2 R_3}{R_4} = \frac{300 ×700}{1500}\) = 140 Ω
L1 = R2 R3 C4
= 300 × 700 × 0.8 × 10-6 = 0.168 H
∴ Q = \(\frac{ωL_1}{R_1}\)
= \(\frac{2 × π × 1100 × 0.168}{140}\) = 8.29.
14. In the figure below, the values of the resistance R1 and inductance L1 of a coil are to be calculated after the bridge is balanced. The values are _________________
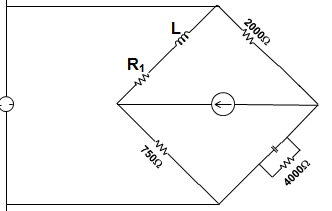
a) 375 Ω and 75 mH
b) 75 Ω and 150 mH
c) 37.5 Ω and 75 mH
d) 75 Ω and 75 mH
View Answer
Explanation: Applying the usual balance condition relation,
Z1 Z4 = Z2 Z3
We have, (R1 + jL1 ω) \(\frac{R_4/jωC_4}{R_4+1/jωC_4}\) = R2 R3
Or, R1 R4 + jL1 ωR4 = R2 R3 + j R2 R3 R4 C4 ω
∴ R1 = 2000 × \(\frac{750}{4000}\) = 375 Ω
∴ L1 = 2000 × 750 × 0.5 × 10-6 = 75 mH.
15. The four arms of an AC bridge network are as follows:
Arm AB: unknown impedance
Arm BC: standard capacitor C2 of 1000pf
Arm CD: a non-inductive resistance of R of 100 Ω in parallel to a capacitor of 0.01 μF
Arm DA: a non-inductive resistance of 1000 Ω
The supply frequency is 50 Hz and connected across terminals B and D. If the bridge is balanced with the above value, determine the value of unknown Impedance.
a) 10 kΩ
b) 100 kΩ
c) 250 kΩ
d) 20 kΩ
View Answer
Explanation: For the balance conditions,
Z1 Z3 = Z2 Z4
1000 × \(\frac{1}{jω × 1000 × 10^{-12}} = (R + jX) \frac{100}{1 + j100 × ω × 0.01 × 10^{-6}}\)
Or, \(\frac{10^{12}}{jω} = (R + jX) \left(\frac{100}{1 + jω + 10^{-6}}\right)\)
Or, \(\frac{- j 10^{10}}{ω}\) – 104 = R + jX
Comparing the real part, we get,
R = 10 kΩ.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
