This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Superposition Theorem”.
1. Superposition theorem states that the response in any element is the ____________ of the responses that can be expected to flow if each source acts independently of other sources.
a) algebraic sum
b) vector sum
c) multiplication
d) subtraction
View Answer
Explanation: The superposition theorem is used to analyze ac circuits containing more than one source. Superposition theorem states that the response in any element is the vector sum of the responses that can be expected to flow if each source acts independently of other sources.
2. Superposition theorem is valid for only linear systems.
a) true
b) false
View Answer
Explanation: Superposition theorem is valid for only linear systems. Superposition theorem is not valid for non-linear systems. In a network containing complex impedance, all quantities must be treated as complex numbers.
3. Determine the current through (2+j5) Ω impedance considering 50∠0⁰ voltage source.
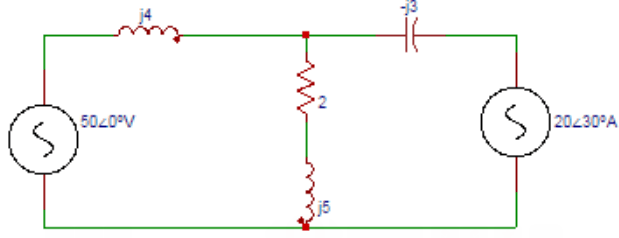
a) 6.42∠77.47⁰
b) 6.42∠-77.47⁰
c) 5.42∠77.47⁰
d) 5.42∠-77.47⁰
View Answer
Explanation: According to the superposition theorem the current due to the 50∠0o source is I1 with the current source 20∠30⁰ A short-circuited. I1 = (50∠0o)/(2+j4+j5) = 5.42∠-77.47o A.
4. Find the voltage across (2+j5) Ω impedance considering 50∠0⁰ voltage source.
a) 30.16∠-9.28⁰
b) 30.16∠9.28⁰
c) 29.16∠-9.28⁰
d) 29.16∠9.28⁰
View Answer
Explanation: Voltage across (2+j5) Ω impedance considering 50∠0⁰ voltage source is V1 = 5.42∠-77.47o (2+j5) = 29.16∠-9.28o V.
5. Find the current through (2+j5) Ω impedance considering 20∠30⁰ voltage source.
a) 8.68∠-42.53⁰
b) 8.68∠42.53⁰
c) 7.68∠42.53⁰
d) 7.68∠-42.53⁰
View Answer
Explanation: The current through (2+j5) Ω impedance considering 20∠30⁰ voltage source is I2 = 20∠30o×j4/(2+j9) = 8.68∠42.53o A.
6. Determine the voltage across (2+j5) Ω impedance considering 20∠30⁰ voltage source.
a) 45.69∠-110.72⁰
b) 45.69∠110.72⁰
c) 46.69∠-110.72⁰
d) 46.69∠110.72⁰
View Answer
Explanation: The voltage across (2+j5) Ω impedance considering 20∠30⁰ voltage source is V2 = 8.68∠42.53o (2+j5) = 46.69∠110.72⁰V.
7. Find the voltage across (2+j5) Ω impedance using Superposition theorem.
a) 40.85∠72.53⁰
b) 40.85∠-72.53⁰
c) 41.85∠72.53⁰
d) 41.85∠-72.53⁰
View Answer
Explanation: The voltage across (2+j5) Ω impedance using Superposition theorem is the sum of the voltages V1 and V2. V = V1+V2 = 29.16∠-9.28o+46.69∠110.72o=40.85∠72.53o V.
8. Determine the voltage Vab considering the source 50∠0⁰V.
a) 50∠0⁰
b) 4∠0⁰
c) 54∠0⁰
d) 46∠0⁰
View Answer
Explanation: Let source 50∠0⁰ act on the circuit and set the source 4∠0⁰A equal to zero. If the current source is zero, it becomes open-circuited. Then the voltage across ‘ab’ is 50∠0⁰.
9. Determine the voltage Vab considering the source 4∠0⁰A in the circuit shown above.
a) 46∠0⁰
b) 4∠0⁰
c) 54∠0⁰
d) 50∠0⁰
View Answer
Explanation: Set the voltage source 50∠0⁰V to zero, and is short-circuited. So, the voltage drop across ‘ab’ is zero.
10. Find the voltage Vab in the circuit shown above using Superposition theorem.
a) 4∠0⁰
b) 50∠0⁰
c) 54∠0⁰
d) 46∠0⁰
View Answer
Explanation: The total voltage is the sum of the two voltages V1 and V2 => Vab = V1+V2 = 50∠0⁰V.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Electrical Engineering Books
- Practice Electrical Engineering MCQs
- Practice Electronics & Communication Engineering MCQs
- Apply for Electrical Engineering Internship
- Apply for Electronics & Communication Engineering Internship
