This set of Network Theory Questions & Answers for Exams focuses on “Problems of Series Resonance Involving Quality Factor”.
1. A circuit tuned to a frequency of 1.5 MHz and having an effective capacitance of 150 pF. In this circuit, the current falls to 70.7 % of its resonant value. The frequency deviates from the resonant frequency by 5 kHz. Q factor is?
a) 50
b) 100
c) 150
d) 200
View Answer
Explanation: Q = \(\frac{ω}{ω1 – ω2} = \frac{f}{f2-f1}\)
Here, f = 1.5 × 106 Hz
f1 = (1.5 × 106 – 5 × 103)
f2 = (1.5 × 106 + 5 × 103)
So, f2 –f1 = 10 × 103 Hz
∴ Q = \(\frac{1.5 × 10^6}{10 × 10^3}\) = 150.
2. A circuit tuned to a frequency of 1.5 MHz and having an effective capacitance of 150 pF. In this circuit, the current falls to 70.7 % of its resonant value. The frequency deviates from the resonant frequency by 5 kHz. Effective resistance of the circuit is?
a) 2 Ω
b) 3 Ω
c) 5.5 Ω
d) 4.7 Ω
View Answer
Explanation: R = \(\frac{f2-f1}{2πf^2 L}\)
Here, f = 1.5 × 106 Hz
f1 = (1.5 × 106 – 5 × 103)
f2 = (1.5 × 106 + 5 × 103)
So, f2 – f1 = 10 × 103 Hz
∴ R = 4.7 Ω.
3. Consider a circuit consisting of two capacitors C1 and C2. Let R be the resistance and L be the inductance which are connected in series. Let Q1 and Q2 be the quality factor for the two capacitors. While measuring the Q value by the Series Connection method, the value of the Q factor is?
a) Q = \(\frac{(C_1 – C_2) Q_1 Q_2}{Q_1 C_1-Q_2 C_2}\)
b) Q = \(\frac{(C_2 – C_1) Q_1 Q_2}{Q_1 C_1-Q_2 C_2}\)
c) Q = \(\frac{(C_1 – C_2) Q_1 Q_2}{Q_2 C_2-Q_1 C_1}\)
d) Q = \(\frac{(C_2 – C_1) C_1 C_2}{Q_1 C_1-Q_2 C_2}\)
View Answer
Explanation: ωL = \(\frac{1}{ωC}\) and Q1 = \(\frac{ωL}{R} = \frac{1}{ωC_1 R}\)
XS = \(\frac{C_1 – C_2}{ωC_1 C_2}\), RS = \(\frac{Q_1 C_1 – Q_2 C_2}{ωC_1 C_2 Q_1 Q_2}\)
QX = \(\frac{X_S}{R_S} = \frac{(C_1 – C_2) Q_1 Q_2}{Q_1 C_1-Q_2 C_2}\).
4. Consider a circuit consisting of two capacitors C1 and C2. Let R be the resistance and L be the inductance which are connected in series. Let Q1 and Q2 be the quality factor for the two capacitors. While measuring the Q value by the Parallel Connection method, the value of the Q factor is?
a) Q = \(\frac{(C_1 – C_2) Q_1 Q_2}{Q_1 C_1-Q_2 C_2}\)
b) Q = \(\frac{(C_2 – C_1) Q_1 Q_2}{Q_1 C_1-Q_2 C_2}\)
c) Q = \(\frac{(C_1 – C_2) Q_1 Q_2}{Q_2 C_2-Q_1 C_1}\)
d) Q = \(\frac{(C_2 – C_1) C_1 C_2}{Q_1 C_1-Q_2 C_2}\)
View Answer
Explanation: \(\frac{1}{R_P} = \frac{ωC_1}{Q_2} – \frac{1}{RQ_1^2}\), XP = \(\frac{1}{ω(C_2-C_1)}\)
Q = \(\frac{(C_2 – C_1) Q_1 Q_2}{Q_1 C_1-Q_2 C_2}\).
5. A 50 Hz voltage is measured with a moving iron voltmeter and a rectifier type AC voltmeter connected in parallel. If the meter readings are Va and Vb respectively. Then the form factor may be estimated as?
a) \(\frac{V_a}{V_b} \)
b) \(\frac{1.11V_a}{V_b}\)
c) \(\frac{\sqrt{2} V_a}{V_b}\)
d) \(\frac{πV_a}{V_b}\)
View Answer
Explanation: Form factor of the wave = \(\frac{RMS \,value}{Mean \,value}\)
Moving iron instrument will show rms value. Rectifier voltmeter is calibrated to read rms value of sinusoidal voltage that is, with form factor of 1.11.
∴ Mean value of the applied voltage = \(\frac{V_b}{1.11}\)
∴ Form factor = \(\frac{V_a}{V_b/1.11} = \frac{1.11V_a}{V_b}\).
6. For the resonant circuit given below, the value of the quality factor of the circuit is __________
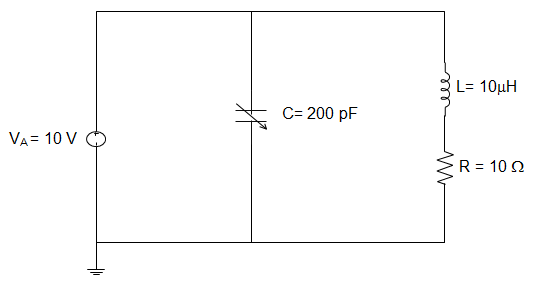
a) 5.6
b) 7.1
c) 8.912
d) 12.6
View Answer
Explanation: f = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(10 × 10^{-6})(200 × 10^{-12})}}\)
= \(\frac{1}{6.28\sqrt{2 × 10^{-15}}}\)
= \(\frac{1}{888 × 10^{-9}}\) = 1.13 MHz
Inductive Reactance, XL = 2πfL = (6.28) (1.13 × 106)(10 × 10-6)
= 70.96 Ω
∴ Q = \(\frac{X_L}{R} = \frac{70.96}{10}\) = 7.1.
7. For the series resonant circuit shown below, the value of the resonant frequency is _________
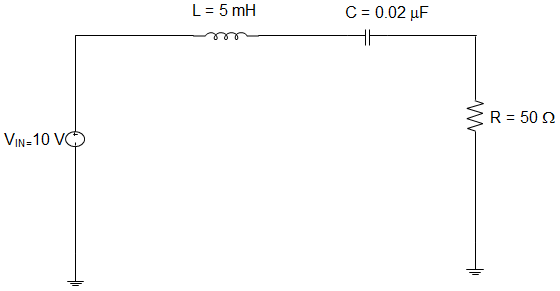
a) 36.84 kHz
b) 40.19 kHz
c) 25.28 kHz
d) 15.9 kHz
View Answer
Explanation: Resonant Frequency, FR = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(5 × 10^{-3})(0.02 × 10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{10^{-10}}}\)
= \(\frac{1}{6.28 × 10^{-5}}\) = 15.9 kHz.
8. For the series resonant circuit given below, the value of the quality factor is ___________
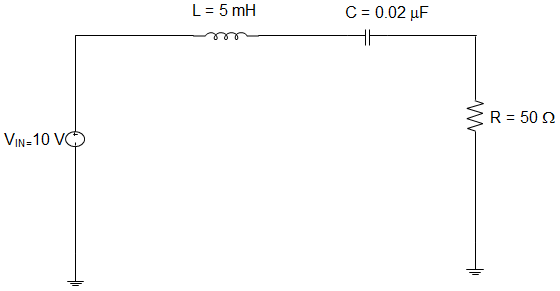
a) 15
b) 36
c) 25
d) 10
View Answer
Explanation: Resonant Frequency, FR = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(5 × 10^{-3})(0.02 × 10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{10^{-10}}}\)
= \(\frac{1}{6.28 × 10^{-5}}\) = 15.9 kHz.
Inductive Reactance, XL = 2πfL = (6.28) (15.92 × 103)(5 × 10-6)
= 0.5 kΩ
∴ Quality factor Q = \(\frac{X_L}{R} = \frac{0.5 kΩ}{50}\) = 10.
9. For the series resonant circuit given below, the bandwidth is ____________
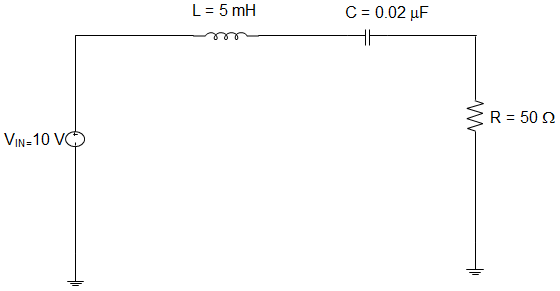
a) ±351 Hz
b) ±796 Hz
c) ±531 Hz
d) ±225 Hz
View Answer
Explanation: Resonant Frequency, FR = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(5 × 10^{-3})(0.02 × 10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{10^{-10}}}\)
= \(\frac{1}{6.28 × 10^{-5}}\) = 15.9 kHz.
Inductive Reactance, XL = 2πfL = (6.28) (15.92 × 103)(5 × 10-6)
= 0.5 kΩ
∴ Quality factor Q = \(\frac{X_L}{R} = \frac{0.5 kΩ}{50}\) = 10
∴ ∆F = \(\frac{f}{Q} = \frac{15.9 kHz}{10}\) = 1.592 kHz
∴ Bandwidth = \(\frac{∆F}{2}\) = ±796 Hz.
10. For the series circuit given below, the value of the cut-off frequencies are ____________
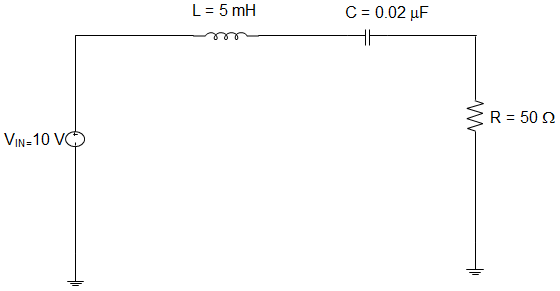
a) 78.235 kHz; 16.215 kHz
b) 13.135 kHz; 81.531 kHz
c) 16.716 kHz; 15.124 kHz
d) 50.561 kHz; 18.686 kHz
View Answer
Explanation: Resonant Frequency, FR = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(5 × 10^{-3})(0.02 × 10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{10^{-10}}}\)
= \(\frac{1}{6.28 × 10^{-5}}\) = 15.9 kHz.
Inductive Reactance, XL = 2πfL = (6.28) (15.92 × 103)(5 × 10-6)
= 0.5 kΩ
∴ Quality factor Q = \(\frac{X_L}{R} = \frac{0.5 kΩ}{50}\) = 10
∴ ∆F = \(\frac{f}{Q} = \frac{15.9 kHz}{10}\) = 1.592 kHz
∴ Bandwidth = \(\frac{∆F}{2}\) = ±796 Hz.
Therefore, f2 = f + \(\frac{∆F}{2}\) = 16.716 kHz and f1 = f – \(\frac{∆F}{2}\) = 15.124 kHz.
11. In a series resonance type BPF, C = 1.8 pf, L = 25 mH, RF = 52 Ω and RL = 9 kΩ. The Resonant frequency f is __________
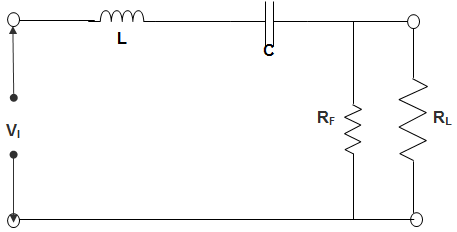
a) 75.1 kHz
b) 751 kHz
c) 575 kHz
d) 57.5 kHz
View Answer
Explanation: f = \(\frac{1}{2π\sqrt{LC}} = \frac{1}{2π\sqrt{0.025×1.8×10^{-12}}}\)
= \(\frac{1}{2π} × \frac{10^6}{\sqrt{0.45}}\)
= \(\frac{1}{2π} × \frac{10^6}{0.67}\)
= 751000
∴ f = 751 kHz.
12. In a series resonance type BPF, C = 1.8 pf, L = 25 mH, RF = 52 Ω and RL = 9 kΩ. The Bandwidth is ___________
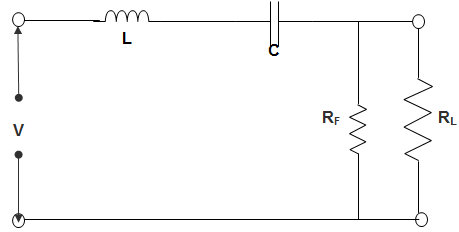
a) 331 kHz
b) 575 kHz
c) 331 Hz
d) 575 Hz
View Answer
Explanation: R = \(\frac{R_f×R_L}{R_f+R_L}\) ≈ 52 Ω
∴ Qfactor = \(\frac{ω_r L}{R} = \frac{2π×751×25×10^{-3}}{52} \)
= \(\frac{π×37580}{52}\) = 2270
Now, BW = \(\frac{f_r}{Q} = \frac{751 × 10^3}{2270}\)
∴ BW = 331 Hz.
13. A 50 μF capacitor, when connected in series with a coil having a resistance of 40Ω, resonates at 1000 Hz. The inductance of the coil for the resonant circuit is ____________
a) 2.5 mH
b) 1.2 mH
c) 0.5 mH
d) 0.1 mH
View Answer
Explanation: At resonance, XL = XC
Or, 2πfL = \(\frac{1}{2πfC} \)
∴ L = \(\frac{1}{4π^2 f^2 C} \)
= \(\frac{1}{4π^2 × (1000)^2 × 50 × 10^{-6}} \)
= \(\frac{1}{39.46×50} \)
= 0.0005
So, L = 0.5 mH.
14. A coil (which can be modelled as a series RL circuit) has been designed for a high Quality Factor (Q) performance. The voltage is rated at and a specified frequency. If the frequency of operation is increased 10 times and the coil is operated at the same rated voltage. The new value of Q factor and the active power P will be?
a) P is doubled and Q is halved
b) P is halved and Q is doubled
c) P remains constant and Q is doubled
d) P decreases 100 times and Q is increased 10 times
View Answer
Explanation: ω2 L = 10 ω1 LR will remain constant
∴ Q2 = \(\frac{10 ω_1 L}{R}\) = 10 Q1
That is Q is increased 10 times.
Now, I1 = \(\frac{V}{ω_1 L} \)
For a high Q coil, ωL >> R,
I2 = \(\frac{V}{10 ω_1 L} = \frac{I_1}{10}\)
∴ P2 = R \((\frac{I_1}{10})^2 = \frac{P_1}{100}\)
Thus, P decreases 100 times and Q is increased 10 times.
15. A 50 Hz, bar primary CT has a secondary with 800 turns. The secondary supplies 7 A current into a purely resistive burden of 2 Ω. The magnetizing ampere-turns are 300. The phase angle is?
a) 3.1°
b) 85.4°
c) 94.6°
d) 175.4°
View Answer
Explanation: Secondary burden is purely resistive and the resistance of burden is equal to the resistance of the secondary winding; the resistance of secondary winding = 1Ω. The voltage induced in secondary × resistance of secondary winding = 7 × 2 = 14V. Secondary power factor is unity as the load is purely resistive. The loss component of no-load current is to be neglected i.e. Ie = 0. IM = 300 A.
Secondary winding current IS = 7 A
Reflected secondary winding current = n IS = 5600 A
∴ tan θ = \(\frac{I_M}{nI_S} \). So, θ = 3.1°.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Network Theory Books
- Check Electrical Engineering Books
- Practice Electrical Engineering MCQs
- Apply for Electrical Engineering Internship
- Check Electronics & Communication Engineering Books
