Parallel Resonance Problems Questions and Answers

This set of Network Theory Questions & Answers for Exams focuses on “Problems of Parallel Resonance Involving Quality Factor”.

1. For the parallel resonant circuit shown below, the value of the resonant frequency is _________

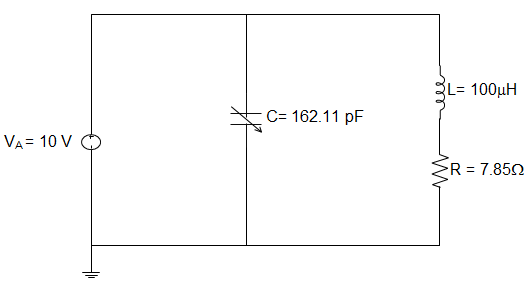
a) 1.25 MHz
b) 2.5 MHz
c) 5 MHz
d) 1.5 MHz
View Answer

Answer: a
Explanation: Resonant Frequency, F_R = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(100×10^{-6})(162.11×10^{-12})}}\)
= \(\frac{1}{6.28\sqrt{1.621×10^{-14}}}\)
= \(\frac{1}{799×10^{-9}}\) = 1.25 MHz.

2. For the parallel resonant circuit given below, the value of the inductive and capacitive reactance is _________

a) X_L = 654.289 Ω; X_C = 458.216 Ω
b) X_L = 985.457 Ω; X_C = 875.245 Ω
c) X_L = 785.394 Ω; X_C = 785.417 Ω
d) X_L = 125.354 Ω; X_C = 657.215 Ω
View Answer

Answer: c
Explanation: Resonant Frequency, f = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(100×10^{-6})(162.11×10^{-12})}}\)
= \(\frac{1}{6.28\sqrt{1.621×10^{-14}}}\)
= \(\frac{1}{799×10^{-9}}\) = 1.25 MHz.
Inductive Reactance, X_L = 2πfL = (6.28) (1.25×10⁶)(100×10^-6)
= 785.394 Ω
Capacitive Reactance, X_C = \(\frac{1}{2πfC} = \frac{1}{(6.28)(1.25×10^6)(162.11×10^{-12})}\)
= \(\frac{1}{1.273×10^{-3}}\) = 785.417 Ω.

3. For the parallel resonant circuit given below, the current through the capacitor and inductor are _________

a) I_C = 10.892 mA; I_L = 12.732 mA
b) I_C = 12.732 mA; I_L = 10.892 mA
c) I_C = 10.892 mA; I_L = 10.892 mA
d) I_C = 12.732 mA; I_L = 12.732 mA
View Answer

Answer: d
Explanation: Resonant Frequency, f = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(100×10^{-6})(162.11×10^{-12})}}\)
= \(\frac{1}{6.28\sqrt{1.621×10^{-14}}}\)
= \(\frac{1}{799×10^{-9}}\) = 1.25 MHz.
Inductive Reactance, X_L = 2πfL = (6.28) (1.25×10⁶)(100×10^-6)
= 785.394 Ω
Capacitive Reactance, X_C = \(\frac{1}{2πfC} = \frac{1}{(6.28)(1.25×10^6)(162.11×10^{-12})}\)
= \(\frac{1}{1.273×10^{-3}}\) = 785.417 Ω.
I_C = \(\frac{V_A}{X_C} \)
= \(\frac{10}{785.417} \) = 12.732 mA
I_L = \(\frac{V_A}{X_L} \)
= \(\frac{10}{785.394} \) = 12.732 mA.

4. For the parallel resonant circuit given below, the value of the equivalent impedance of the circuit is ________

a) 56.48 kΩ
b) 78.58 kΩ
c) 89.12 kΩ
d) 26.35 kΩ
View Answer

Answer: b
Explanation: f = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(100×10^{-6})(162.11×10^{-12})}}\)
= \(\frac{1}{6.28\sqrt{1.621×10^{-14}}}\)
= \(\frac{1}{799×10^{-9}}\) = 1.25 MHz.
Inductive Reactance, X_L = 2πfL = (6.28) (1.25×10⁶)(100×10^-6)
= 785.394 Ω
Q = \(\frac{X_L}{R} = \frac{785.394}{7.85}\) = 100.05
∴ Z_EQ = QX_L = (100.05)(785.394) = 78.58 kΩ.

5. For the parallel resonant circuit, the bandwidth of the circuit is ____________

a) ±6.25 kHz
b) ±8.56 kHz
c) ±10.35 kHz
d) ±6.37 kHz
View Answer

Answer: a
Explanation: Resonant Frequency, f = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(100×10^{-6})(162.11×10^{-12})}}\)
= \(\frac{1}{6.28\sqrt{1.621×10^{-14}}}\)
= \(\frac{1}{799×10^{-9}}\) = 1.25 MHz.
Inductive Reactance, X_L = 2πfL = (6.28) (1.25×10⁶)(100×10^-6)
= 785.394 Ω
Q = \(\frac{X_L}{R} = \frac{785.394}{7.85}\) = 100.05
∴ ∆F = \(\frac{f}{Q} = \frac{1.25 × 10^6}{100.05}\) = 12.5 kHz
Hence, bandwidth = \(\frac{∆F}{2}\) = 6.25 kHz.

Subscribe Now: Network Theory Newsletter | Important Subjects Newsletters

6. For the parallel resonant circuit given below, the cut-off frequencies are ____________

a) ∆f₁ = 2.389 MHz; ∆f₂ = 441.124 MHz
b) ∆f₁ = 1.256 MHz; ∆f₂ = 1.244 MHz
c) ∆f₁ = 5.658 MHz; ∆f₂ = 6.282 MHz
d) ∆f₁ = 3.656 MHz; ∆f₂ = 8.596 MHz
View Answer

Answer: b
Explanation: Resonant Frequency, f = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(100×10^{-6})(162.11×10^{-12})}}\)
= \(\frac{1}{6.28\sqrt{1.621×10^{-14}}}\)
= \(\frac{1}{799×10^{-9}}\) = 1.25 MHz.
Inductive Reactance, X_L = 2πfL = (6.28) (1.25×10⁶)(100×10^-6)
= 785.394 Ω
Q = \(\frac{X_L}{R} = \frac{785.394}{7.85}\) = 100.05
∴ ∆F = \(\frac{f}{Q} = \frac{1.25 × 10^6}{100.05}\) = 12.5 kHz
Hence, bandwidth = \(\frac{∆F}{2}\) = 6.25 kHz
∴ ∆f₁ = f + \(\frac{∆F}{2}\) = 1.25 MHz + 6.25 kHz = 1.256 MHz
∴ ∆f₁ = f – \(\frac{∆F}{2}\) = 1.25 MHz – 6.25 kHz = 1.244 MHz.

7. For the series resonant circuit shown below, the value of the resonant frequency is _________

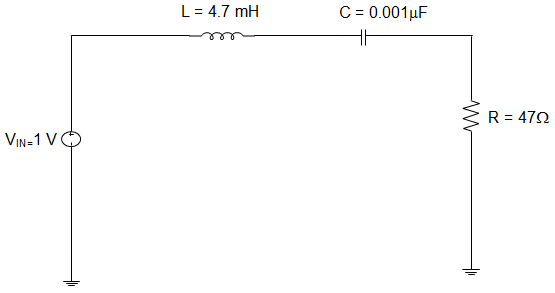
a) 10.262 kHz
b) 44.631 kHz
c) 50.288 kHz
d) 73.412 kHz
View Answer

Answer: d
Explanation: Resonant Frequency, F_R = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(4.7×10^{-3})(0.001×10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{4.7×10^{-12}}}\)
= \(\frac{1}{1.362×10^{-5}}\) = 73.412 kHz.

8. For the series resonant circuit given below, the value of the inductive and capacitive reactance is _________

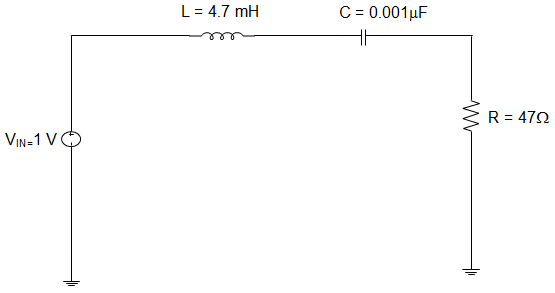
a) X_L = 5.826 kΩ; X_C = 5.826 kΩ
b) X_L = 2.168 kΩ; X_C = 2.168 kΩ
c) X_L = 6.282 kΩ; X_C = 6.282 kΩ
d) X_L = 10.682 kΩ; X_C = 10.682 kΩ
View Answer

9. For the series resonant circuit given below, the value of the equivalent impedance of the circuit is ________

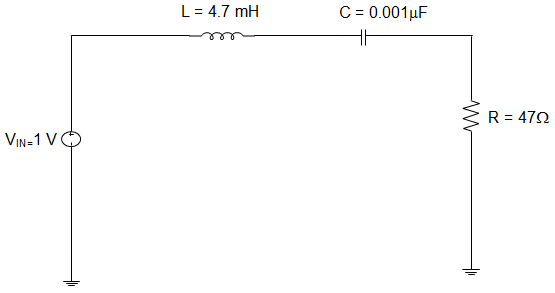
a) 55 Ω
b) 47 Ω
c) 64 Ω
d) 10 Ω
View Answer

Answer: b
Explanation: Resonant Frequency, \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(4.7×10^{-3})(0.001×10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{4.7×10^{-12}}}\)
= \(\frac{1}{1.362×10^{-5}}\) = 73.412 kHz
Inductive Reactance, X_L = 2πfL = (6.28) (73.142 × 10³)(4.7 × 10^-6)
= 2.168 kΩ
Capacitive Reactance, X_C = \(\frac{1}{2πfC} = \frac{1}{(6.28)(73.142×10^3)(0.001×10^{-6})}\)
= \(\frac{1}{4.613×10^{-4}}\) = 2.168 kΩ
We see that, X_C = X_L are equal, along with being 180° out of phase.
Hence the net reactance is zero and the total impedance equal to the resistor.
∴ Z_EQ = R = 47 Ω.

10. For the series resonant circuit given below, the value of the total current flowing through the circuit is ____________

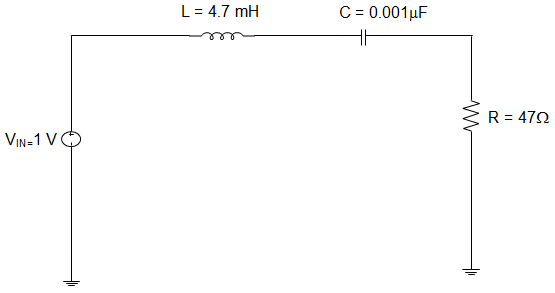
a) 7.521 mA
b) 6.327 mA
c) 2.168 mA
d) 9.136 mA
View Answer

Answer: a
Explanation: Resonant Frequency, \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(4.7×10^{-3})(0.001×10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{4.7×10^{-12}}}\)
= \(\frac{1}{1.362×10^{-5}}\) = 73.412 kHz
Inductive Reactance, X_L = 2πfL = (6.28) (73.142 × 10³)(4.7 × 10^-6)
= 2.168 kΩ
Capacitive Reactance, X_C = \(\frac{1}{2πfC} = \frac{1}{(6.28)(73.142×10^3)(0.001×10^{-6})}\)
= \(\frac{1}{4.613×10^{-4}}\) = 2.168 kΩ
Z_EQ = R = 47 Ω
I_T = \(\frac{V_{in}}{Z_{EQ}} = \frac{V_{in}}{R} = \frac{0.3535}{47}\) = 7.521 mA.

11. For the series circuit given below, the value of the voltage across the capacitor and inductor are _____________

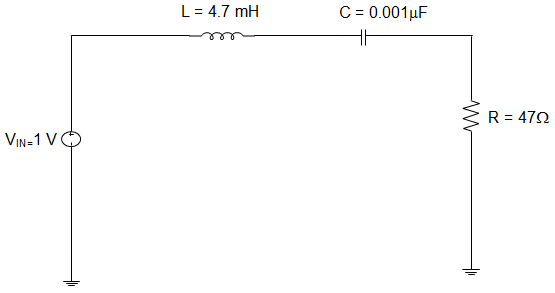
a) V_C = 16.306 V; V_L = 16.306 V
b) V_C = 11.268 V; V_L = 11.268 V
c) V_C = 16.306 V; V_L = 16.306 V
d) V_C = 14.441 V; V_L = 14.441 V
View Answer

Answer: c
Explanation: Resonant Frequency, \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(4.7×10^{-3})(0.001×10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{4.7×10^{-12}}}\)
= \(\frac{1}{1.362×10^{-5}}\) = 73.412 kHz
Inductive Reactance, X_L = 2πfL = (6.28) (73.142 × 10³)(4.7 × 10^-6)
= 2.168 kΩ
Capacitive Reactance, X_C = \(\frac{1}{2πfC} = \frac{1}{(6.28)(73.142×10^3)(0.001×10^{-6})}\)
= \(\frac{1}{4.613×10^{-4}}\) = 2.168 kΩ
Z_EQ = R = 47 Ω
I_T = \(\frac{V_{in}}{Z_{EQ}} = \frac{V_{in}}{R} = \frac{0.3535}{47}\) = 7.521 mA
∴ Voltage across the capacitor, V_C = X_CI_T = (2.168 kΩ)(7.521 mA) = 16.306 V
∴ Voltage across the inductor, V_L = X_LI_T = (2.168 kΩ)(7.521 mA) = 16.306 V.

12. For the series resonant circuit given below, the value of the quality factor is ___________

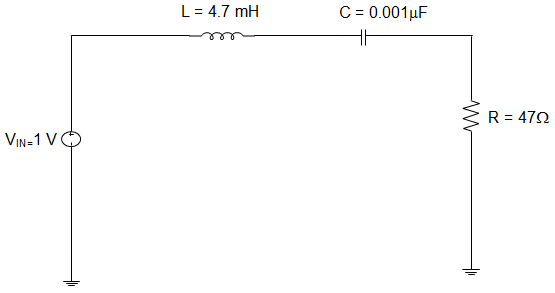
a) 35.156
b) 56.118
c) 50.294
d) 46.128
View Answer

Answer: d
Explanation: Resonant Frequency, \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{6.28\sqrt{(4.7×10^{-3})(0.001×10^{-6})}}\)
= \(\frac{1}{6.28\sqrt{4.7×10^{-12}}}\)
= \(\frac{1}{1.362×10^{-5}}\) = 73.412 kHz
Inductive Reactance, X_L = 2πfL = (6.28) (73.142 × 10³)(4.7 × 10^-6)
= 2.168 kΩ
Quality factor Q = \(\frac{X_L}{R} = \frac{2.168 kΩ}{47}\) = 46.128.

13. For a parallel RLC circuit, the incorrect statement among the following is _____________
a) The bandwidth of the circuit decreases if R is increased
b) The bandwidth of the circuit remains same if L is increased
c) At resonance, input impedance is a real quantity
d) At resonance, the magnitude of input impedance attains its minimum value
View Answer

Answer: d
Explanation: BW = 1/RC
It is clear that the bandwidth of a parallel RLC circuit is independent of L and decreases if R is increased.
At resonance, imaginary part of input impedance is zero. Hence, at resonance input impedance is a real quantity.
In parallel RLC circuit, the admittance is minimum, at resonance. Hence the magnitude of input impedance attains its maximum value at resonance.

14. A circuit excited by voltage V has a resistance R which is in series with an inductor and capacitor, which are connected in parallel. The voltage across the resistor at the resonant frequency is ___________
a) 0
b) \(\frac{V}{2}\)
c) \(\frac{V}{3}\)
d) V
View Answer

Answer: a
Explanation: Dynamic resistance of the tank circuit, Z_DY = L/(R_LC)
But given that R_L = 0
So, Z_DY = L/(0X_C) = ∞
Therefore current through circuit, I = \(\frac{V}{∞}\) = 0
∴ V_D = 0.

15. For the circuit given below, the nature of the circuit is ____________

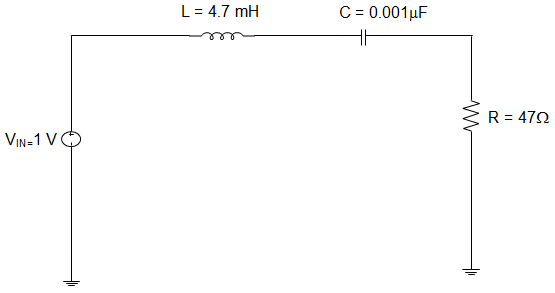
a) Inductive
b) Capacitive
c) Resistive
d) Both inductive as well as capacitive
View Answer

Answer: c
Explanation: θ = 0° since X_L and X_C are cancelling, which means at resonance the circuit is purely resistive.

Sanfoundry Global Education & Learning Series – Network Theory.

To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Network Theory Questions and Answers – Problems of Series Resonance Involving Frequency Response of Series Resonant Circuit

» Next - Network Theory Questions and Answers – Advanced Problems on Resonance

Related Posts:

Practice Electronics & Communication Engineering MCQs
Apply for Electrical Engineering Internship
Practice Electrical Engineering MCQs
Check Electronics & Communication Engineering Books
Check Network Theory Books

Recommended Articles: