This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Mesh Analysis”.
1. If there are M branch currents, then we can write ___________ number of independent equations.
a) M-2
b) M-1
c) M
d) M+1
View Answer
Explanation: If there are M branch currents, then we can write M number of independent equations. Number of independent equations = M.
2. If there are M meshes, B branches and N nodes including reference node, the number of mesh currents is given as M=?
a) B + (N+1)
b) B + (N-1)
c) B-(N+1)
d) B-(N-1)
View Answer
Explanation: If there are M meshes, B branches and N nodes including reference node, the number of mesh currents is given as M = B-(N-1).
3. Determine the current I1 in the circuit shown below using mesh analysis.
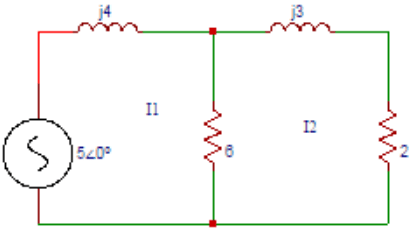
a) 0.955∠-69.5⁰
b) 0.855∠-69.5⁰
c) 0.755∠-69.5⁰
d) 0.655∠-69.5⁰
View Answer
Explanation: The equation for loop 1 is I1(j4) + 6(I1-I2) = 5∠0⁰. The equation for loop 2 is 6(I1-I2) + (j3) I2 + (2) I2 = 0. Solving the above equations, I1 = 0.855∠-69.5⁰.
4. In the circuit shown below. Find the current I2.

a) 0.5∠-90⁰
b) 0.6∠-90⁰
c) 0.7∠-90⁰
d) 0.8∠-90⁰
View Answer
Explanation: The equation for loop 1 is I1(j4) + 6(I1-I2) = 5∠0⁰. The equation for loop 2 is 6(I1-I2) + (j3) I2 + (2) I2 = 0. Solving the above equations, I2 = 0.6∠-90⁰.
5. Find Z11, Z12, Z13 obtained from the mesh equations in the circuit shown below.
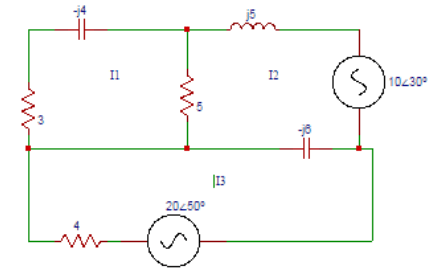
a) (8+j4) Ω, 5 Ω, 0Ω
b) (8-j4) Ω, 5 Ω, 0Ω
c) (8+j4) Ω, – 5 Ω, 0Ω
d) (8-j4) Ω, -5 Ω, 0Ω
View Answer
Explanation: Z11= self impedance of loop 1 = (5 + 3 – j4) Ω. Z12 = Impedance common to both loop 1 and loop2 = -5Ω. Z13 = No common impedance between loop1 and loop 3 = 0Ω.
6. Determine Z21, Z22, Z23 in the circuit shown below.

a) 5Ω, (5-j1) Ω, j6 Ω
b) -5Ω, (5-j1) Ω, j6 Ω
c) -5Ω, (5+j1) Ω, j6 Ω
d) -5Ω, (5-j1) Ω, – j6 Ω
View Answer
Explanation: Z21 = common impedance to loop 1 and loop 2 = -5 Ω. Z22 = self impedance of loop2 = (5+j5-j6) Ω. Z23 = common impedance between loop2 and loop 3 = – (-j6) Ω.
7. Find Z31, Z32, Z33 in the circuit shown below.

a) 0Ω, j6Ω, (4-j6) Ω
b) 0Ω, -j6Ω, (4+j6) Ω
c) 0Ω, -j6Ω, (4-j6) Ω
d) 0Ω, j6Ω, (4+j6) Ω
View Answer
Explanation: Z31 = common impedance to loop 3 and loop 1 = 0 Ω. Z32 = common impedance between loop3 and loop 2 = – (-j6) Ω. Z33 = self impedance of loop 3 = (4-j6) Ω.
8. Find the values of Z11, Z22, Z33 in the circuit shown below.
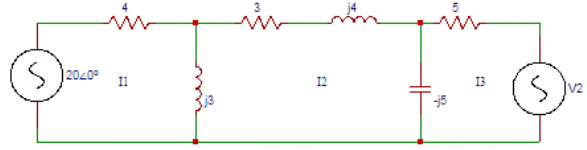
a) (4+j3) Ω, (3-j2) Ω, (5-j5) Ω
b) (4+j3) Ω, (3+j2) Ω, (5-j5) Ω
c) (4-j3) Ω, (3-j2) Ω, (5-j5) Ω
d) (4+j3) Ω, (3-j2) Ω, (5+j5 ) Ω
View Answer
Explanation: Z11 = self impedance of loop 1 = (4 + j3) Ω. Z22 = self impedance of loop2 = (j3+3+j4-j5) Ω. Z33 = self impedance of loop 3 = (-j5+5) Ω.
9. Find the common impedances Z12, Z13, Z21, Z23, Z31, Z32 respectively in the circuit shown below.

a) -j3Ω, 0Ω, -j3Ω, j5Ω, 0Ω, j5Ω
b) j3Ω, 0Ω, -j3Ω, j5Ω, 0Ω, j5Ω
c) j3Ω, 0Ω, -j3Ω, j5Ω, 0Ω,- j5Ω
d) j3Ω, 0Ω, -j3Ω, -j5Ω, 0Ω, j5Ω
View Answer
Explanation: The common impedances Z12 and Z21 are Z12 = Z21 = -j3Ω. The common impedances Z13 and Z31 are Z13 = Z31 = 0Ω. The common impedances Z23 and Z32 are Z23 = Z32 = j5Ω.
10. Find the value V2 in the circuit shown below if the current through (3+j4) Ω is zero.

a) 16∠-262⁰
b) 17∠-262⁰
c) 18∠-262⁰
d) 19∠-262⁰
View Answer
Explanation: The three loop equations are (4+j3)I1 – (j3)I2 = 20∠0⁰. (-j3)I1 + (3+j2)I2 + (j5)I3 = 0. (j5)I2 + (5-j5)I3 = -V2. The current through (3+j4) Ω is zero, I2 = ∆2/∆ = 0
4+j3 20∠0⁰ 0
∆2 = | -j3 0 j5 |
0 -V2 5-j5On solving, V2 = 17∠-262⁰.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
