This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Series-Parallel Interconnection of Two Port Network”.
1. If the diameter of a wire is doubled, the current carrying capacity of the wire is ___________
a) Half
b) Twice
c) Four times
d) One-fourth
View Answer
Explanation: Since diameter is doubled, area of cross-section becomes four times. Current carrying capacity is proportional to area of cross-section.
2. Consider an RL series circuit having resistance R = 3 Ω, inductance L = 3 H and is excited by 6V. The current after a long time after closing of switch is ____________
a) 1 A
b) 2 A
c) 0 A
d) Infinity
View Answer
Explanation: At t = ∞ the circuit has effectively two 6Ω resistances in parallel.
So, REQ = \(\frac{6 X 6}{6 + 6}\)
= \(\frac{36}{12}\) = 3 Ω
Given voltage = 6 V
So, current = 2 A.
3. The energy stored in a coil is 108 J. The power dissipated instantaneously across the blades of switch after it is opened in 10 ms is ____________
a) 108 W
b) 1080 W
c) 10800 W
d) 108000 W
View Answer
Explanation: Power dissipated instantaneously across the blades of the switch is given by,
Power, P = \(\frac{Energy}{Time}\)
Given that, Energy = 108 J and time = 10 X 10-3
So, P = \(\frac{108}{10 X 10^{-3}}\) = 10800 W.
4. A parallel RLC circuit with R1 = 20, L1 = \(\frac{1}{100}\) and C1 = \(\frac{1}{200}\) is scaled giving R2 = 104, L2 = 10-4 and C2, the value of C2 is ___________
a) 0.10 nF
b) 0.3 nF
c) 0.2 nF
d) 0.4 nF
View Answer
Explanation: K1 = \(\frac{R_2}{R_1}\)
= \(\frac{10^4}{20}\) = 5 X 102 = 500 Ω
And \(\frac{L_1}{L_2} = \frac{kω}{k_1}\)
Or, \(\frac{kω}{k_1} = \frac{L_1}{L_2} X k_1\)
Or, \(\frac{10^{-2}}{10^{-4} X 5 X 10^2}\) = 5 X 104
Or, C2 = \(\frac{C_1}{kω.k_1} = \frac{0.5 X 10^{-2}}{5 X 10^4 X 500}\)
= 0.02 X 10-8 = 0.2 nF.
5. Barletts Bisection Theorem is applicable to ___________
a) Unsymmetrical networks
b) Symmetrical networks
c) Both unsymmetrical and symmetrical networks
d) Neither to unsymmetrical nor to symmetrical networks
View Answer
Explanation: A symmetrical network can be split into two halves. So the z parameters of the network are symmetrical as well as reciprocal of each other. Hence Barletts Bisection Theorem is applicable to Symmetrical networks.
6. The Thevenin’s equivalent of a network is a 10 V source in series with 2 Ω resistances. If a 3 Ω resistance is connected across the Thevenin’s equivalent is _____________
a) 10 V in series with 1.2 Ω resistance
b) 6 V in series with 1.2 Ω resistance
c) 10 V in series with 5 Ω resistance
d) 6 V in series with 5 Ω resistance
View Answer
Explanation: The Thevenin equivalent voltage is given by,
VTH = \(\frac{10 X 3}{5}\)
= 6 V
And the Thevenin equivalent Resistance is given by,
RTH = \(\frac{3 X 2}{5}\) = 1.2 Ω.
7. A magnetic circuit has an iron length of 100 cm and air gap length 10 cm. If μr = 200 then which of the following is true?
a) Mmf for iron and air gap are equal
b) Mmf for iron is much less than that for air gap
c) Mmf for iron is much more than that for air gap
d) Mmf for iron and air gap are not equal
View Answer
Explanation: We know that, MMF for air = \(\frac{B}{4π X 10^{-7}}\) X 10
Where B is the magnetic field intensity.
Also, MMF for iron = \(\frac{B X 100}{200(4π X 10^{-7})}\)
= \(\frac{B X 0.5}{4π X 10^{-7}}\).
8. Two coils X and Y have self-inductances of 5 mH and 10 mH and mutual inductance of 3 mH. If the current in coils X change at a steady rate of 100 A/s, the emf induced in coil Y is ____________
a) 0.3 V
b) 0.5 V
c) 1 V
d) 1.5 V
View Answer
Explanation: The emf is given by,
V = M\(\frac{di}{dt}\)
= \(\frac{3}{1000}\) X 100 = 0.3 V
Hence, the emf induced in coil Y is given by 0.3 V.
9. A 50 Hz current has an amplitude of 25 A. The rate of change of current at t = 0.005 after i = 0 and is increasing is ____________
a) 2221.44 A/s
b) 0
c) -2221.44 A/s
d) -3141.6 A/s
View Answer
Explanation: The current i (t) is given by,
i = 25 sin 314.16 t and \(\frac{di}{dt}\) = 250 X 314.16 cosωt
Now, at t = 0.005, I = 25 X 314.16 cos (314.16 X 0.005)
= 0.
10. Consider a series RL circuit in which current 12 A is flowing through R and current 16 A is flowing through L. The current supplied by the sinusoidal current source I is ____________
a) 28 A
b) 4 A
c) 20 A
d) Cannot be determined
View Answer
Explanation: Current I (t) is given by,
I (t) = \(\sqrt{16^2 + 12^2}\)
= \(\sqrt{256+144}\)
= \(\sqrt{400}\)
= 20 A.
11. Consider a circuit having resistances 16 Ω and 30 Ωis excited by a voltage V. A variable resistance R is connected across the 16 Ω resistance. The power dissipated in 30 Ω resistance will be maximum when value of R is __________
a) 30 Ω
b) 16 Ω
c) 9 Ω
d) 0
View Answer
Explanation: We know that,
When R = 0, circuit current = \(\frac{V}{30}\) A
And Power dissipated = \(\frac{V^2}{30}\) Watts.
This is the maximum possible value which occurs for R = 0 Ω.
12. Consider a cube having resistance R on each of its sides. For this non-planar graph, the number of independent loop equations are _______________
a) 8
b) 12
c) 7
d) 5
View Answer
Explanation: We know that the number of equations is given by,
L = B – N + 1
Where, B = Number of Branches, N = Number of Nodes
Here, B = 12 and N = 8.
So, L = 12 – 8 + 1 = 5.
13. Given two voltages, 50 ∠0 V and 75 ∠- 60° V. The sum of these voltages is ___________
a) 109 ∠- 60° V
b) 109 ∠- 25° V
c) 109 ∠- 36.6° V
d) 100 ∠- 50.1° V
View Answer
Explanation: The voltages can be written in the form,
50 + j 0.75∠-60°
= 37.5 – j 64.95
So, sum = (50 + 37.5) – j 64.95
= 87.5 – j 64.95 = 109∠-36.6°.
14. For the circuit given below, the value of z21 parameter is ____________
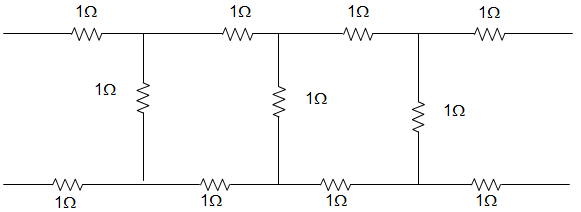
a) z21 = 0.0667 Ω
b) z21 = 2.773 Ω
c) z21 = 1.667 Ω
d) z21 = 0.999 Ω
View Answer
Explanation: z11 = \(\frac{V_1}{I_1}\) = 2 + 1 || [2+1 || (2+1)]
z11 = 2 + 1 || (2 + \(\frac{3}{4}\)) = 2 + \(\frac{1×\frac{11}{4}}{1+\frac{11}{4}} = 2 + \frac{11}{15}\) = 2.733
I0 = \(\frac{1}{1+3}\) I’0 = \(\frac{1}{4}\) I’0
And I’0 = 1 + \(\frac{11}{4}\) I1 = \(\frac{4}{15}\) I1
Or, I0 = \(\frac{1}{4} × \frac{4}{5} I_1 = \frac{1}{15} I_1\)
Or, V2 = I0 = \(\frac{1}{15} I_1\)
z21 = \(\frac{V_2}{I_1} = \frac{1}{15}\) = z12 = 0.0667
z22 = \(\frac{V_2}{I_2}\) = 2+1 || (2+1||3) = z11 = 2.733
∴ [z] = [2.733:0.0667; 0.0667:2.733] Ω.
15. For the circuit given below, the value of z11 parameter is ____________
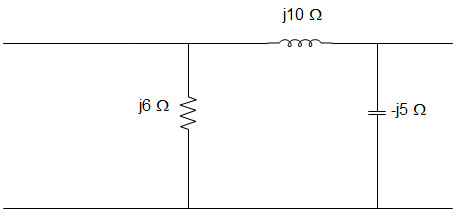
a) z11 = 1.775 + j5.739 Ω
b) z11 = 1.775 – j4.26 Ω
c) z11 = -1.775 – j4.26 Ω
d) z11 = 1.775 + j4.26 Ω
View Answer
Explanation: z1 = \(\frac{12(j10)}{12+j10-j5} = \frac{j120}{12+j5}\)
z2 = \(\frac{j60}{12+j5}\)
z3 = \(\frac{50}{12+j5}\)
z12 = z21 = z2 = \(\frac{(-j60)(12-j5)}{144+25}\) = -1.775 – j4.26
z11 = z1 + z12 = \(\frac{(j120)(12-j5)}{144+25}\) + z12 = 1.775 + j4.26
z22 = z3 + z21 = \(\frac{(50)(12-j5)}{144+25}\) + z21 = 1.7758 – j5.739
∴ [z] = [1.775 + j4.26; -1.775 – j4.26; -1.775 – j4.26; 1.775 – j5.739] Ω.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
