This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Inverse Hybrid (g) Parameter”.
1. For the circuit given below, the value of the Inverse hybrid parameter g11 is ___________
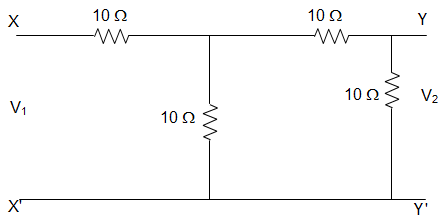
a) 0.067 Ω
b) 0.025 Ω
c) 0.3 Ω
d) 0.25 Ω
View Answer
Explanation: Inverse Hybrid parameter g11 is given by, g11 = \(\frac{I_1}{V_1}\), when I2 = 0.
Therefore short circuiting the terminal Y-Y’, we get,
V1 = I1 ((10||10) + 10)
= I1 \(\left(\left(\frac{10×10}{10+10}\right)+10\right)\)
= 15I1
∴ \(\frac{I_1}{V_1} = \frac{1}{15}\) = 0.067 Ω
Hence g11 = 15 Ω.
2. For the circuit given below, the value of the Inverse hybrid parameter g21 is ___________

a) 0.6 Ω
b) 0.5 Ω
c) 0.3 Ω
d) 0.2 Ω
View Answer
Explanation: Inverse Hybrid parameter g21 is given by, g21 = \(\frac{V_2}{V_1}\), when I2 = 0.
Therefore short circuiting the terminal Y-Y’, and applying Kirchhoff’s law, we get,
V1 = I1 (10 + 10)
V2 = I1 10
∴ \(\frac{V_2}{V_1} = \frac{I_1 10}{I_1 20}\) = 0.5
Hence g21 = 0.5 Ω.
3. For the 2 port network as shown below, the Z-matrix is ___________
![The Z-matrix is [Z1; Z1; Z1; Z1 + Z2] for the 2 port network](https://www.sanfoundry.com/wp-content/uploads/2019/08/network-theory-questions-answers-inverse-hybrid-parameter-q3.png)
a) [Z1; Z1 + Z2; Z1 + Z2; Z3]
b) [Z1; Z1; Z1 + Z2; Z2]
c) [Z1; Z2; Z2; Z1 + Z2]
d) [Z1; Z1; Z1; Z1 + Z2]
View Answer
Explanation: z11 = \(\frac{V_1}{I_1}\), when I2 = 0
z22 = \(\frac{V_2}{I_2}\), when I1 = 0
z12 = \(\frac{V_1}{I_2}\), when I1 = 0
z21 = \(\frac{V_2}{I_1}\), when I2 = 0
Now, in the given circuit putting I1 = 0, we get,
z12 = Z1 and z22 = Z1 + Z2
And putting I2 = 0, we get,
z21 = Z1 and z11 = Z1.
4. Which one of the following parameters does not exist for the two-port network in the circuit given below?
a) h
b) Y
c) Z
d) g
View Answer
Explanation: Y-parameter = \(\frac{1}{Z}\)[1; -1; -1; 1]
And from the definition of the Y parameters, ∆Y = 0. Therefore the Y-parameter exists.
Since ∆Y = 0, so by property of reciprocity, ∆h = 0 and ∆g = 0.
Hence both hybrid and inverse hybrid parameters exist.
But the Z-parameters cannot exist here because if one terminal is opened the circuit will become invalid.
∴ Z- parameters do not exists.
5. In the circuit given below, the value of the Inverse hybrid parameter g11 is _________
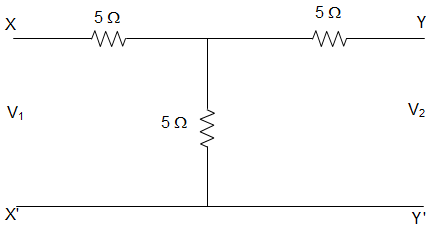
a) 10 Ω
b) 0.133 Ω
c) 5 Ω
d) 2.5 Ω
View Answer
Explanation: Inverse Hybrid parameter g11 is given by, g11 = \(\frac{I_1}{V_1}\), when I2 = 0.
Therefore short circuiting the terminal Y-Y’, we get,
V1 = I1 ((5 || 5) + 5)
= I1 \(\left(\left(\frac{5×5}{5+5}\right)+5\right)\)
= 7.5I1
∴ \(\frac{I_1}{V_1} = \frac{1}{7.5}\) = 0.133
Hence g11 = 7.5 Ω.
6. In the circuit given below, the value of the Inverse hybrid parameter g21 is _________

a) 10 Ω
b) 0.5 Ω
c) 5 Ω
d) 2.5 Ω
View Answer
Explanation: Inverse Hybrid parameter g21 is given by, g21 = \(\frac{V_2}{V_1}\), when I2 = 0.
Therefore short circuiting the terminal Y-Y’, and applying Kirchhoff’s law, we get,
V1 = I1 (5 + 5)
V2 = I1 5
∴ \(\frac{V_2}{V_1} = \frac{I_1 5}{I_1 10}\) = 0.5
Hence g21 = 0.5 Ω.
7. The short-circuit admittance matrix of a two port network is as follows.
[0; -0.5; 0.5; 0]
Then the 2 port network is ____________
a) Non-reciprocal and passive
b) Non-reciprocal and active
c) Reciprocal and passive
d) Reciprocal and active
View Answer
Explanation: The network is non reciprocal because Y12 ≠ Y21 and Y12 is also negative which means either energy storing or providing device is available. So network is active. Therefore the network is Non- reciprocal and active.
8. If a two port network is passive, then we have, with the usual notation, the relationship as _________
a) h21 = h12
b) h12 = -h21
c) h11 = h22
d) h11 h22 – h12 h22 = 1
View Answer
Explanation: We know that, I1 = y11 V1 + y12 V2 ……… (1)
I2 = y21 V1 + y22 V2 ………. (2)
And, V1 = h11 I1 + h12 V2 ………. (3)
I2 = h21 I1 + h22 V2 ……….. (4)
Now, (3) and (4) can be rewritten as,
I1 = \(\frac{V_1}{h_{11}} – \frac{h_{12} V_2}{h_{11}}\) ………. (5)
And I2 = \(\frac{h_{21} V_1}{h_{11}} + \left(- \frac{h_{21} h_{12}}{h_{11}} + h_{22}\right) V_2\) ………. (6)
Therefore using the above 6 equations in representing the hybrid parameters in terms of the Y parameters and applying ∆Y=0, we get,
h11 h22 – h12 h22 = 1 [hence proved].
9. For the circuit given below, the value of the Inverse hybrid parameter g22 is ___________

a) 7.5 Ω
b) 5 Ω
c) 6.25 Ω
d) 3 Ω
View Answer
Explanation: Inverse Hybrid parameter g22 is given by, g22 = \(\frac{V_2}{I_2}\), when V1 = 0.
Therefore short circuiting the terminal X-X’ we get,
-5 I2 – 5 I1 + V2 = 0
-5 I1 – 5(I1 – I2) = 0
Or, 2I1 = I2
Putting the above equation in the first equation, we get,
-7.5 I2 = -V2
Or, \(\frac{V_2}{I_2}\) = 7.5
Hence g22 = 7.5 Ω.
10. In two-port networks the parameter g11 is called _________
a) Short circuit input impedance
b) Short circuit current ratio
c) Open circuit voltage ratio
d) Open circuit input admittance
View Answer
Explanation: We know that, g11 = \(\frac{I_1}{V_1}\), when I2 = 0.
Since the second voltage terminal is short circuited when the ratio of the current and voltage is measured, therefore the parameter g11 is called as Open circuit input admittance.
11. In two-port networks the parameter g21 is called _________
a) Short circuit input impedance
b) Short circuit current ratio
c) Open circuit voltage ratio
d) Open circuit input admittance
View Answer
Explanation: We know that, g21 = \(\frac{V_2}{V_1}\), when I2 = 0.
Since the second output terminal is short circuited when the ratio of the two voltages is measured, therefore the parameter g21 is called as Open circuit voltage ratio.
12. In two-port networks the parameter g12 is called _________
a) Short circuit input impedance
b) Short circuit current gain
c) Open circuit reverse voltage gain
d) Open circuit output admittance
View Answer
Explanation: We know that, g12 = \(\frac{I_1}{I_2}\), when V1 = 0.
Since the primary terminal is short circuited and the ratio of the two currents is measured, therefore the parameter g12 is called as Short circuit current ratio.
13. In two-port networks the parameter g22 is called _________
a) Short circuit input impedance
b) Short circuit current ratio
c) Open circuit voltage ratio
d) Open circuit input admittance
View Answer
Explanation: We know that, g22 = \(\frac{V_2}{I_2}\), when V1 = 0.
Since the primary voltage terminal is short circuited and the ratio of the voltage and current in second loop is measured, therefore the parameter g22 is called as Short circuit current ratio.
14. For a T-network if the Short circuit admittance parameters are given as y11, y21, y12, y22, then y12 in terms of Inverse Hybrid parameters can be expressed as ________
a) y12 = \(\left(g_{11} – \frac{g_{12} g_{21}}{g_{22}}\right)\)
b) y12 = \(\frac{g_{12}}{g_{22}} \)
c) y12 = –\(\frac{g_{21}}{g_{22}} \)
d) y12 = \(\frac{1}{g_{22}}\)
View Answer
Explanation: We know that, I1 = y11 V1 + y12 V2 ……… (1)
I2 = y21 V1 + y22 V2 ………. (2)
And, I1 = g11 V1 + g12 I2 ………. (3)
V2 = g21 V1 + g22 I2 ……….. (4)
Now, (3) and (4) can be rewritten as,
I1 = \(\left(g_{11} – \frac{g_{12} g_{21}}{g_{22}}\right)V_1 + \frac{g_{12}}{g_{22}} V_2\)………. (5)
And I2 = –\(\frac{g_{21} V_1}{g_{22}} + \frac{V_2}{g_{22}}\)………. (6)
∴ Comparing (1), (2) and (5), (6), we get,
y11 = \(\left(g_{11} – \frac{g_{12} g_{21}}{g_{22}}\right)\)
y12 = \(\frac{g_{12}}{g_{22}} \)
y21 = –\(\frac{g_{21}}{g_{22}} \)
y22 = \(\frac{1}{g_{22}}\).
15. For a T-network if the Short circuit admittance parameters are given as y11, y21, y12, y22, then y21 in terms of Inverse Hybrid parameters can be expressed as ________
a) y21 = \(\left(g_{11} – \frac{g_{12} g_{21}}{g_{22}}\right)\)
b) y21 = \(\frac{g_{12}}{g_{22}} \)
c) y21 = –\(\frac{g_{21}}{g_{22}} \)
d) y21 = \(\frac{1}{g_{22}}\)
View Answer
Explanation: We know that, I1 = y11 V1 + y12 V2 ……… (1)
I2 = y21 V1 + y22 V2 ………. (2)
And, I1 = g11 V1 + g12 I2 ………. (3)
V2 = g21 V1 + g22 I2 ……….. (4)
Now, (3) and (4) can be rewritten as,
I1 = \(\left(g_{11} – \frac{g_{12} g_{21}}{g_{22}}\right)V_1 + \frac{g_{12}}{g_{22}} V_2\)………. (5)
And I2 = –\(\frac{g_{21} V_1}{g_{22}} + \frac{V_2}{g_{22}}\)………. (6)
∴ Comparing (1), (2) and (5), (6), we get,
y11 = \(\left(g_{11} – \frac{g_{12} g_{21}}{g_{22}}\right)\)
y12 = \(\frac{g_{12}}{g_{22}} \)
y21 = –\(\frac{g_{21}}{g_{22}} \)
y22 = \(\frac{1}{g_{22}}\).
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Electrical Engineering Internship
- Practice Electrical Engineering MCQs
- Check Electrical Engineering Books
- Practice Electronics & Communication Engineering MCQs
- Check Network Theory Books
