This set of Network Theory Interview Questions and Answers for freshers focuses on “Compensation Theorem”.
1. Reciprocity Theorem is applied for _____ networks.
a) Linear
b) Bilateral
c) Linear bilateral
d) Lumped
View Answer
Explanation: Reciprocity Theorem is applied for linear bilateral networks, not for linear or for linear bilateral or for lumped networks.
2. Reciprocity Theorem is used to find the change in _______ when the resistance is changed in the circuit.
a) Voltage
b) Voltage or current
c) Current
d) Power
View Answer
Explanation: Reciprocity Theorem is used to find the change in voltage or current when the resistance is changed in the circuit. If reciprocity theorem is satisfied the ratio of response to excitation is same for the two conditions.
3. Find the current through 3Ω resistor in the circuit shown below.
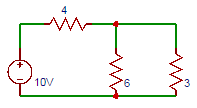
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Total resistance in the circuit = 2+[3||(2+2||2)] = 3.5Ω. The total current drawn by the circuit =10/(4+6||3) = 1.67A. Current through 3Ω resistor = 1.11A ≅1A.
4. Determine the current flowing in the ammeter having 1Ω internal resistance connected in series with the 3Ω resistor as shown in the below circuit.

a) 0.91
b) 0.92
c) 0.93
d) 0.94
View Answer
Explanation: Current through 3Ω resistor = 1.11A. So voltage drop across 1Ω resistor = 1.11×1 = 1.11V. Now the circuit can be modified as
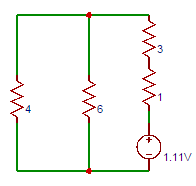
Now current through 3Ω resistor = 0.17A. This current is opposite to the current calculated before. So ammeter reading = (1.11-0.17) = 0.94A.
5. Find the current through 6Ω resistor in the circuit shown below.
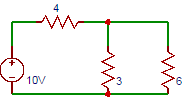
a) 0.33
b) 0.44
c) 0.55
d) 0.66
View Answer
Explanation: Total resistance in the circuit = 4+6||3Ω. The total current drawn by the circuit = 10/(4+6||3)=1.67A. Current through 6Ω resistor = 0.55A.
6. Determine the current flowing in the ammeter having 1Ω internal resistance connected in series with the 6Ω resistor as shown in the below circuit.

a) 0.4
b) 0.45
c) 0.9
d) 0.95
View Answer
Explanation: Current through 3Ω resistor = 0.55A. So voltage drop across 1Ω resistor = 0.55×1 = 0.55V.
Now the circuit can be modified as
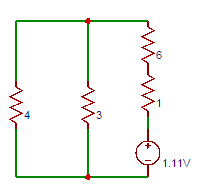
Now current through 6Ω resistor = 0.094A. This current is opposite to the current calculated before. So ammeter reading = (0.55-0.0.94) = 0.45A.
7. Find the current through 6Ω resistor in the circuit shown below.
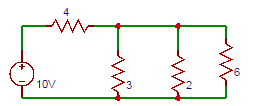
a) 0.11
b) 0.22
c) 0.33
d) 0.44
View Answer
Explanation: Total current in the circuit = 10/(4+3||2||6)=2A. Current through 6Ω resistor = 2×(3||2)/(6+3||2)=0.33A.
8. Consider the following circuit. Determine the current flowing in the ammeter having 1Ω internal resistance in series with the 6Ω resistor.

a) 0.1
b) 0.2
c) 0.3
d) 0.4
View Answer
Explanation:
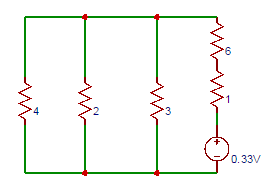
New total current = 0.33/(7+4||2||3)=0.04A. Now reading of ammeter = 0.33-0.04=0.29A ≅ 0.3A.
9. Find the current through 3Ω resistor in the circuit shown below.
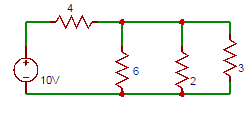
a) 0.45
b) 0.56
c) 0.67
d) 0.78
View Answer
Explanation: Total current = 10 / (4 + (6||2||3) = 2A. Current through 3Ω resistor= 2 x (6||2)/(3 + (6||2)) = 0.67A.
10. Consider the following circuit. Determine the current flowing in the ammeter having 1Ω internal resistance in series with the 3Ω resistor.

a) 0.6
b) 0.7
c) 0.8
d) 0.9
View Answer
Explanation: The current flowing in the ammeter having 1Ω internal resistance in series with the 3Ω resistor shown in the circuit is 0.6 A.
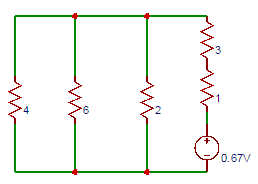
Current through 3Ω resistor = 0.67/(7 + (4||6||2)) = 0.08A. Ammeter reading = 0.67 – 0.08 = 0.59 ≅ 0.6A.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Electrical Engineering Internship
- Practice Electrical Engineering MCQs
- Apply for Electronics & Communication Engineering Internship
- Check Electrical Engineering Books
- Practice Electronics & Communication Engineering MCQs
