This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Dot Convention in Magnetically Coupled Circuits”.
1. A series RLC circuit has a resonance frequency of 1 kHz and a quality factor Q = 100. If each of R, L and C is doubled from its original value, the new Q of the circuit is _____________
a) 25
b) 50
c) 100
d) 200
View Answer
Explanation: Q = \(\frac{f_0}{BW}\)
And f0 = 1/2π (LC)0.5
BW = R/L
Or, Q = \(\frac{1}{R} (\frac{L}{C})^{0.5}\)
When R, L and C are doubled, Q’ = 50.
2. In the circuit given below, the input impedance ZIN of the circuit is _________
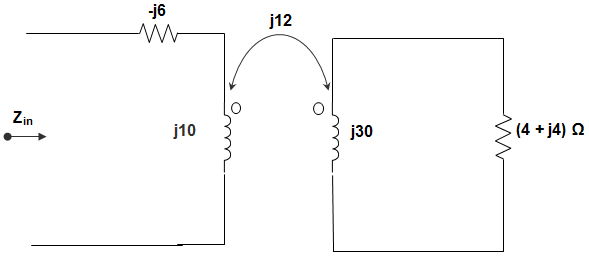
a) 0.52 – j4.30 Ω
b) 0.52 + j15.70 Ω
c) 64.73 + j17.77 Ω
d) 0.3 – j33.66 Ω
View Answer
Explanation: ZIN = (-6j) || (ZA)
ZA = j10 + \(\frac{12^2}{(j30+j6-j2+4)}\)
= 0.49 + j5.82
ZIN = \(\frac{(-j6)(0.49+j5.82)}{(-j6+0.49+j5.82)}\)
= 64.73 + j17.77 Ω.
3. The switch in the circuit shown was on position X for a long time. The switch is then moved to position Y at time t=0. The current I(t) for t>0 is ________
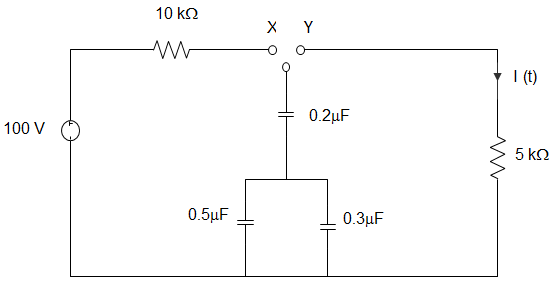
a) 0.2e-125tu(t) mA
b) 20e-1250tu(t) mA
c) 0.2e-1250tu(t) mA
d) 20e-1000tu(t) mA
View Answer
Explanation: CEQ = \(\frac{0.8 × 0.2}{0.8+0.2}\) = 0.16
VC (t=0–) = 100 V
At t≥0,
The discharging current I (t) = \(\frac{V_O}{R} e^{-\frac{t}{RC}}\)
= \(\frac{100}{5000} e^{- \frac{t}{5×10^3×0.16×10^{-6}}}\)
= 0.2e-1250tu(t) mA.
4. In the circuit shown, the voltage source supplies power which is _____________
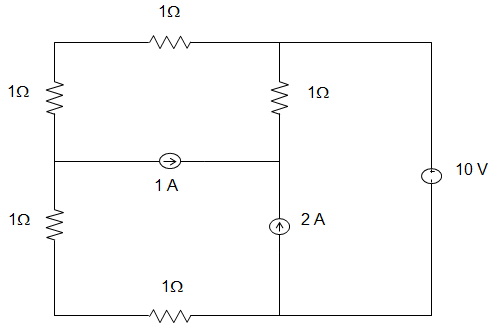
a) Zero
b) 5 W
c) 10 W
d) 100 W
View Answer
Explanation: Let the current supplied by a voltage source.
Applying KVL in outer loop,
10 – (I+3) × (I+1) – (I+2) × 2 = 0
10 – 2(I+3) – 2(I-2) = 0
Or, I = 0
∴ Power VI = 0.
5. In the circuit shown below the current I(t) for t≥0+ (assuming zero initial conditions) is ___________
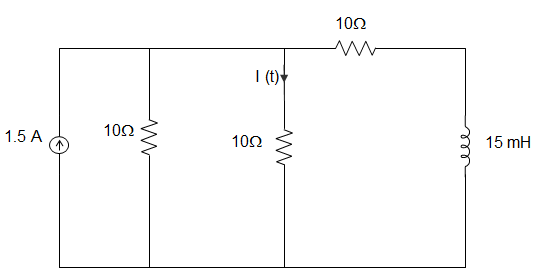
a) 0.5-0.125e-1000t A
b) 1.5-0.125e-1000t A
c) 0.5-0.5e-1000t A
d) 0.375e-1000t A
View Answer
Explanation: I (t) = \(\frac{1.5}{3}\) = 0.5
LEQ = 15 mH
REQ = 5+10 = 15Ω
L = \(\frac{L_{EQ}}{R_{EQ}}\)
= \(\frac{15 × 10^3}{15} = \frac{1}{1000}\)
I (t) A – (A – B) e-t = 0.5 – (0.5-B) e-1000t
= 0.5(0.5 – 0.375) e-1000t
= 0.5 – 0.125 e-1000t
I (t) = 0.5-0.125e-1000t.
6. Initial voltage on capacitor VO as marked |VO| = 5 V, VS = 8 u (t), where u (t) is the unit step. The voltage marked V at t=0+ is _____________
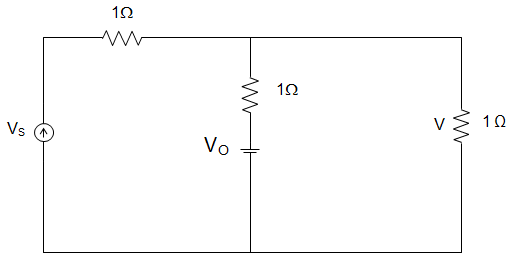
a) 1 V
b) -1 V
c) \(\frac{13}{3}\) V
d) –\(\frac{13}{3}\) V
View Answer
Explanation: Applying voltage divider method, we get,
I = \(\frac{V}{R_{EQ}} \)
= \(\frac{8}{1+1||1} \)
= \(\frac{8}{1+\frac{1}{2}} = \frac{16}{3}\) A
I1 = \(\frac{16}{3} × \frac{1}{2} = \frac{8}{3}\) A
And \(I’_2 = \frac{V}{R_{EQ}} = \frac{5}{1+1||1}\)
= \(\frac{5}{1+\frac{1}{2}} = \frac{10}{3}\) A
Now, \(I’_1 = I’_2 × \frac{1}{1+1} \)
= \(\frac{10}{3} × \frac{1}{2} = \frac{5}{3}\) A
Hence, the net current in 1Ω resistance = I1 + \(I’_1\)
= \(\frac{8}{3} + \frac{5}{3} = \frac{13}{3}\) A
∴ Voltage drop across 1Ω = \(\frac{13}{3} × 1 = \frac{13}{3}\) V.
7. For a unit step signal u (t), the response is V1 (t) = (1-e-3t) for t>0. If a signal 3u (t) + δ(t) is applied, the response will be (considering zero initial conditions)?
a) (3-6e-3t)u(t)
b) (3-3e-3t)u(t)
c) 3u(t)
d) (3+3e-3t)u(t)
View Answer
Explanation: For u (t) = 1, t>0
V1 (t) = (1-e-3t)
Or, V1 (s) = \(\left(\frac{1}{s} + \frac{1}{s+3}\right) = \frac{3}{s(s+3)}\)
And T(s) = \(\frac{V_1 (S)}{u(S)} = \frac{3}{s+3}\)
Now, for R(s) = (\(\frac{3}{s}\) + 1)
Response, H(s) = R(s) T(s) = \((\frac{3+s}{s}) (\frac{3}{s+3}) = \frac{3}{s}\)
Or, h (t) = 3 u (t).
8. In the circuit given below, for time t<0, S1 remained closed and S2 open., S1 is initially opened and S2 is initially closed. If the voltage V2 across the capacitor C2 at t=0 is zero, the voltage across the capacitor combination at t=0+ will be ____________
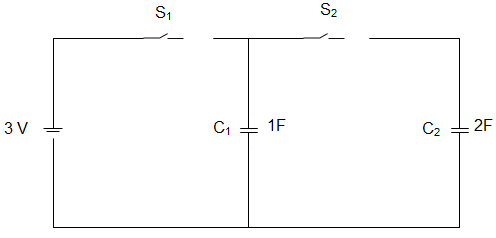
a) 1 V
b) 2 V
c) 1.5 V
d) 3 V
View Answer
Explanation: When S1 is closed and S2 is open,
VC1 (0–) = VC1 (0+) = 3V
When S1 is opened and S2 is closed, VC2 (0+) = VC2 (0+) = 3V.
9. In the circuit given below, the switch S1 is initially closed and S2 is opened. The inductor L carries a current of 10A and the capacitor is charged to 10 V with polarities as shown. The current through C during t=0+ is _____________
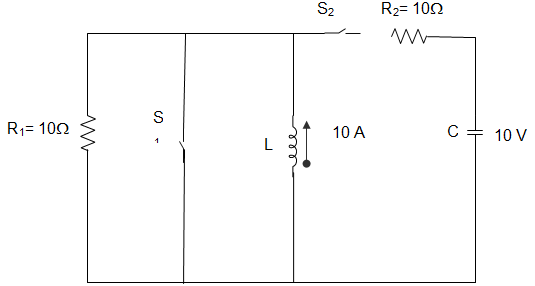
a) 55 A
b) 5.5 A
c) 45 A
d) 4.5 A
View Answer
Explanation: By KCL, we get,
\(\frac{V_L}{10} – 10 + \frac{V_L-10}{10}\) = 0
Hence, 2 VL = 110
∴ VL = 55 V
Or, IC = \(\frac{55-10}{10}\) = 4.5 A.
10. In the circuit given below, the switch S1 is initially closed and S2 is opened. The inductor L carries a current of 10A and the capacitor is charged to 10 V with polarities as shown. The current through L during t=0+ is _____________
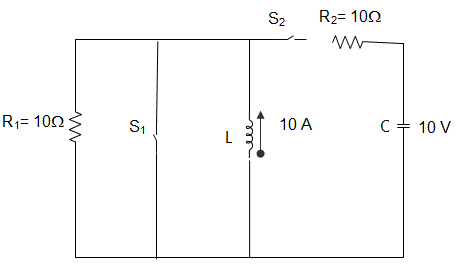
a) 55 A
b) 5.5 A
c) 45 A
d) 4.5 A
View Answer
Explanation: By KCL, we get,
\(\frac{V_L}{10} – 10 + \frac{V_L-10}{10}\) = 0
Hence, 2 VL = 110
∴ VL = 55 V.
11. An ideal capacitor is charged to a voltage VO and connected at t=0 across an ideal inductor L. If ω = \(\frac{1}{\sqrt{LC}}\), the voltage across the capacitor at time t>0 is ____________
a) VO
b) VO cos(ωt)
c) VO sin(ωt)
d) VO e-ωtcos(ωt)
View Answer
Explanation: Voltage across capacitor will discharge through inductor up to voltage across the capacitor becomes zero. Now, inductor will start charging capacitor.
Voltage across capacitor will be decreasing from VO and periodic and is not decaying since both L and C is ideal.
∴ Voltage across the capacitor at time t>0 is VO cos(ωt).
12. In the figure given below, what is the RMS value of the periodic waveform?
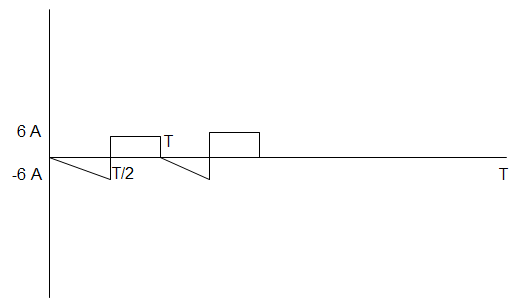
a) 2\(\sqrt{6}\) A
b) 6\(\sqrt{2}\) A
c) \(\sqrt{\frac{4}{3}}\) A
d) 1.5 A
View Answer
Explanation: The rms value for any waveform is = \(\sqrt{\frac{1}{T} \int_0^T f^2 (t)dt)}\)
= \([\frac{1}{T}(\int_0^{\frac{T}{2}}(mt)^2 dt + \int_{\frac{T}{2}}^T 6^2 dt]^{1/2}\)
= \([\frac{1}{T}(\frac{144}{T^2} × \frac{T^3}{3×8} + 36 × \frac{T}{2})]^{\frac{1}{2}}\)
= \([6+18]^{\frac{1}{2}} = \sqrt{24} = 2\sqrt{6}\) A.
13. In the circuit given below, the capacitor initially has a charge of 10 C. The current in the circuit at t=1 sec after the switch S is closed will be ___________
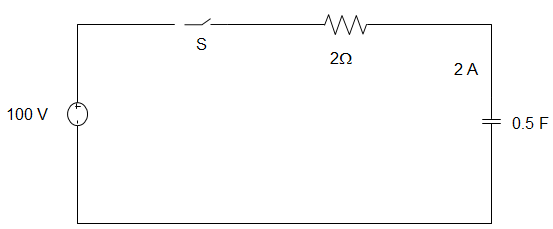
a) 14.7 A
b) 18.5 A
c) 40 A
d) 50 A
View Answer
Explanation: Using KVL, 100 = R\(\frac{dq}{dt} + \frac{q}{C} \)
Or, 100 C = RC\(\frac{dq}{dt}\) + q
Now, \(\int_{q_o}^q \frac{dq}{100C-q} = \frac{1}{RC} ∫_0^t dt\)
Or, 100C – q = (100C – qo) e-t/RC
I = \(\frac{dq}{dt} = \frac{(100C – q_0)}{RC} e^{-1/1}\)
= 40e-1 = 14.7 A.
14. In the circuit given below, the switch is closed at time t=0. The voltage across the inductance just at t=0+ is ____________
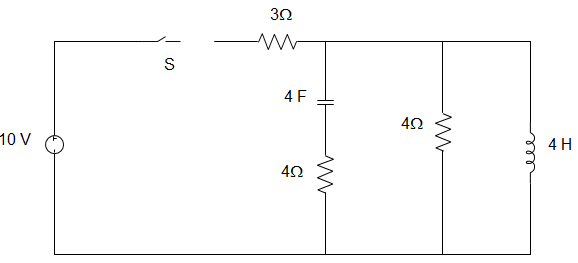
a) 2 V
b) 4 V
c) -6 V
d) 8 V
View Answer
Explanation: A t=0+,
I (0+) = \(\frac{10}{4||4+3} = \frac{10}{5}\) = 2A
∴ I2(0+) = \(\frac{2}{2}\) = 1A
VL(0+) = 1 × 4 = 4 V.
15. A rectangular voltage wave of magnitude A and duration B is applied to a series combination of resistance R and capacitance C. The voltage developed across the capacitor is ____________
a) A[1 – exp(-\(\frac{B}{RC}\))]
b) \(\frac{AB}{RC}\)
c) A
d) A exp(-\(\frac{B}{RC}\))
View Answer
Explanation: VC = \(\frac{1}{C} ∫Idt\)
= \(\frac{1}{C} ∫_0^B \frac{A}{R} e^{-\frac{t}{RC}}\) dt
VC = A[1 – exp(-\(\frac{B}{RC}\))]
Hence, maximum voltage = V [1 – exp (-\(\frac{B}{RC}\))].
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
