This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Nodal Analysis”.
1. If there are N nodes in a circuit, then the number of nodal equations that can be formed are?
a) N+1
b) N
c) N-1
d) N-2
View Answer
Explanation: If there are N nodes in a circuit, then the number of nodal equations that can be formed are N-1. Number of nodal equations = N-1.
2. In the network shown below, find the voltage at node ‘a’.
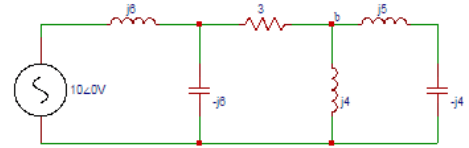
a) 5.22∠104.5⁰
b) 5.22∠-104.5⁰
c) 6.22∠104.5⁰
d) 6.22∠-104.5⁰
View Answer
Explanation: Applying nodal analysis at node ‘a’, (Va-10∠0o)/j6+Va/(-j6)+(Va-Vb)/3=0. Applying nodal analysis at node ‘b’, (Vb-Va)/3+Vb/j4+Vb/j1=0. Solving the above equations we get, Va = 5.22∠-104.5⁰V.
3. Determine the voltage at node ‘b’ in the circuit shown below.

a) -1.34∠-180⁰
b) 1.34∠-180⁰
c) -0.34∠-180⁰
d) 0.34∠-180⁰
View Answer
Explanation: Applying nodal analysis at node ‘a’, (Va-10∠0o)/j6+Va/(-j6)+(Va-Vb)/3=0. Applying nodal analysis at node ‘b’, (Vb-Va)/3+Vb/j4+Vb/j1=0. Solving the above equations we get, Vb = -1.34∠-180⁰V.
4. In the circuit shown below we get a nodal equation as (1/3+1/j4-1/j6)Va—(-1/j6)Vb=x. Find the value of ‘x‘‘.
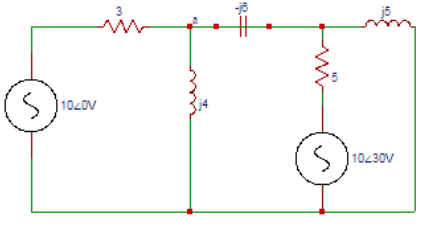
a) (5∠0o)/3
b) – (5∠0o)/3
c) (10∠0o)/3
d) – (10∠0o)/3
View Answer
Explanation: The general equations are YaaVa+YabVb = I1, YbaVa+YbbVb = I2. We get Yaa=1/3+1/j4+1/(-j6) and the self admittance at node a is the sum of admittances connected to node a. Yab=-(1/(-j6)). I1 = (10∠0o)/3=x.
5. Find the value of ‘y’ in the equation –(-1/j6)Va+(1/5+1/j5-1/j6)Vb=y obtained from the following circuit.

a) (10∠30o)/5
b) -(10∠30o)/5
c) (5∠30o)/5
d) (-5∠30o)/5
View Answer
Explanation: We got Ybb=1/5+1/j5-1/j6 and Yab=–(-1/j6). The mutual admittance between node b and a is the sum of the admittances between nodes b and a. I2=-(10∠30o)/5=y.
6. In the circuit shown below find the power dissipated by 2Ω resistor.
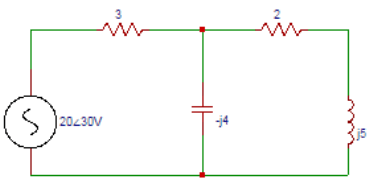
a) 16.24
b) 17.24
c) 18.24
d) 19.24
View Answer
Explanation: Applying nodal analysis at node ‘a’, (Va-20∠30o)/3+Va/(-j4)+Va/(2+j5)=0. On solving, Va = 16.27∠18.91⁰. Current in 2Ω resistor I2 = Va/(2+j5) = (16.27∠18.91o)/(5.38∠68.19o)=3.02∠-49.28o. Power dissipated in 2Ω resistor P=I22 R=3.022×2 = 18.24W.
7. In the circuit shown below. Determine the power dissipated in 3Ω resistor.

a) 7.77
b) 8.77
c) 9.77
d) 10.77
View Answer
Explanation: Current in 3Ω resistor I3 = (-20∠30o+16.27∠18.91o)/3=1.71∠-112o. Power dissipated in 3Ω resistor P=I32 R=1.712×3=8.77W.
8. In the following circuit. Find the power output of the source.

a) 27
b) 28
c) 29
d) 30
View Answer
Explanation: Total power delivered by the source is the product of voltage and current and is given by power output of the source VIcosφ = 20 x 1.71cos142⁰ = 26.95W.
9. For the circuit shown below, find the voltage across the resistance RL if RL is infinite.
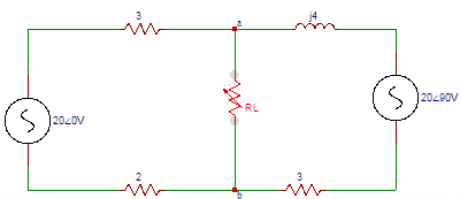
a) 3
b) 2
c) 1
d) 0
View Answer
Explanation: If RL is infinite, the voltage across it will be 0. So the voltage across the resistance RL if RL is infinite is zero.
10. Find the voltage Vab in the circuit shown below.

a) 21.66∠-45.02⁰
b) 20.66∠-45.02⁰
c) 21.66∠45.02⁰
d) 20.66∠45.02⁰
View Answer
Explanation: Applying nodal analysis at node ‘a’, (Va-20∠0o)/(3+2)+(Va-20∠90o)/(j4+3)=0. On solving, we get Va = 21.66∠45.02⁰V.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
