This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Problems Involving Standard Time Functions”.
1. A voltage waveform V (t) = 12t2 is applied across a 1 H inductor for t≥0, with initial current through it being 0. The current through the inductor for t greater than 0 is ___________
a) 12t
b) 24t
c) 12t3
d) 4t3
View Answer
Explanation: We know that, I = \(\frac{1}{L} \int_0^t V \,dt\)
Here, V (t) = 12t2
∴ I = \(\int_0^t 12t^2 \,dt\)
= \(\big[\frac{12t^3}{3}\big]_0^t\) = 4t3 A.
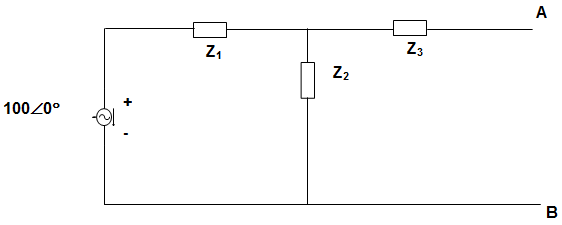
2. In the circuit given below, Z1 = 10∠-60°, Z2 = 10∠60°, Z3 = 50∠53.13°. The Thevenin impedance as seen from A-B is _____________
a) 56.5∠45°
b) 60∠30°
c) 70∠30°
d) 34.4∠65°
View Answer
Explanation: ZTH = ZA-B = Z1 || Z2 + Z3
= \(\frac{Z_1 × Z_2}{Z_1 + Z_2} + Z_3\)
= \(\frac{10∠-60° × 10∠60°}{10∠-60° + 10∠60°}\) + 50∠53.13°
= 56.66∠45°.
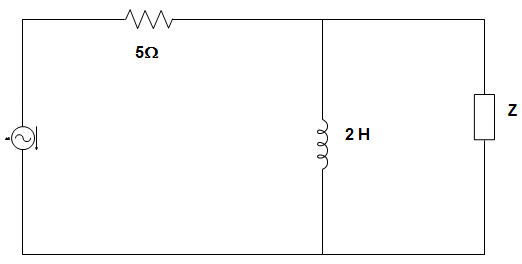
3. In the circuit given below, the value of Z which would cause parallel resonance at 500 Hz is ___________
a) 125 mH
b) 34.20 μF
c) 2 μF
d) 0.05 μF
View Answer
Explanation: At resonance the circuit should have unity power factor
Hence, Z should be capacitive.
Now, \(\frac{1}{jLω} + \frac{1}{1/jCω}\) = 0
Or, \(\frac{-1}{jLω}\) + jCω = 0
∴ C = \(\frac{1}{L × ω^2} = \frac{1}{2 × (2π × 500)^2}\)
= 0.05 μF.
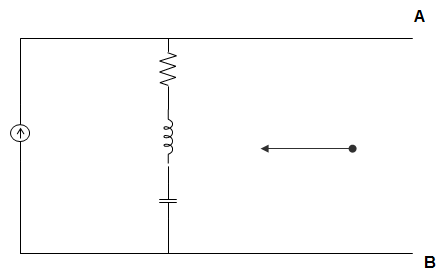
4. In the circuit given below, the current source is 1∠0° A, R = 1 Ω, the impedances are ZC = -j Ω and ZL = 2j Ω. The Thevenin equivalent looking across A-B is __________
a) \(\sqrt{2}\)∠0 V, (1+2j) Ω
b) 2∠45° V, (1-2j) Ω
c) 2∠45° V, (1+j) Ω
d) \(\sqrt{2}\)∠45° V, (1+j) Ω
View Answer
Explanation: ZTH = 1 + (2j-j) = (1 + j) Ω
∴ VTH = 1(1+j) = \(\sqrt{2}\)∠45° V.
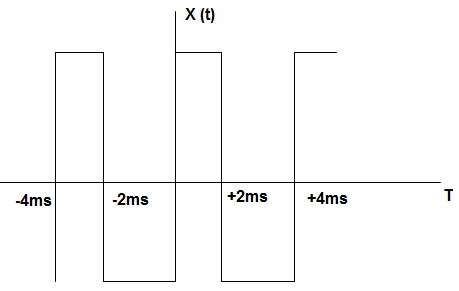
5. A periodic rectangular signal X (t) has the waveform as shown below. The frequency of the fifth harmonic of its spectrum is ______________
a) 40 Hz
b) 200 Hz
c) 250 Hz
d) 1250 Hz
View Answer
Explanation: Periodic time = 4 ms = 4 × 10-3
Fundamental frequency = \(\frac{10^3}{4}\) = 250 Hz
∴ Frequency of the fifth harmonic = 250 × 5 = 1250 Hz.
6. A voltage having the waveform of a sine curve is applied across a capacitor. When the frequency of the voltage is increased, what happens to the current through the capacitor?
a) Increases
b) Decreases
c) Remains same
d) Is zero
View Answer
Explanation: The current through the capacitor is given by,
IC = ωCV cos (ωt + 90°).
As the frequency is increased, IC also increases.
7. An inductive coil connected to a 200 V, 50 Hz AC supply with 10 A current flowing through it dissipates 1000 W. Which of the following will have least value?
a) Resistance R
b) Reactance XL
c) Impedance Z
d) Reactance XC
View Answer
Explanation: Power dissipated is given by,
I2R = 1000 W
Hence, R = \(\frac{1000}{100}\)
Or, R = 10 Ω
Impedance Z = \(\frac{V}{I} = \frac{200}{10}\)
Or, Z = 20 Ω
Reactance XL = \(\sqrt{Z^2 – R^2}\)
= \(\sqrt{20^2 – 10^2}\)
∴ XL = 17.3 Ω.
8. An inductive coil connected to a 200 V, 50 Hz AC supply with 10 A current flowing through it dissipates 1000 W. The value of the impedance Z and Reactance XL are respectively ____________
a) 10 Ω and 15 Ω
b) 20 Ω and 17.3 Ω
c) 17.3 Ω and 20 Ω
d) 15 Ω and 10 Ω
View Answer
Explanation: Power dissipated is given by,
I2R = 1000 W
Hence, R = \(\frac{1000}{100}\)
Or, R = 10 Ω
Impedance Z = \(\frac{V}{I} = \frac{200}{10}\)
Or, Z = 20 Ω
Reactance XL = \(\sqrt{Z^2 – R^2}\)
= \(\sqrt{20^2 – 10^2}\)
∴ XL = 17.3 Ω.
9. A relay coil having voltage of magnitude 210 V and frequency 50 Hz is connected to a 210 V, 50 Hz supply. If it has resistance of 50 Ω and an inductance of 0.2 H, the apparent power is _____________
a) 549.39 VA
b) 275.6 VA
c) 157 VA
d) 187 VA
View Answer
Explanation: Z= 50 + j (0.2) (2π) (50) = 50 + 62.8
S = \(\frac{|V|^2}{Z} = \frac{210^2}{50 – 62.8}\)
Apparent Power |S| = \(\frac{210^2}{\sqrt{50^2 + 62.8^2}}\)
= 549.39 VA.
10. In the circuit given below, the value of ZL for maximum power to be transferred is _____________
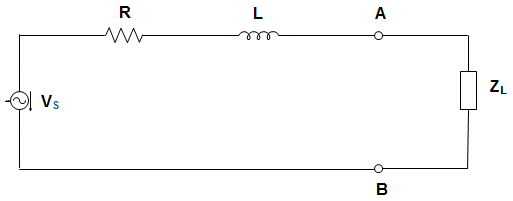
a) R
b) R + jωL
c) R – jωL
d) jωL
View Answer
Explanation: The value of load for maximum power transfer is given by the complex conjugate of ZAB
ZAB = R + jXL
= R + jωL
∴ ZL for maximum power transfer is given by ZL = R – jωL.
11. A 10 V is connected across a load whose V-I characteristics is given by 7I = V2 + 2V. The internal resistance of the battery is of magnitude 1Ω. The current delivered by the battery is ____________
a) 6 A
b) 5 A
c) 7 A
d) 8 A
View Answer
Explanation: 7I = V2 + 2V …………………. (1)
Now, V = 10 – 1 ×I
Putting the value of V in eqt (1), we get,
&I = (10 – I) 2 + 2(10 – I)
Or, I = 100 + I2 – 20I + 20 – 2I
Or, I2 – 29I + 120 = 0…………………. (2)
∴ I = \(\frac{+29 ± \sqrt{29^2 – 4(120)}}{2} = \frac{29 ± 19}{2}\)
I = 5 A, 24 A
Now, I = 24 A is not possible because V will be negative from eqt (2)
∴ I = 5 A.
12. A current I given by I = – 8 + 6\(\sqrt{2}\) (sin (ωt + 30°)) A is passed through three meters. The respective readings (in ampere) will be?
a) 8, 6 and 10
b) 8, 6 and 8
c) – 8, 10 and 10
d) -8, 2 and 2
View Answer
Explanation: PMMC instrument reads only DC value and since it is a centre zero type, so it will give – 8 values.
So, rms = \(\sqrt{8^2 + \left(\frac{6\sqrt{2}}{\sqrt{2}})^2\right)}\) = 10 A
Moving iron also reads rms value, so its reading will also be 10 A.
13. A rectifier type AC voltmeter consists of a series resistance R, an ideal full-wave rectifier bridge and a PMMC instrument. A DC current of 1 mA produces a full-scale deflection of the instrument. The resistance of the instrument is 100 Ω. A voltage of 100 V (rms) is applied to the input terminals. The value of R required is?
a) 63.56 Ω
b) 89.83 Ω
c) 89.83 kΩ
d) 141.3 kΩ
View Answer
Explanation: VOAverage = 0.636 × \(\sqrt{2}\)Vrms = 0.8993 Vrms
The deflection with AC is 0.8993 times that with DC for the same value of voltage V
SAC = 0.8993 SDC
SDC of a rectifier type instrument is \(\frac{1}{I_{fs}}\) where Ifs is the current required to produce full scale deflection, Ifs = 1 mA; Rm = 100 Ω; SDC = 103 Ω/V
SAC = 0.8993 × 1000 = 899.3 Ω/V. Resistance of multiplier RS = SAC V – Rm – 2Rd, where Rd is the resistance of diode, for ideal diode Rd = 0
∴ RS = 899.3 × 100 – 100 = 89.83 kΩ.
14. The discharge of a capacitor through a ballistic galvanometer produces a damped frequency of 0.125 Hz and successive swings of 120, 96 and 76.8 mm. The logarithmic decrement is?
a) 0.225
b) 0.565
c) 0.484
d) 0.7887
View Answer
Explanation: Logarithmic decrement, δ = ln \(\frac{x_1}{x_2} = ln \frac{120}{96}\) = 0.225
Now, δ is related to damping ratio K as, K = \(\frac{1}{\left(1 + (\frac{2π}{δ})^2)^{0.5}\right)}\)
∴ K = 0.0357.
15. 12, 1 H inductors are used as edge to form a cube. The inductance between two diagonally opposite corners of the cube is ____________
a) \(\frac{5}{6}\) H
b) \(\frac{10}{6}\) H
c) 2 H
d) \(\frac{3}{2}\) H
View Answer
Explanation: VAB = \(\frac{1}{3}L + \frac{1}{6} L + \frac{1}{3}L\)
VAB = IL \([\frac{5}{6}] \)
Now, \(\frac{V_{AB}}{I} = \frac{5L}{6}\)
Or, LAB = \(\frac{5L}{6}\)
Here, L = 1Ω
∴ LAB = \(\frac{5}{6}\) H.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Network Theory Books
- Check Electronics & Communication Engineering Books
- Apply for Electrical Engineering Internship
- Practice Electronics & Communication Engineering MCQs
- Practice Electrical Engineering MCQs
