This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Norton’s Theorem Involving Dependent and Independent Sources”.
1. The circuit shown in figure has a load equivalent to _________
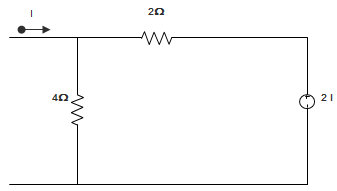
a) \(\frac{4}{3}\) Ω
b) \(\frac{8}{3}\) Ω
c) 4 Ω
d) 2 Ω
View Answer
Explanation: Applying KCL in the given circuit, we get, \(\frac{V}{4} + \frac{V-2I}{2}\) = I
Or, \(\frac{3V-4I}{4}\) = I
Or, 3V = 8I
∴ \(\frac{V}{I} = \frac{8}{3}\) Ω.
2. In the following circuit, the value of Norton’s resistance between terminals a and b are ___________
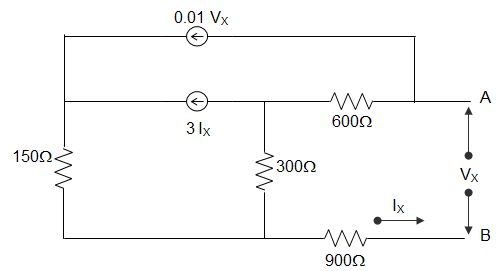
a) RN = 1800 Ω
b) RN = 270 Ω
c) RN = 90 Ω
d) RN = 90 Ω
View Answer
Explanation: By writing loop equations for the circuit, we get,
VS = VX, IS = IX
VS = 600(I1 – I2) + 300(I1 – I2) + 900 I1
= (600+300+900) I1 – 600I2 – 300I3
= 1800I1 – 600I2 – 300I3
I1 = IS, I2 = 0.3 VS
I3 = 3IS + 0.2VS
VS = 1800IS – 600(0.01VS) – 300(3IS + 0.01VS)
= 1800IS – 6VS – 900IS – 3VS
10VS = 900IS
For Voltage, VS = RN IS + VOC
Here VOC = 0
So, Resistance RN = 90Ω.
3. For the circuit shown in figure below, the value of Norton’s resistance is _________
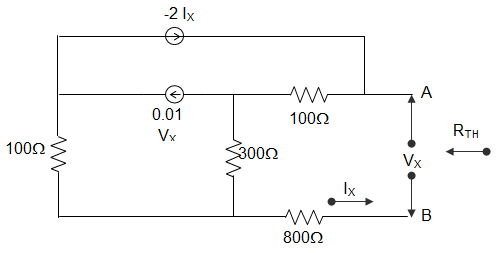
a) 100 Ω
b) 136.4 Ω
c) 200 Ω
d) 272.8 Ω
View Answer
Explanation: IX = 1 A, VX = Vtest
Vtest = 100(1-2IX) + 300(1-2IX – 0.01VS) + 800
Or, Vtest = 1200 – 800IX – 3Vtest
Or, 4Vtest = 1200 – 800 = 400
Or, Vtest = 100V
∴ RN = \(\frac{V_{test}}{1}\) = 100 Ω.
4. For the circuit shown in the figure below, the Norton Resistance looking into X-Y is __________
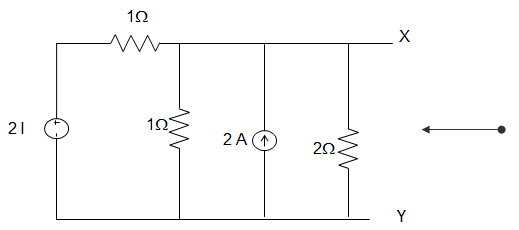
a) 2 Ω
b) \(\frac{2}{3}\)
c) \(\frac{5}{3}\)
d) 2 Ω
View Answer
Explanation: \(R_N = \frac{V_{OC}}{I_{SC}}\)
VN = VOC
Applying KCL at node A, \(\frac{2I-V_N}{1} + 2 = I + \frac{V_N}{2}\)
Or, I = \(\frac{V_N}{1}\)
Putting, 2VN – VN + 2 = VN + \(\frac{V_N}{2}\)
Or, VN = 4 V.
∴ RN = 4/2 = 2Ω.
5. In the figure given below, the value of Resistance R by Norton’s Theorem is ___________
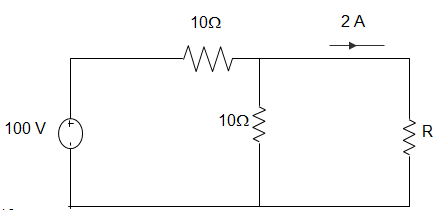
a) 40
b) 20
c) 50
d) 80
View Answer
Explanation: \(\frac{V_P-100}{10} + \frac{V_P}{10}\) + 2 = 0
Or, 2VP – 100 + 20 = 0
∴ VP = 80/2 = 40V
∴ R = 20Ω (By Norton’s Theorem).
6. In the figure given below, the Norton Resistance, as seen at the terminals P-Q, is given by __________
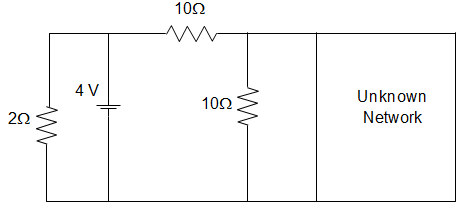
a) 5 Ω
b) 7.5 Ω
c) 5 Ω
d) 7.5 Ω
View Answer
Explanation: For finding VN,
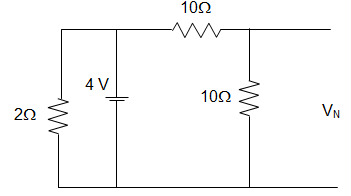
VN = \(\frac{4 × 10}{10+10}\) = 2V
For finding RN,
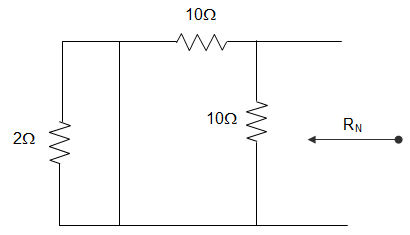
RN = 10 || 10
= \(\frac{10×10}{10+10}\) = 5 Ω.
7. The Norton equivalent impedance Z between the nodes P and Q in the following circuit is __________
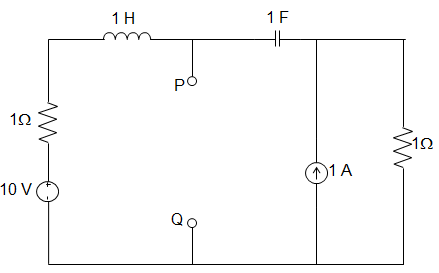
a) 1
b) 1 + s + \(\frac{1}{s}\)
c) 2 + s + \(\frac{1}{s}\)
d) 3 + s + \(\frac{1}{s}\)
View Answer
Explanation: To calculate the Norton resistance, all the current sources get open-circuited and voltage sources get short-circuited.
∴ RN = (\(\frac{1}{s}\) + 1) || (1+s)
= \(\frac{\left(\frac{1}{s} + 1\right)×(1+s)}{\left(\frac{1}{s} + 1\right)+(1+s)}\)
= \(\frac{\frac{1}{s}+1+1+s}{\frac{1}{s}+1+1+s}\) = 1
So, RN = 1.
8. In the circuit given below, it is given that VAB = 4 V for RL = 10 kΩ and VAB = 1 V for RL = 2kΩ. The value of Norton resistance for the network N is ____________
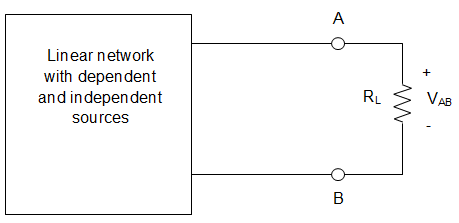
a) 16 kΩ
b) 30 kΩ
c) 3 kΩ
d) 50 kΩ
View Answer
Explanation: When RL = 10 kΩ and VAB = 4 V
Current in the circuit \(\frac{V_{AB}}{R_L} = \frac{4}{10}\) = 0.4 mA
Norton voltage is given by VN = I (RN + RL)
= 0.4(RN + 10)
= 0.4RN + 4
Similarly, for RL = 2 kΩ and VAB = 1 V
So, I = \(\frac{1}{2}\) = 0.5 mA
VN = 0.5(RN + 2)
= 0.5 RN + 1
∴ 0.1RN = 3
Or, RN = 30 kΩ.
9. For the circuit given below, the Norton’s resistance across the terminals A and B is _____________
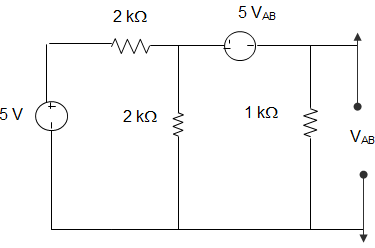
a) 5 Ω
b) 7 kΩ
c) 1.5 kΩ
d) 1.1 kΩ
View Answer
Explanation: Let VAB = 1 V
5 VAB = 5
Or, 1 = 1 × I1 or, I1 = 1
Also, 1 = -5 + 1(I – I1)
∴ I = 7
Hence, R = 7 kΩ.
10. A circuit is given in the figure below. The Norton equivalent as viewed from terminals x and x’ is ___________
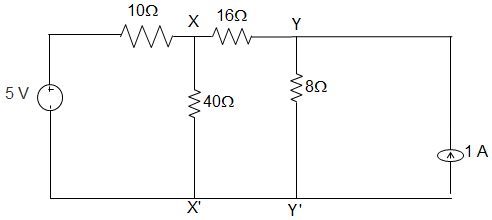
a) 6 Ω and 1.333 A
b) 6 Ω and 0.833 A
c) 32 Ω and 0.156 A
d) 32 Ω and 0.25 A
View Answer
Explanation: We, draw the Norton equivalent of the left side of xx’ and source transformed right side of yy’.
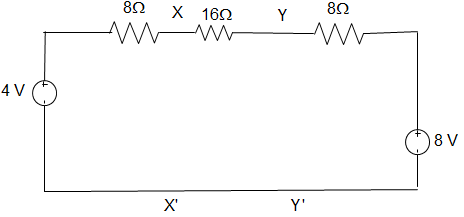
Vxx’ = VN = \(\displaystyle\frac{\frac{4}{8} + \frac{8}{24}}{\frac{1}{8} + \frac{1}{24}}\) = 5V
∴ RN = 8 || (16 + 8)
= \(\frac{8×24}{8+24}\) = 6 Ω
∴ \(I_N = \frac{V_N}{R_N} = \frac{5}{6}\) = 0.833 A.
11. For the circuit given in figure below, the Norton equivalent as viewed from terminals y and y’ is _________
a) 32 Ω and 0.25 A
b) 32 Ω and 0.125 A
c) 6 Ω and 0.833 A
d) 6 Ω and 1.167 A
View Answer
Explanation: We draw the Norton equivalent of the left side of xx’ and source transformed right side of yy’.
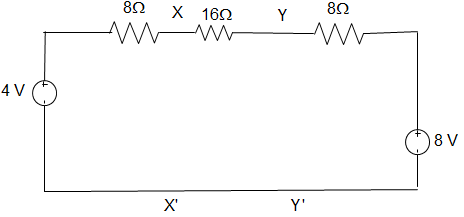
Norton equivalent as seen from terminal yy’ is
Vyy’ = VN =\(\displaystyle\frac{\frac{4}{24} + \frac{8}{8}}{\frac{1}{24} + \frac{1}{8}}\) = 5V
= \(\frac{0.167+1}{0.04167+0.125}\) = 7 V
∴ RN = (8 + 16) || 8
= \(\frac{24×8}{24+8}\) = 6 Ω
∴ IN = \(\frac{V_N}{R_N} = \frac{7}{6}\) = 1.167 A.
12. In the figure given below, the power loss in 1 Ω resistor using Norton’s Theorem is ________
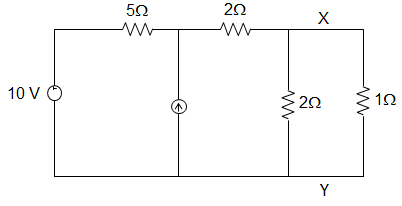
a) 9.76 W
b) 9.26 W
c) 10.76 W
d) 11.70 W
View Answer
Explanation: Let us remove the 1 Ω resistor and short x-y.
At Node 1, assuming node potential to be V, \(\frac{V-10}{5}\) + ISC = 5
But ISC = \(\frac{V}{2}\)
∴ \(\frac{V-10}{5} + \frac{V}{2}\) = 5
Or, 0.7 V = 7
That is, V= 10 V
∴ ISC = \(\frac{V}{2}\) = 5 A
To find Rint, all constant sources are deactivated. Rint = \(\frac{(5+2)×2}{5+2+2} = \frac{14}{9}\) = 1.56 Ω
Rint = 1.56 Ω; ISC = IN = 5A
Here, I = IN \(\frac{R_{int}}{R_{int}+1} = 5 × \frac{1.56}{1.56+1}\) = 3.04 A
∴ Power loss = (3.04)2 × 1 = 9.26 W.
13. The value of RN from the circuit given below is ________
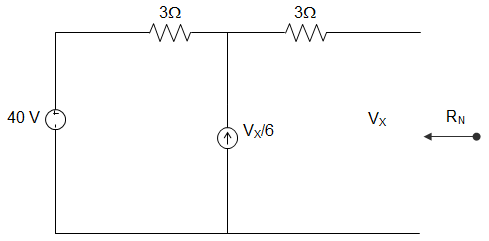
a) 3 Ω
b) 1.2 Ω
c) 5 Ω
d) 12.12 Ω
View Answer
Explanation: VX = 3\(\frac{V_X}{6}\) + 4
Or, VX = 8 V = VOC
If terminal is short-circuited, VX = 0.
ISC = \(\frac{4}{3+3}\) = 0.66 A
∴ RN = \(\frac{V_{OC}}{I_{SC}}\) = \(\frac{8}{0.66}\) = 12.12 Ω.
14. The current I, as shown in the figure below, is ________
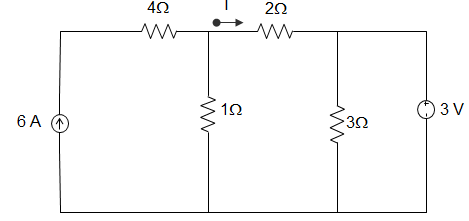
a) 3 A
b) 2 A
c) 1 A
d) 0
View Answer
Explanation: The 3 Ω resistance is an extra element because voltage at node B is independent of the 3 Ω resistance.
I1 = \(\frac{3}{2+1}\) = 1 A (B -> A)
The net current in 2 Ω resistance is I = 1 – I1
= 2 – 1 = 1 A (A -> B).
15. While computing the Norton equivalent resistance and the Norton equivalent current, which of the following steps are undertaken?
a) Both the dependent and independent voltage sources are short-circuited and both the dependent and independent current sources are open-circuited
b) Both the dependent and independent voltage sources are open-circuited and both the dependent and independent current sources are short-circuited
c) The dependent voltage source is open-circuited keeping the independent voltage source untouched and the dependent current source is short-circuited keeping the independent current source untouched
d) The dependent voltage source is short-circuited keeping the independent voltage source untouched and the dependent current source is open-circuited keeping the independent current source untouched
View Answer
Explanation: While computing the Norton equivalent voltage consisting of both dependent and independent sources, we first find the equivalent resistance called the Norton resistance by opening the two terminals. Then while computing the Norton current, we short-circuit the dependent voltage sources keeping the independent voltage sources untouched and open-circuiting the dependent current sources keeping the independent current sources untouched.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Apply for Electronics & Communication Engineering Internship
- Practice Electronics & Communication Engineering MCQs
- Check Network Theory Books
- Practice Electrical Engineering MCQs
- Apply for Electrical Engineering Internship
