Network Theory Questions and Answers – Sinusoidal Response of an R-L-C Circuit

This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Sinusoidal Response of an R-L-C Circuit”.

1. The particular current obtained from the solution of i in the sinusoidal response of R-L-C circuit is?
a) i_p = V/√(R²+(1/ωC+ωL)²) cos⁡(ωt+θ+tan^-1)⁡((1/ωC+ωL)/R))
b) i_p = V/√(R²+(1/ωC-ωL)²) cos⁡(ωt+θ+tan^-1)⁡((1/ωC-ωL)/R))
c) i_p = V/√(R²+(1/ωC+ωL)²) cos⁡(ωt+θ+tan^-1)⁡((1/ωC-ωL)/R))
d) i_p = V/√(R²+(1/ωC-ωL)²) cos⁡(ωt+θ+tan^-1)⁡((1/ωC+ωL)/R))
View Answer

2. In the sinusoidal response of R-L-C circuit, the complementary function of the solution of i is?
a) i_c = c₁ e^(K₁+K₂)t + c₁ e^(K₁-K₂)t
b) i_c = c₁ e^(K₁-K₂)t + c₁ e^(K₁-K₂)t
c) i_c = c₁ e^(K₁+K₂)t + c₁ e^(K₂-K₁)t
d) i_c = c₁ e^(K₁+K₂)t + c₁ e^(K₁+K₂)t
View Answer

3. The complete solution of the current in the sinusoidal response of R-L-C circuit is?
a) i = c₁ e^(K₁+K₂)t + c₁ e^(K₁-K₂)t – V/√(R²+(1/ωC-ωL)²) cos⁡(ωt+θ+tan^-1)⁡((1/ωC-ωL)/R))
b) i = c₁ e^(K₁+K₂)t + c₁ e^(K₁-K₂)t – V/√(R²+(1/ωC-ωL)²) cos⁡(ωt+θ-tan^-1)⁡((1/ωC-ωL)/R))
c) i = c₁ e^(K₁+K₂)t + c₁ e^(K₁-K₂)t + V/√(R²+(1/ωC-ωL)²) cos⁡(ωt+θ+tan^-1)⁡((1/ωC-ωL)/R))
d) i = c₁ e^(K₁+K₂)t + c₁ e^(K₁-K₂)t + V/√(R²+(1/ωC-ωL)²) cos⁡(ωt+θ-tan^-1)⁡((1/ωC-ωL)/R))
View Answer

4. In the circuit shown below, the switch is closed at t = 0. Applied voltage is v (t) = 400cos (500t + π/4). Resistance R = 15Ω, inductance L = 0.2H and capacitance = 3 µF. Find the roots of the characteristic equation.

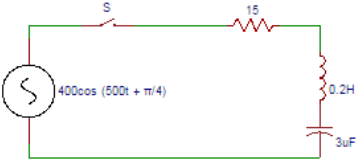
a) -38.5±j1290
b) 38.5±j1290
c) 37.5±j1290
d) -37.5±j1290
View Answer

Answer: d
Explanation: By applying Kirchhoff’s voltage law to the circuit,

On differentiating the above equation and on solving, we get roots of the characteristic equation as -37.5±j1290.

5. In the circuit shown below, the switch is closed at t = 0. Applied voltage is v (t) = 400cos (500t + π/4). Resistance R = 15Ω, inductance L = 0.2H and capacitance = 3 µF. Find the complementary current.

a) i_c = e^-37.5t(c₁cos1290t + c₂sin1290t)
b) i_c = e^-37.5t(c₁cos1290t – c₂sin1290t)
c) i_c = e^37.5t(c₁cos1290t – c₂sin1290t)
d) i_c = e^37.5t(c₁cos1290t + c₂sin1290t)
View Answer

6. In the circuit shown below, the switch is closed at t = 0. Applied voltage is v (t) = 400cos (500t + π/4). Resistance R = 15Ω, inductance L = 0.2H and capacitance = 3 µF. Find the particular solution.

a) i_p = 0.6cos(500t + π/4 + 88.5⁰)
b) i_p = 0.6cos(500t + π/4 + 89.5⁰)
c) i_p = 0.7cos(500t + π/4 + 89.5⁰)
d) i_p = 0.7cos(500t + π/4 + 88.5⁰)
View Answer

7. In the circuit shown below, the switch is closed at t = 0. Applied voltage is v (t) = 400cos (500t + π/4). Resistance R = 15Ω, inductance L = 0.2H and capacitance = 3 µF. Find the complete solution of current.

a) i = e^-37.5t(c₁cos1290t + c₂sin1290t) + 0.7cos(500t + π/4 + 88.5⁰)
b) i = e^-37.5t(c₁cos1290t + c₂sin1290t) + 0.7cos(500t – π/4 + 88.5⁰)
c) i = e^-37.5t(c₁cos1290t + c₂sin1290t) – 0.7cos(500t – π/4 + 88.5⁰)
d) i = e^-37.5t(c₁cos1290t + c₂sin1290t) – 0.7cos(500t + π/4 + 88.5⁰)
View Answer

8. The value of the c₁ in the following equation is?
i = e^-37.5t(c₁cos1290t + c₂sin1290t) + 0.7cos(500t + π/4 + 88.5⁰).
a) -0.5
b) 0.5
c) 0.6
d) -0.6
View Answer

9. The value of the c₂ in the following equation is?
i = e^-37.5t(c₁cos1290t + c₂sin1290t) + 0.7cos(500t + π/4 + 88.5⁰).
a) 2.3
b) -2.3
c) 1.3
d) -1.3
View Answer

10. The complete solution of current obtained by substituting the values of c₁ and c₂ in the following equation is?
i = e^-37.5t(c₁cos1290t + c₂sin1290t) + 0.7cos(500t + π/4 + 88.5⁰).
a) i = e^-37.5t(0.49cos1290t – 1.3sin1290t) + 0.7cos(500t + 133.5⁰)
b) i = e^-37.5t(0.49cos1290t – 1.3sin1290t) – 0.7cos(500t + 133.5⁰)
c) i = e^-37.5t(0.49cos1290t + 1.3sin1290t) – 0.7cos(500t + 133.5⁰)
d) i = e^-37.5t(0.49cos1290t + 1.3sin1290t) + 0.7cos(500t + 133.5⁰)
View Answer

Sanfoundry Global Education & Learning Series – Network Theory.

To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]