This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Attenuators”.
1. The attenuation in dB in terms of input power (P1) and output power (P2) is?
a) log10 (P1/P2)
b) 10 log10 (P1/P2)
c) log10 (P2/P1)
d) 10 log10 (P2/P1)
View Answer
Explanation: The increase or decrease in power due to insertion or substitution of a new element in a network can be conveniently expressed in decibels or in nepers. The attenuation in dB in terms of input power (P1) and output power (P2) is Attenuation in dB = 10 log10 (P1/P2).
2. If V1 is the voltage at port 1 and V2 is the voltage at port 2, then the attenuation in dB is?
a) 20 log10 (V1/V2)
b) 10 log10 (V1/V2)
c) 20 log10 (V2/V1)
d) 10 log10 (V2/V1)
View Answer
Explanation: If V1 is the voltage at port 1 and V2 is the voltage at port 2, then the attenuation in dB is Attenuation in dB = 20 log10 (V1/V2) where V1 is the voltage at port 1 and V2 is the voltage at port 2.
3. What is the attenuation in dB assuming I1 is the input current and I2 is the output current leaving the port?
a) 10 log10 (I1/I2)
b) 10 log10 (I2/I1)
c) 20 log10 (I2/I1)
d) 20 log10 (I1/I2)
View Answer
Explanation: Assuming I1 is the input current and I2 is the output current leaving the port, the attenuation in dB is Attenuation in dB = 20 log10 (I1/I2) where I1 is the input current and I2 is the output current leaving the port.
4. The value of one decibel is equal to?
a) log10 (N)
b) 10 log10 (N)
c) 20 log10 (N)
d) 40 log10 (N)
View Answer
Explanation: The value of one decibel is equal to 20 log10 (N). One decibel = 20 log10 (N) where N is the attenuation.
5. The value of N in dB is?
a) N = anti log(dB)
b) N = anti log(dB/10)
c) N = anti log(dB/20)
d) N = anti log(dB/40)
View Answer
Explanation: The value of N in dB can be expressed as N = anti log(dB/20).
6. In the circuit shown below, find the value of I1/I2.
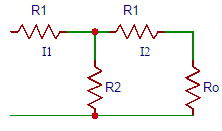
a) (R1-R2+R0)/R2
b) (R1+R2+R0)/R2
c) (R1-R2-R0)/R2
d) (R1+R2-R0)/R2
View Answer
Explanation: R2(I1-I2)=I2(R1+R0)
=> I2(R2+R1+R0)I1R2. On solving, I1/I2=(R1+R2+R1)/R2.
7. Determine the value of N in the circuit shown below.

a) (R1+R2-R0)/R2
b) (R1-R2-R0)/R2
c) (R1+R2+R0)/R2
d) (R1-R2+R0)/R2
View Answer
Explanation: N = I1/I2. We got I1/I2 = (R1+R2+R1)/R2. So on substituting we get N = (R1+R2+R0)/R2.
8. The value of the characteristic impedance R0 in terms of R1 and R2 and R0 in the circuit shown below is?

a) R1+R2(R1+R0)/(R1+R0+R2)
b) R1+ R2(R1+R0)/(R1+R0+R2)
c) R2+ R2(R1+R0)/(R1+R0+R2)
d) R0+R2(R1+R2)/(R1+R0+R2)
View Answer
Explanation: The value of the characteristic impedance R0 in terms of R1 and R2 and R0 when it is terminated in a load of R0 is R0=R1 + R2(R1+R0)/(R1+R0+R2).
9. Determine the value of R1 in terms of R0 and N in the circuit shown below is?

a) R1 = R0(N-1)/(N+1)
b) R1 = R0(N+1)/(N+1)
c) R1 = R0(N-1)/(N-1)
d) R1 = R0(N+1)/(N-1)
View Answer
Explanation: R0 = R1+(R1+R0)/N. On solving, the value of R1 in terms of R0 and N is R1 = R0(N-1)/(N+1).
10. Determine the value of R2 in terms of R0 and N in the circuit shown below is?

a) R2 = NR0/(N2-1)
b) R2 = 2 NR0/(N2-1)
c) R2 = 3 NR0/(N2-1)
d) R2 = 4 NR0/(N2-1)
View Answer
Explanation: NR2 = R1+R0+R2. On substituting the value of R1, we get the value of R2 in terms of R0 and N as R2 = 2 NR0/(N2-1).
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
