This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Advanced Problems on Application of Laplace Transform – 1”.
1. The resistance of a 230 V, 100 W lamp is ____________
a) 529 Ω
b) 2300 Ω
c) 5290 Ω
d) 23 Ω
View Answer
Explanation: P = \(\frac{V^2}{R}\)
Or, R = \(\frac{V^2}{P}\)
Or, R = \(\frac{230 X 230}{100}\)
= 529 Ω.
2. A network has two branches in parallel. One branch contains impedance Za and the other branch has impedance Zb. If it is fed from an AC voltage V of frequency f, the current through Za depends, on which of the following?
a) V, Za, Zb
b) V, Za
c) Za, Zb
d) V, Za, f
View Answer
Explanation: We know that, in parallel branches, the current through any branch depends only on V (voltage), Z (impedance) and f (frequency) only.
So, the current through Za depends on V, Za, and f.
3. Two coils having self-inductances of 1 mH and 2 mH are mutually coupled. The maximum possible mutual inductance is ___________
a) 1.414 mH
b) 2 mH
c) 1 mH
d) 5.5 mH
View Answer
Explanation: We know that, maximum mutual inductance = L1L2
Given that, L1 = 1 mH and L2 = 2 mH
So, maximum mutual inductance = (1 X 2)0.5 = \(\sqrt{2}\)
= 1.414 mH.
4. A constant k band pass filter has a pass band from 100 to 400 Hz. The resonant frequency of series and shunt arms is ____________
a) 300 Hz
b) 250 Hz
c) 200 Hz
d) 150 Hz
View Answer
Explanation: We know that,
Resonant frequency of arms in constant k band pass filter = [(fc1)(fc2)]0.5
Given that, fc1 = 100 Hz and fc2 = 400 Hz
So, Resonant frequency = \(\sqrt{100 X 400}\)
= 200 Hz.
5. An RLC series circuit has Q = 100 and ω0 = 20 rad/sec. The bandwidth is ____________
a) 0.2 rad/sec
b) 2 rad/sec
c) 20 rad/sec
d) 2000 rad/sec
View Answer
Explanation: We know that,
Bandwidth = \(\frac{ω_0}{Q}\)
Given that, ω0 = 20 rad/sec and Q = 100
So, Bandwidth = \(\frac{20}{100}\)
= 0.2 rad/sec.
6. In an unloaded transformer, the flux limiting the primary is 10 mWb and secondary is 30 mWb. The coefficient of coupling is ____________
a) 1
b) 0.1
c) 0.33
d) 0.67
View Answer
Explanation: Φ11 = (1 – k) Φ1
Or, φ11 = φ1 – φ2
Or, φ11 = 30 – 10 = 20 mWb
Now, 20 mWb = (1 – k) 30m
Or, 0.67 = 1 – k
Or, k = 0.33.
7. Poles and zeros of a driving point function of a network are simple and alternate on jω axis. The network consists of ___________
a) R and C
b) L and C
c) R and L
d) R, L and C
View Answer
Explanation: In network having only L and C, poles and zeros of driving point function are simple and alternate on jω axis.
So, the network consists of L and C.
8. In a two terminals network the open circuit voltage measured at the given terminals is 110 V and short circuit currents at the same terminals 10 A. If a load of 50 Ω resistance is connected at the terminals, load current is ___________
a) 1.8 A
b) 1.25 A
c) 6 A
d) 6.25 A
View Answer
Explanation: RTH = \(\frac{110}{10}\) = 11 Ω
So, I = \(\frac{110}{50+11}\) = 1.8 A.
9. A coil has resistance R and inductance L. At ω = ∞ the phase angle between voltage and current is _____________
a) 0°
b) 180°
c) 45°
d) 90°
View Answer
Explanation: We know that,
When ω = ∞, XL = ωL = ∞.
Therefore, θ = tan-1 \(\frac{ωL}{R}\) = 90°.
10. An RLC series circuit has R = 7.07 Ω, L = .707 H and C = 7.07 μF. At Half power frequencies the circuit impedance is ___________
a) 7.07 Ω
b) 10 Ω
c) 14.14 Ω
d) 20 Ω
View Answer
Explanation: We know that,
At half power frequency the circuit impedance is 2 times resistance
Given that, resistance = 7.07 Ω
So, circuit impedance = 2 X 7.07
= 14.14 Ω.
11. Two similar coils have self-inductance of 20 mH each. Coefficient of coupling is 0.4. The mutual inductance M is ______________
a) 2.5 mH
b) 8 mH
c) 7 mH
d) 1 mH
View Answer
Explanation: We know that, the mutual inductance M is given by,
M = k\(\sqrt{L_1 L_2}\)
Given that, k = 0.4, L1 = 20 mH and L2 = 20 mH
So, M = 0.4\(\sqrt{20 X 20}\)
= 8 mH.
12. For any given signal, average power in its 8 harmonic components as 50 mW each and fundamental component also has 50 mV power. Then, average power in the periodic signal is _______________
a) 750
b) 400
c) 100
d) 50
View Answer
Explanation: We know that according to Parseval’s relation, average power is equal to the sum of the average powers in all of its harmonic components.
∴ Pavg = 50×8 = 400.
13. The Current Transformer supplies current to the current coil of a power factor meter, energy meter and, an ammeter. These are connected as?
a) All coils in parallel
b) All coils in series
c) Series-parallel connection with two in each arm
d) Series-parallel connection with one in each arm
View Answer
Explanation: Since the CT supplies the current to the current coil, therefore the coils are connected in series so that the current remains the same. If they were connected in parallel then the voltages would have been same but the currents would not be same and thus efficiency would decrease.
14. A CRO probe has an impedance of 500 kΩ in parallel with a capacitance of 10 pF. The probe is used to measure the voltage between P and Q as shown in the figure. The measured voltage will be?
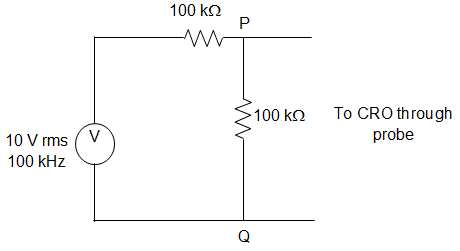
a) 3.53 V
b) 3.47 V
c) 5.54 V
d) 7.00 V
View Answer
Explanation: XC = \(\frac{1}{jCω} = \frac{-j}{2 × 3.14 × 100 × 10^3 × 10 × 10^{-12}}\)
Applying KCL at node,
\(\frac{V_a-10}{100} + \frac{V_a}{100} + \frac{V_a}{500} + \frac{V_a}{-j159}\)
∴ Va = 4.37∠-15.95°.
15. M(t) = 2, 0≤t<4;
t2, t≥4;
The Laplace transform of W (t) is ___________
a) \(\frac{2}{s} – e^{-4s} \left(\frac{2}{s^3} – \frac{8}{s^2} – \frac{14}{s}\right)\)
b) \(\frac{2}{s} + e^{-4s} \left(\frac{2}{s^3} – \frac{8}{s^2} – \frac{14}{s}\right)\)
c) \(\frac{2}{s} – e^{-4s} \left(\frac{2}{s^3} + \frac{8}{s^2} + \frac{14}{s}\right)\)
d) \(\frac{2}{s} + e^{-4s} \left(\frac{2}{s^3} + \frac{8}{s^2} + \frac{14}{s}\right)\)
View Answer
Explanation: M (t) = 2 + u (t) (t2 – 2)
L {2 + u (t) (t2 – 2)} = \(\frac{2}{s}\) + L {u (t) (t2 – 2)}
= \(\frac{2}{s} + e^{-4s}\) L {(t+4)2 -2}
= \(\frac{2}{s} + e^{-4s}\) L {t2 + 8t + 14}
= \(\frac{2}{s} + e^{-4s} \left(\frac{2}{s^3} + \frac{8}{s^2} + \frac{14}{s}\right)\).
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
