This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Transfer Function”.
1. The transfer function of a system having the input as X(s) and output as Y(s) is?
a) Y(s)/X(s)
b) Y(s) * X(s)
c) Y(s) + X(s)
d) Y(s) – X(s)
View Answer
Explanation: The transfer function is defined as the s-domain ratio of the laplace transfrom of the output to the laplace transfrom of the input. The transfer function of a system having the input as X(s) and output as Y(s) is H(s) = Y(s)/X(s).
2. In the circuit shown below, if current is defined as the response signal of the circuit, then determine the transfer function.
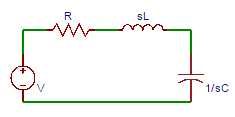
a) H(s)=C/(S2 LC+RCS+1)
b) H(s)=SC/(S2 LC-RCS+1)
c) H(s)=SC/(S2 LC+RCS+1)
d) H(s)=SC/(S2 LC+RCS-1)
View Answer
Explanation: If the current is defined as the response signal of the circuit, then the transfer function H (s) = I/V = 1/(R+sL+1/sC) = sC/(s2Lc+RCs+1) where I corresponds to the output Y(s) and V corresponds to the input X(s).
3. In the circuit shown below, if voltage across the capacitor is defined as the output signal of the circuit, then the transfer function is?
a) H(s)=1/(S2 LC-RCS+1)
b) H(s)=1/(S2 LC+RCS+1)
c) H(s)=1/(S2 LC+RCS-1)
d) H(s)=1/(S2 LC-RCS-1)
View Answer
Explanation: If the voltage across the capacitor is defined as the output signal of the circuit, the transfer function is H(s) = Vo/V = (1/sC)/(R+sL+1/sC)=1/(S2LC+RCS+1).
4. Let us assume x (t) = A cos(ωt + φ), then the Laplace transform of x (t) is?
a) X(S)=A(Scos Ø-ω sinØ)/(S2-ω2)
b) X(S)=A(Scos Ø+ω sinØ)/(S2+ω2)
c) X(S)=A(Scos Ø+ω sinØ)/(S2-ω2)
d) X(S)=A(Scos Ø-ω sinØ)/(S2+ω2)
View Answer
Explanation: We use the transfer function to relate the study state response to the excitation source. And we had assumed that x (t) = A cos(ωt + φ). On expanding and taking the laplace transform we get X(s) = AcosØs/(s2+ω2)-AsinØs/(s2+ω2) = A(Scos Ø-ω sinØ)/(S2+ω2).
5. Let us assume x (t) = A cos(ωt + φ), what is the s-domain expression?
a) Y(s)=H(s) A(Scos Ø-ω sinØ)/(S2-ω2)
b) Y(s)=H(s) A(Scos Ø+ω sinØ)/(S2+ω2)
c) Y(s)=H(s) A(Scos Ø-ω sinØ)/(S2+ω2)
d) Y(s)=H(s) A(Scos Ø+ω sinØ)/(S2-ω2)
View Answer
Explanation: We had the equation Y(s) = H(s)X(s) to find the steady state solution of y(t). The s-domain expression for the response for the input is Y(s)=H(s) A(Scos Ø-ω sinØ)/(S2+ω2).
6. Let us assume x (t) = A cos(ωt + φ), on taking the partial fractions for the response we get?
a) Y(s)=k1/(s-jω)+(k1‘)/(s+jω)+Σterms generated by the poles of H(s)
b) Y(s)=k1/(s+jω)+(k1‘)/(s+jω)+Σterms generated by the poles of H(s)
c) Y(s)=k1/(s+jω)+(k1‘)/(s-jω)+Σterms generated by the poles of H(s)
d) Y(s)=k1/(s-jω)+(k1‘)/(s-jω)+Σterms generated by the poles of H(s)
View Answer
Explanation: By taking partial fractions, Y(s)=k1/(s-jω)+(k1‘)/(s+jω)+Σterms generated by the poles of H(s). The first two terms result from the complex conjugate poles of the deriving source.
7. Let us assume x (t) = A cos(ωt + φ), what is the value of k1?
a) 1/2 H(jω)AejØ
b) H(jω)Ae-jØ
c) H(jω)AejØ
d) 1/2 H(jω)Ae-jØ
View Answer
Explanation: The first two terms on the right hand side of Y(s) determine the steady state response. k1=H(s) (A(scosØ-ωsinØ))/(s+jω)|s=jω = 1/2 H(jω)Ae-jØ.
8. The relation between H (jω) and θ (ω) is?
a) H(jω)=e-jθ (ω)
b) H(jω)=|H(jω)|e-jθ (ω)
c) H(jω)=|H(jω)|ejθ (ω)
d) H(jω)=ejθ (ω)
View Answer
Explanation: In general, H(jω) is a complex quantity, thus H(jω) = |H(jω)|ejθ(ω) where |H(jω)| is the magnitude and the phase angle is θ(ω) of the transfer function vary with frequency ω.
9. Let us assume x (t) = A cos(ωt + φ), what is the value of k1 by considering θ (ω) is?
a) |H(jω)|ej[θ (ω)+Ø]
b) A/2|H(jω)|ej[θ (ω)+Ø]
c) |H(jω)|e-j[θ (ω)+Ø]
d) A/2 |H(jω)|e-j[θ (ω)+Ø]
View Answer
Explanation: The expression of k1 becomes K1 = A/2|H(jω)|ej[θ (ω)+Ø]. We obtain the steady state solution for y(t) by taking the inverse transform ignoring the terms generated by the poles of H(s).
10. Let us assume x (t) = A cos(ωt + φ), What is the final steady state solution for y (t)?
a) A|H(jω)|cos[ωt+Ø+ θ (ω)]
b) A|H(jω)|cos[ωt-Ø+ θ (ω)]
c) A|H(jω)|cos[ωt-Ø- θ (ω)]
d) A|H(jω)|cos[ωt+Ø- θ (ω)]
View Answer
Explanation: We obtain the steady state solution for y (t) by taking the inverse transform of Y(s) ignoring the terms generated by the poles of H (s). Thus yss(t) = A|H(jω)|cos[ωt+Ø+ θ (ω)] which indicates how to use the transfer function to find the steady state response of a circuit.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Electrical Engineering Internship
- Practice Electrical Engineering MCQs
- Check Electrical Engineering Books
- Apply for Electronics & Communication Engineering Internship
- Check Network Theory Books
