This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Millman’s Theorem”.
1. According to Millman’s Theorem, if there are n voltage sources with n internal resistances respectively, are in parallel, then these sources are replaced by?
a) single current source I’ in series with R’
b) single voltage source V’ in series with R’
c) single current source I’ in parallel to R’
d) single voltage source V’ in parallel to R’
View Answer
Explanation: Millman’s Theorem states that if there are voltage sources V1, V2,…… Vn with internal resistances R1, R2,…..Rn, respectively, are in parallel, then these sources are replaced by single voltage source V’ in series with R’.
2. According to Millman’s Theorem, if there are n voltage sources with n internal resistances respectively, are in parallel, then the value of equivalent voltage source is?
a) V‘=(V1G1+V2G2+⋯.+VnGn)
b) V‘=((V1G1+V2G2+⋯.+VnGn))/((1/G1+1/G2+⋯1/Gn))
c) V‘=((V1G1+V2G2+⋯.+VnGn))/(G1+G2+⋯Gn)
d) V‘=((V1/G1+V2/G2+⋯.+Vn/Gn))/( G1+G2+⋯Gn)
View Answer
Explanation: The value of equivalent voltage source is V‘= ((V1G1+V2G2+⋯.+VnGn))/(G1+G2+⋯Gn).
3. According to Millman’s Theorem, if there are n voltage sources with n internal resistances respectively, are in parallel, then the value of equivalent resistance is?
a) R’=G1+G2+⋯Gn
b) R’=1/G1+1/G2+⋯1/Gn
c) R’=1/((G1+G2+⋯Gn))
d) R’=1/(1/G1+1/G2+⋯1/Gn)
View Answer
Explanation: Let the equivalent resistance is R’. The value of equivalent resistance is R’=1/((G1+G2+⋯Gn)).
4. According to Millman’s Theorem, if there are n current sources with n internal conductances respectively, are in series, then these sources are replaced by?
a) single voltage source V’ in parallel with G’
b) single current source I’ in series with G’
c) single current source I’ in parallel with G’
d) single voltage source V’ in series with G’
View Answer
Explanation: Millman’s Theorem states that if there are current sources I1,I2,…… In with internal conductances G1,G2,…..Gn, respectively, are in series, then these sources are replaced by single current source I’ in parallel with G’.
5. According to Millman’s Theorem, if there are n current sources with n internal conductances respectively, are in series, then the value of equivalent current source is?
a) I‘=((I1R1+I2R2+⋯.+InRn))/(R1+R2+⋯Rn)
b) I’=I1R1+I2R2+⋯.+InRn
c) I’=((I1/R1+I2/R2+⋯.+In/Rn))/(R1+R2+⋯Rn)
d) I’=I1/R1+I2/R2+⋯.+In/Rn
View Answer
Explanation: The value of equivalent current source is I‘=((I1R1+I2R2+⋯.+InRn))/(R1+R2+⋯Rn).
6. According to Millman’s Theorem, if there are n current sources with n internal conductances respectively, are in series, then the value of equivalent conductance is?
a) G’=R1+R2+⋯Rn
b) G’=1/(1/R1+1/R2+⋯1/Rn)
c) G’=1/((R1+R2+⋯Rn))
d) G’=1/R1+1/R2+⋯1/Rn
View Answer
Explanation: Let the equivalent conductance is G’. The value of equivalent conductance is G’=1/((R1+R2+⋯Rn)).
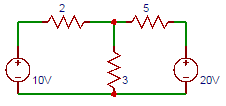
7. Calculate the current through 3Ω resistor in the circuit shown below.
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Applying Nodal analysis the voltage V is given by (10-V)/2+(20-V)/5=V/3. V=8.7V. Now the current through 3Ω resistor in the circuit is I = V/3 = 8.7/3 = 2.9A ≅ 3A.
8. Find the current through 3Ω resistor in the circuit shown below using Millman’s Theorem.

a) 4
b) 3
c) 2
d) 1
View Answer
Explanation: V‘=((V1G1+V2G2))/(G1+G2)=(10(1/2)+20(1/5))/(1/2+1/5)=12.86V. R’=1/((G1+G2))=1/(1/2+1/5)=1.43Ω. Current through 3Ω resistor=I=12.86/(3+1.43)=2.9A≅3A.
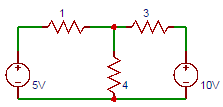
9. Consider the circuit shown below. Find the current through 4Ω resistor.
a) 2
b) 1.5
c) 1
d) 0.5
View Answer
Explanation: Applying Nodal analysis the voltage V is given by (5-V)/1+(10-V)/3=V/4. V=6V. The current through 4Ω resistor I = V/4 = 6/4 = 1.5A.
10. In the following circuit. Find the current through 4Ω resistor using Millman’s Theorem.

a) 0.5
b) 1
c) 1.5
d) 2
View Answer
Explanation: V‘=((V1G1+V2G2))/(G1+G2)=(5(1/1)+10(1/3))/(1/1+1/3)=6.25V. R’=1/((G1+G2))=1/(1/1+1/3)=0.75Ω. I=6.25/(4+0.75)=1.5A.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Electronics & Communication Engineering Internship
- Practice Electrical Engineering MCQs
- Practice Electronics & Communication Engineering MCQs
- Check Electrical Engineering Books
- Check Network Theory Books
