This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Advanced Problems Involving Parameters”.
1. For the circuit given below, the value of Transmission parameter A and C are ____________
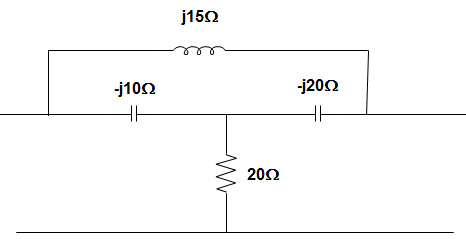
a) A = -0.7692 + j0.3461 Ω, C = 0.03461 + j0.023 Ω
b) A = 0.7692 + j0.3461 Ω, C = 0.03461 + j0.023 Ω
c) A = -0.7692 – j0.3461 Ω, C = -0.03461 + j0.023 Ω
d) A = 0.7692 – j0.3461 Ω, C = 0.023 + j0.03461 Ω
View Answer
Explanation: V = [20 + (-j10) || (j15 − j20)] I1
V1 = \(\Big[20 + \frac{(-j10)(-j5)}{-j15}\Big]\) I1
= [20 – j\(\frac{10}{3}\)] I1
I0 = \(\left(\frac{-j10}{-j10-j5}\right)\) I1 = \(\frac{2}{3}\)I1
V2 = (-j20) I0 + 20I’0
= –\(\frac{j40}{3}I_1 + 20I_1 = (20 – \frac{j40}{3}) I_1 \)
∴ A = \(\frac{V_1}{V_2} = \frac{(20-\frac{j10}{3})I_1}{20-\frac{j40}{3}) I_1}\) = 0.7692 + j0.3461 Ω
∴ C = \(\frac{I_1}{V_2} = \frac{1}{20-j40/3}\) = 0.03461 + j0.023 Ω.
2. For the circuit given below, the value of the Transmission parameter B and D are __________
a) D = 0.5385 + j0.6923 Ω, B = -6.923 + j25.385 Ω
b) D = 0.6923 + j0.5385 Ω, B = 6.923 + j25.385 Ω
c) D = -0.6923 + j0.5385 Ω, B= 25.385 + j6.923 Ω
d) D = -0.5385 + j0.6923 Ω, B = -6.923 + j25.385 Ω
View Answer
Explanation: Z1 = \(\frac{(-j15)(-j10)}{-j15-j10-j20}\) = j10
Z2 = \(\frac{(-j10)(-j20)}{-j15}\) = \(-\frac{j40}{3}\)
Z3 = \(\frac{(j15)(-j20)}{-j15}\) = j20
-I2 = \(\frac{20-j40/3}{20-\frac{j40}{3}+j20}I_1 = \frac{3-j2}{3+j}\) I1
∴ D = \(\frac{-I_1}{I_2} = \frac{3+j}{3-j2}\) = 0.5385 + j0.6923 Ω
V1 = [j10 + 2(9+j7)] I1
= jI1 (24 – j18)
So, B = –\(\frac{V_1}{I_2} = \frac{-jI_1 (24-j18)}{-\frac{3-j2}{3+j} I_1}\)
= \(\frac{6}{13}\)(-15+j55)
∴ B = -6.923 + j25.385 Ω.
3. For the circuit given below, the value of the Transmission parameters A and C are _________________
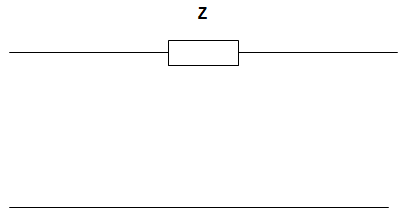
a) A = 0, C = 1
b) A = 1, C = 0
c) A = Z, C = 1
d) A = 1, C = Z
View Answer
Explanation: V1 = V2
Or, A = \(\frac{V_1}{I_2}\) = 1
I1 = 0 or, C = \(\frac{I_1}{V_2}\) = 0.
4. For the circuit given below, the value of the Transmission parameters B and D are _________________
a) B = Z, D = 1
b) B = 1, D = Z
c) B = Z, D = Z
d) B = 1, D = 1
View Answer
Explanation: V1 = ZI1
And I2 = -I1
B = \(\frac{V_1}{I_2}\)
= \(\frac{-ZI_1}{-I_1}\) = Z
D = \(\frac{-I_1}{I_2}\) = 1.
5. For the circuit given below, the value of the Transmission parameters A and C are _______________
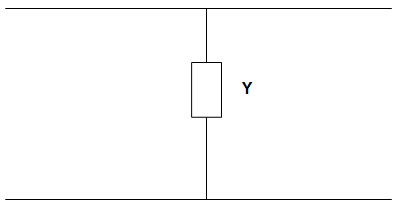
a) A = 1, C = 0
b) A = 0, C = 1
c) A = Y, C = 1
d) A = 1, C = Y
View Answer
Explanation: V1 = V2
∴ A = \(\frac{V_1}{V_2}\) = 1
And V1 = ZI1
∴ C = \(\frac{I_1}{V_2} = \frac{1}{Z}\) = Y.
6. For the circuit given below, the value of the Transmission parameters B and D are ________________
a) B = Y, D = 1
b) B = 1, D = 0
c) B = 0, D = 1
d) B = 0, D = Y
View Answer
Explanation: V1 = V2 = 0
And I2 = -I1
∴ B = \(\frac{V_1}{I_2}\) = 0
∴ D = \(\frac{-I_1}{I_2}\) = 1.
7. For the circuit given below, the values of the h parameter is given as follows h = [16, 3; -2, 0.01]. The value of the ratio \(\frac{V_2}{V_1}\) is ______________
![The value of the ratio I2I1 is -1.6 for values of h parameter is h = [16, 3; -2, 0.01]](https://www.sanfoundry.com/wp-content/uploads/2019/08/network-theory-questions-answers-advanced-problems-involving-parameters-q8.png)
a) 0.3299
b) 0.8942
c) 1.6
d) 0.2941
View Answer
Explanation: Replacing the given 2-port circuit by an equivalent circuit and applying nodal analysis, we get,
V2 = (20) (2I1) = 40 I1
Or, -10 + 20I1 + 3V2 = 0
Or, 10 = 20I1 + (3) (40I1) = 140I1
∴ I1 = \(\frac{1}{14}\) and V2 = \(\frac{40}{14}\)
So, V1 = 16I1 + 3V2 = \(\frac{136}{14}\)
And I2 = (\(\frac{100}{125}\)) (2I1) = \(\frac{-8}{70}\)
∴ \(\frac{V_2}{V_1} = \frac{40}{136}\) = 0.2941.
8. For the circuit given below, the values of the h parameter is given as follows h = [16, 3; -2, 0.01]. The value of the ratio \(\frac{I_2}{I_1}\) is ______________
a) 0.3299
b) 0.8942
c) -1.6
d) 0.2941
View Answer
Explanation: Replacing the given 2-port circuit by an equivalent circuit and applying nodal analysis, we get,
V2 = (20) (2I1) = 40 I1
Or, -10 + 20I1 + 3V2 = 0
Or, 10 = 20I1 + (3) (40I1) = 140I1
∴ I1 = \(\frac{1}{14}\) and V2 = \(\frac{40}{14}\)
So, V1 = 16I1 + 3V2 = \(\frac{136}{14}\)
And I2 = (\(\frac{100}{125}\)) (2I1) = \(\frac{-8}{70}\)
∴ \(\frac{I_2}{I_1}\) = -1.6.
9. If for a circuit the value of the h parameter is given as h = [8, 2/3; -2/3, 4/9]. Then the value of the voltage source V is _________________
a) 2.38 V
b) 1.19 V
c) 1.6 V
d) 3.2 V
View Answer
Explanation: 8I1 + \(\frac{2}{3V_2}\) = 10
V2 = \(\frac{2}{3}\)I1 (5||\(\frac{9}{4}\))
= \(\frac{2}{3}\)I1 \((\frac{45}{29})= \frac{30}{29}I_1\)
I1 = \(\frac{29}{30}\)V2
(8)(\(\frac{29}{30}\)) V2 + \(\frac{2}{3}\)V2 = 10
V2 = \(\frac{300}{252}\) = 1.19 V.
10. For a 2-port network, the value of the h parameter is as h=[600, 0.04; 30, 2×10-3]. Given that, ZS = 2 kΩ and ZL = 400 Ω. The value of the parameter Zin is ______________
a) 250 Ω
b) 333.33 Ω
c) 650 Ω
d) 600 Ω
View Answer
Explanation: Zin = hie – \(\frac{h_{re} h_{fe} R_L}{1 + h_{oe} R_L}\)
= h11 – \(\frac{h_{12} h_{21} R_L}{1+h_{22} R_L}\)
= 600 – \(\frac{0.04×30×400}{1+2×10^{-3}×400}\) = 333.33 Ω.
11. For a 2-port network, the value of the h parameter is as h=[600, 0.04; 30, 2×10-3]. Given that, ZS = 2 kΩ and ZL = 400 Ω. The value of the parameter Zout is ______________
a) 650 Ω
b) 500 Ω
c) 250 Ω
d) 600 Ω
View Answer
Explanation: Zout = \(\frac{R_s+h_{ie}}{(R_s+h_{ie}) h_{oe}-h_{re} h_{fe}}\)
= \(\frac{R_s+h_{11}}{(R_s+h_{11}) h_{22}-h_{21} h_{12}}\)
= \(\frac{2000+600}{2600×2×10^{-3}-30×0.04}\) = 650 Ω.
12. For the circuit given below, the value of the g11 and g21 are _________________
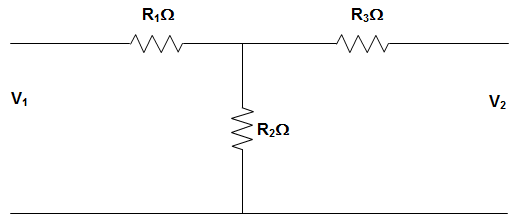
a) g11 = –\(\frac{1}{R_1+R_2}\), g21 = \(\frac{R_2}{R_1+R_2}\)
b) g11 = \(\frac{1}{R_1-R_2}\), g21 = –\(\frac{R_2}{R_1+R_2}\)
c) g11 = \(\frac{1}{R_1+R_2}\), g21 = \(\frac{R_2}{R_1+R_2}\)
d) g11 = \(\frac{1}{R_1-R_2}\), g21 = \(\frac{R_2}{R_1-R_2}\)
View Answer
Explanation: I1 = \(\frac{V_1}{R_1+R_2}\)
Or, g11 = \(\frac{I_1}{V_1} = \frac{1}{R_1+R_2}\)
By voltage division, V2 = \(\frac{R_2}{R_1+R_2}\)V1
Or, g21 = \(\frac{V_2}{V_1} = \frac{R_2}{R_1+R_2}\).
13. For the circuit given below, the value of the g12 and g22 are _______________
a) g12 = –\(\frac{R_2}{R_1+R_2}\), g22 = R3 + \(\frac{R_1 R_2}{R_1+R_2}\)
b) g12 = \(\frac{R_2}{R_1+R_2}\), g22 = -R3 + \(\frac{R_1 R_2}{R_1+R_2}\)
c) g12 = –\(\frac{R_2}{R_1+R_2}\), g22 = R3 – \(\frac{R_1 R_2}{R_1+R_2}\)
d) g12 = \(\frac{R_2}{R_1+R_2}\), g22 = -R3 – \(\frac{R_1 R_2}{R_1+R_2}\)
View Answer
Explanation: I1 = –\(\frac{R_2}{R_1+R_2}\)I2
Or, g12 = \(\frac{I_1}{I_2} = -\frac{R_2}{R_1+R_2}\)
Also, I2 (R3 + R1 //R2)
= I2 \((R_3 + \frac{R_1 R_2}{R_1+R_2})\)
∴ g22 = \(\frac{V_2}{I_2} = R_3 + \frac{R_1 R_2}{R_1+R_2}\).
14. For the circuit given below, the value of g11 and g21 are _________________
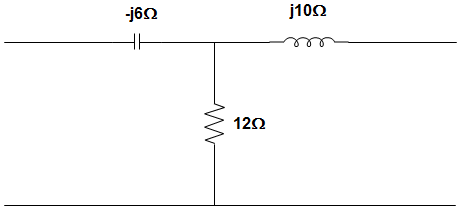
a) g11 = 0.0667 – j0.0333 Ω, g21 = 0.8 + j0.4 Ω
b) g11 = -0.0667 – j0.0333 Ω, g21 = -0.8 – j0.4 Ω
c) g11 = 0.0667 + j0.0333 Ω, g21 = 0.8 + j0.4 Ω
d) g11 = -0.0667 + j0.0333 Ω, g21 = 0.8 – j0.4 Ω
View Answer
Explanation: V1 = (12-j6) I1
Or, g11 = \(\frac{I_1}{V_1} = \frac{1}{12-j6}\) = 0.0667 + j0.0333 Ω
g21 = \(\frac{V_2}{V_1} = \frac{12I_1}{(12-j6) I_1}\)
= \(\frac{2}{2-j}\) = 0.8 + j0.4 Ω.
15. For the circuit given below, the value of g12 and g22 are ________________
a) g12 = 0.8 + j0.4 Ω, g22 = 2.4 + j5.2 Ω
b) g12 = -0.8 + j0.4 Ω, g22 = -2.4 – j5.2 Ω
c) g12 = 0.8 – j0.4 Ω, g22 = 2.4 – j5.2 Ω
d) g12 = -0.8 – j0.4 Ω, g22 = 2.4 + j5.2 Ω
View Answer
Explanation: I1 = \(\frac{-12}{12-j6}\)I2
Or, g12 = \(\frac{I_1}{I_2}\) = -g21 = -0.8 – j0.4 Ω
V2 = (j10 + 12 || -j6) I2
g22 = \(\frac{V_2}{I_2}\) = 2.4 + j5.2 Ω.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
