Final Value Theorem Problems Questions and Answers

This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Problems on Initial and Final Value Theorem”.

1. What is the steady state value of F (t), if it is known that F(s) = \(\frac{2}{s(S+1)(s+2)(s+3)}\)?
a) \(\frac{1}{2}\)
b) \(\frac{1}{3}\)
c) \(\frac{1}{4}\)
d) Cannot be determined
View Answer

Answer: b
Explanation: From the equation of F(s), we can infer that, a simple pole is at origin and all other poles are having negative real part.
∴ F(∞) = lim_s→0 s F(s)
= lim_s→0 \(\frac{2s}{s(S+1)(s+2)(s+3)}\)
= \(\frac{2}{(s+1)(s+2)(s+3)}\)
= \(\frac{2}{6} = \frac{1}{3}\).

2. What is the steady state value of F (t), if it is known that F(s) = \(\frac{1}{(s-1)(s+2)}\)?
a) 1
b) –\(\frac{1}{2}\)
c) \(\frac{1}{2}\)
d) Cannot be determined
View Answer

Answer: d
Explanation: The steady state value of this Laplace transform is cannot be determined since; F(s) has a pole s = 1. Hence the answer is that it cannot be determined.

3. What is the steady state value of F (t), if it is known that F(s) = \(\frac{1}{(s+2)^2 (s+4)}\)?
a) \(\frac{1}{16}\)
b) Cannot be determined
c) 0
d) \(\frac{1}{8}\)
View Answer

Answer: c
Explanation: The steady state value of F(s) exists since all poles of the given Laplace transform have negative real part.
∴F(∞) = lim_s→0 s F(s)
= lim_s→0 \(\frac{s}{(s+2)^2 (s+4)}\)
= 0.

4. What is the steady state value of F (t), if it is known that F(s) = \(\frac{10}{(s+1)(s^2+1)}\)?
a) -5
b) 5
c) 10
d) Cannot be determined
View Answer

Answer: d
Explanation: The steady state value of this Laplace transform is cannot be determined since; F(s) is having two poles on the imaginary axis (j and –j). Hence the answer is that it cannot be determined.

5. What is the steady state value of F (t), if it is known that F(s) = b/(s(s+1)(s+a)), where a>0?
a) \(\frac{b}{a}\)
b) \(\frac{a}{b}\)
c) 1
d) Cannot be determined
View Answer

Answer: a
Explanation: F (∞) = lim_s→0 s F(s)
= lim_s→0 \(\frac{sb}{s(s+1)(s+a)}\)
= lim_s→0 \(\frac{b}{(s+1)(s+a)}\)
= \(\frac{b}{a}\).

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. The inverse Laplace transform of F(s) = \(\frac{2}{s^2+3s+2}\) is ______________
a) -2e^-2t + 2e^-t
b) 2e^-2t + 2e^-t
c) -2e^-2t – 2e^-t
d) 2e^-t + e^-2t
View Answer

Answer: a
Explanation: s² + 3s + 2 = (s+2) (s+1)
Now, F(s) = \(\frac{A}{(s+2)} + \frac{B}{(s+1)}\)
Hence, A = (s+2) F(s) |_s=-2
= \(\frac{2}{s+1}\)|_s=-2 = -2
And, B = (s+1) F(s) |_s=-1
= \(\frac{2}{s+2}\)|_s=-1 = 2
∴ F(s) = \(\frac{-2}{(s+2)} + \frac{2}{(s+1)}\)
∴ F (t) = L^-1{F(s)}
= -2e^-2t + 2e^-t for t≥0.

7. The inverse Laplace transform of F(s) = \(\frac{2}{s+c}e^{-bs}\) is _____________
a) 2e^{-k (t+b)} u (t+b)
b) 2e^{-k (t-b)} u (t-b)
c) 2e^{k (t-b)} u (t-b)
d) 2e^{k (t-b)} u (t+b)
View Answer

Answer: b
Explanation: Let G(s) = \(\frac{2}{s+c}\)
Or, G (t) = L^-1{G(s)} = 2e^-ct
∴ F (t) = L^-1{G(s) e^-bs}
= 2e^{-k (t-b)} u (t-b).

8. The inverse Laplace transform of F(s) = \(\frac{3s+5}{s^2+7}\) is _____________
a) 3 sin (\(\sqrt{7}\)t) – \(\frac{5}{\sqrt{7}}\) cos (\(\sqrt{7}\) t)
b) 3 sin (\(\sqrt{7}\)t) + \(\frac{5}{\sqrt{7}}\) cos (\(\sqrt{7}\) t)
c) 3 cos (\(\sqrt{7}\)t) + \(\frac{5}{\sqrt{7}}\) sin (\(\sqrt{7}\) t)
d) 3 cos (\(\sqrt{7}\)t) – \(\frac{5}{\sqrt{7}}\) sin (\(\sqrt{7}\) t)
View Answer

Answer: c
Explanation: F (t) = L^-1{F(s)}
= L^-1\(\Big\{\frac{3s}{s^2+7} + \frac{5}{s^2+7}\Big\}\)
= L^-1\(\Big\{\frac{3s}{s^2 + \sqrt{7}^2} + \frac{5}{\sqrt{7}} \frac{\sqrt{7}}{s^2 +\sqrt{7}^2}\Big\}\)
The inverse Laplace transform is = 3 cos (\(\sqrt{7}\)t) + \(\frac{5}{\sqrt{7}}\) sin (\(\sqrt{7}\) t).

9. The inverse Laplace transform of F(s) = \(\frac{5}{s^2-9}\) is ______________
a) \(\frac{1}{6}e^{3t} + \frac{5}{6e^{-3t}}\)
b) \(\frac{1}{6}e^{3t} – \frac{5}{6e^{-3t}}\)
c) \(\frac{5}{6}e^{3t} + \frac{5}{6e^{-3t}}\)
d) \(\frac{5}{6}e^{3t} – \frac{5}{6e^{-3t}}\)
View Answer

Answer: d
Explanation: F (t) = L^-1{F(s)}
= L^-1{\(\frac{5}{s^2-9}\)}
= L^-1\({\frac{A}{s-3} + \frac{B}{s+3}}\)
Hence, A = (s-3) \(\frac{5}{(s-3)(s+3)}|_{s=3} = \frac{5}{6}\)
And, B = (s+3) \(\frac{5}{(s-3)(s+3)}|_{s=-3} = -\frac{5}{6}\)
The inverse Laplace transform is \(\frac{5}{6}e^{3t} – \frac{5}{6e^{-3t}}\).

10. The inverse Laplace transform of F(s) = \(\frac{e^{-3s}}{s(s^2+3s+2)}\) is ______________
a) {0.5 + 0.5e^-2(t+3) – e^-(t+3)} u (t+3)
b) {0.5 + 0.5e^-2(t+3) – e^-(t-3)} u (t-3)
c) {0.5 – 0.5e^-2(t-3) – e^-(t-3)} u (t-3)
d) 0.5 + 0.5e^-2t – e^-t)
View Answer

Answer: b
Explanation: Let G(s) = \(\frac{1}{s(s^2+3s+2)}\)
Or, F(s) = G(s) e^-3s
G (t) = L^-1{G(s)}
= L^-1\({\frac{A}{s} + \frac{B}{s+2} + \frac{C}{s+1}}\)
Solving we get, A = 0.5, B = 0.5, C = -1
So, G (t) = 0.5 + 0.5e^-2t-e^-t
The inverse Laplace transform is F (t) = {0.5 + 0.5e^-2(t+3) – e^-(t-3)} u (t-3).

11. Given a sinusoidal voltage that has a peak to peak value of 100 V. The RMS value of the sinusoidal voltage is ___________
a) 50 V
b) 70.7 V
c) 35.35 V
d) 141.41 V
View Answer

Answer: c
Explanation: Given that,
Peak value = 50 V
We know that, RMS value = \(\frac{Peak \,Value}{\sqrt{2}}\)
= \(\frac{50}{\sqrt{2}}\) = 35.35 V.

12. The Laplace transform of F(t) = sin(2t)cos(2t) is ______________
a) \(\frac{4}{2(s^2+16)}\)
b) \(\frac{1}{s+4} – \frac{2}{s+2} + \frac{1}{s}\)
c) \(\frac{2}{s^3}\)
d) \(\frac{1}{2s} + \frac{s}{2(s^2+36)}\)
View Answer

Answer: a
Explanation: Using the Trigonometric Identity,
We get, sin (2t) cos (2t) = \(\frac{1}{2}\) (sin (4t))
∴L {sin (2t) cos (2t)} = \(\frac{4}{2(s^2+16)}\).

13. Convolution of step signal 100 times that is 100 convolution operations. The Laplace transform is ______________
a) \(\frac{1}{s^{100}}\)
b) \(\frac{1}{s^{50}}\)
c) 1
d) s¹⁰⁰
View Answer

Answer: a
Explanation: n times = u (t) * u (t) * …… * u (t)
Laplace transform of the above function = \(\frac{1}{s^n}\), where n is number of convolutions.
∴ Laplace transform for 100 convolutions = \(\frac{1}{s^{100}}\).

14. For the circuit given below, the Time-constant is __________

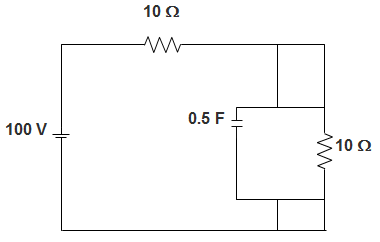
a) 1.5
b) 1.25
c) 2.5
d) 2.25
View Answer

Answer: b
Explanation: We know that,
Time constant is given by R_eq.C
The equivalent resistance is given by,
R_eq = R || R
= \(\frac{R*R}{R+R}\)
= \(\frac{R}{2}\)
= 5 Ω
So, Time-constant = \(\frac{5X0.5}{2}\)
= 1.25.

15. In a dual slop integrating type digital voltmeter, the first integrating is carried out for 50 periods of the supply frequency of 50 Hz. If the reference voltage used is 10 V, the total conversion time for an input of 40 V is?
a) 3 s
b) 2 s
c) 4 s
d) 1 s
View Answer

Answer: c
Explanation: In a dual slope integrating digital voltmeter,
\((\frac{t_1}{t_2})\) V_in = V_ref
Where, t₁ = first integration time = 50 × \(\frac{1}{50}\) = 1
But V_in = 40 V and V_ref = 10 V
∴ t₂ = \(\frac{V_{in} t_1}{V_{ref}}\) = 4 s.

Sanfoundry Global Education & Learning Series – Network Theory.

To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Network Theory Questions and Answers – Laplace Transform of a Periodic Function

» Next - Network Theory Questions and Answers – Calculation of I(0+), di/dt(0+), d2I/dt2(0+) in Circuits Involving both Capacitor and Inductor

Related Posts:

Practice Electronics & Communication Engineering MCQs
Practice Electrical Engineering MCQs
Check Electrical Engineering Books
Apply for Electronics & Communication Engineering Internship
Apply for Electrical Engineering Internship

Recommended Articles: