This set of Network Theory Questions & Answers for Exams focuses on “Advanced Problems on Reciprocity Theorem”.
1. In Reciprocity Theorem, which of the following ratios is considered?
a) Voltage to current
b) Current to current
c) Voltage to voltage
d) No ratio is considered
View Answer
Explanation: The Reciprocity Theorem states that if an Emf E in one branch produces a current I in a second branch, then if the same emf E is moved from the first to the second branch, it will produce the same current in the first branch, when the Emf E in the first branch is replaced with a short circuit. Therefore the ratio of Voltage to Current is considered in case of Reciprocity Theorem.
2. The Reciprocity Theorem is valid for ___________
a) Non-Linear Time Invariant circuits
b) Linear Time Invariant circuits
c) Non-Linear Time Variant circuits
d) Linear Time Variant circuits
View Answer
Explanation: A reciprocal network comprises of linear time-invariant bilateral elements. It is applicable to resistors, capacitors, inductors (including coupled inductors) and transformers. However, both dependent and independent sources ate not permissible.
3. In the circuit given below, the current in the 4-ohm resistor is __________
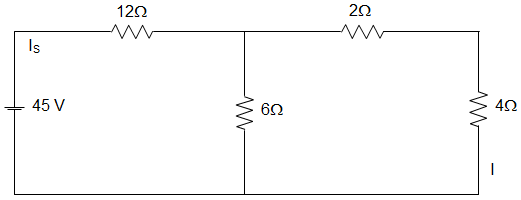
a) 3.5 A
b) 2.5 A
c) 1.5 A
d) 0.5 A
View Answer
Explanation: Rth = [(2+4) || 6] + 12 = 15 Ω
IS = \(\frac{45}{15}\) = 3 A
Now, by current division rule, we get, I = \(\frac{3 × 6}{12} = \frac{18}{12}\) = 1.5 A.
4. The Reciprocity Theorem is applicable for __________
a) Single-source networks
b) Multi-source networks
c) Both Single and Multi-source networks
d) Neither Single nor Multi-source networks
View Answer
Explanation: According to Reciprocity Theorem, the voltage source and the resulting current source may be interchanged without a change in current. Therefore the theorem is applicable only to single-source networks. It therefore cannot be employed in multi-source networks.
5. In the circuit given below, the current through the 12 Ω resistance is _________
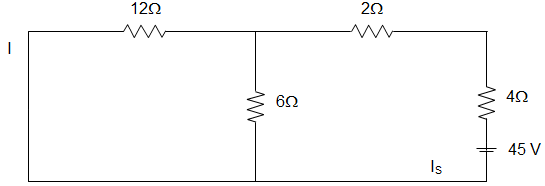
a) 1.5 A
b) 2.5 A
c) 3.5 A
d) 4.5 A
View Answer
Explanation: Equivalent resistance, REQ = [(12 || 6) + 2 + 4] = 10 Ω
IS = \(\frac{45}{10}\) = 4.5 A
Now, by using Current division rule, we get, I = \(\frac{4.5 × 6}{12+6} = \frac{27}{18}\) = 1.5 A.
6. A circuit is given in the figure below. We can infer that ________
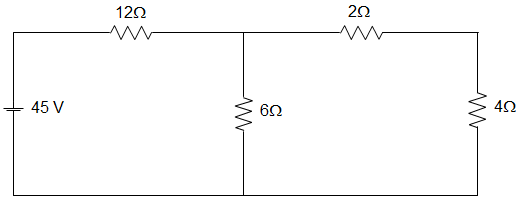
a) The circuit follows Reciprocity Theorem
b) The circuit follows Millman’s Theorem
c) The circuit follows Superposition Theorem
d) The circuit follows Tellegen Theorem
View Answer
Explanation: Let us consider this circuit,
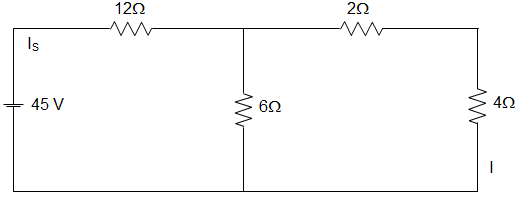
Rth = [(2+4) || 6] + 12 = 15 Ω
IS = \(\frac{45}{15}\) = 3 A
Now, by current division rule, we get, I1 = \(\frac{3 × 6}{12} = \frac{18}{12}\) = 1.5 A.
Again, let us consider this circuit,
![Equivalent resistance, REQ = [(12 || 6) + 2 + 4] = 10 Ω in given circuit](https://www.sanfoundry.com/wp-content/uploads/2019/08/network-theory-questions-answers-advanced-problems-reciprocity-theorem-q6b.png)
Equivalent resistance,REQ = [(12 || 6) + 2 + 4] = 10 Ω
IS = \(\frac{45}{10}\) = 4.5 A
Now, by using Current division rule, we get, I2 = \(\frac{4.5 × 6}{12+6} = \frac{27}{18}\) = 1.5 A.
Since I1 = I2, the circuit follows Reciprocity Theorem.
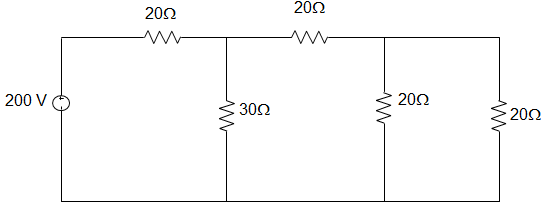
7. In the circuit given below, the current in the resistance 20 Ω(far end) is _________
a) 8.43 A
b) 5.67 A
c) 1.43 A
d) 2.47 A
View Answer
Explanation: Equivalent Resistance REQ = 20 + [30 || (20 + (20||20))]
= 20 + [30 || (20 + \(\frac{20×20}{20+20}\))]
= 20 + [30 || (20+10)]
= 20 + [30 || 30]
= 20 + \(\frac{30 × 30}{30+30}\)
= 20 + 15 = 35 Ω
The current drawn by the circuit = \(\frac{200}{35}\) = 5.71 A
Now, by using current division rule, we get, I2Ω = 1.43 A.
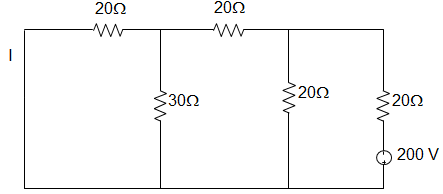
8. In the circuit given below, the value of I is __________
a) 2.47 A
b) 5.67 A
c) 8.43 A
d) 1.43 A
View Answer
Explanation: Equivalent Resistance, REQ = [[((30 || 20) + 20) || 20] + 20]
= \(\Big[\Big[\left(\left(\frac{30 × 20}{30+20}\right) + 20\right) || 20\Big] + 20\Big]\)
= [[(12 + 20) || 20] + 20]
= [[32 || 20] + 20]
= \(\Big[\left(\frac{32 × 20}{32+20}\right) + 20\Big]\)
= [12.31 + 20] = 32.31 Ω
The current drawn by the circuit = \(\frac{200}{32.31}\) = 6.19 A
Now, by using current division rule, we get, I2Ω = 1.43 A.
9. A circuit is given in the figure below. We can infer that ________

a) The circuit follows Reciprocity Theorem
b) The circuit follows Millman’s Theorem
c) The circuit follows Superposition Theorem
d) The circuit follows Tellegen Theorem
View Answer
Explanation: Let us consider this circuit,

Equivalent Resistance REQ = 20 + [30 || (20 + (20||20))] = 20 + [30 || (20 + \(\frac{20×20}{20+20}\))]
= 20 + [30 || (20+10)]
= 20 + [30 || 30]
= 20 + \(\frac{30 × 30}{30+30}\)
= 20 + 15 = 35 Ω
The current drawn by the circuit = \(\frac{200}{35}\) = 5.71 A
Now, by using current division rule, we get, I1 = 1.43 A
Again, let us consider this circuit,

Equivalent Resistance, REQ = [[((30 || 20) + 20) || 20] + 20]
= \(\Big[\Big[\left(\left(\frac{30 × 20}{30+20}\right) + 20\right) || 20\Big] + 20\Big]\)
= [[(12 + 20) || 20] + 20]
= [[32 || 20] + 20]
= \(\Big[\left(\frac{32 × 20}{32+20}\right) + 20\Big]\)
= [12.31 + 20] = 32.31 Ω
The current drawn by the circuit = \(\frac{200}{32.31}\) = 6.19 A
Now, by using current division rule, we get, I2 = 1.43 A.
Since I1 = I2, the circuit follows Reciprocity Theorem.
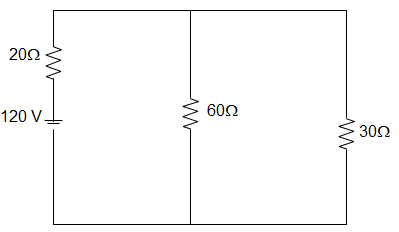
10. In the circuit given below, the current in the 30 Ω resistor is _________
a) 1 A
b) 2 A
c) 3 A
d) 4 A
View Answer
Explanation: Equivalent Resistance, REQ = 20 + [60 || 30]
= 20 + \(\frac{60 × 30}{60+30}\)
= 20 + 20 = 40 Ω
Total current from the source, I = \(\frac{120}{40}\) = 3A
Now, by using current division rule, I3Ω = \(\frac{3 × 60}{30+60}\) = 2 A.
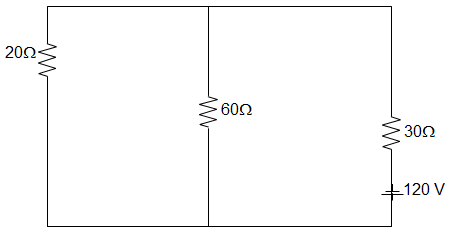
11. In the circuit given below, the current in the 20 Ω resistor is _________
a) 5 A
b) 1 A
c) 1.5 A
d) 2 A
View Answer
Explanation: Equivalent resistance, REQ = [[20 || 60] + 30]
= \(\Big[\frac{20 × 60}{20+60} + 30\Big]\)
= [15 + 30] = 45 Ω
Total current = \(\frac{120}{45}\) = 2.67 A
Current through the 20Ω resistor is, I20Ω = \(\frac{2.67 × 60}{60+20}\) = 2 A.
12. A circuit is given in the figure below. We can infer that ________

a) The circuit follows Reciprocity Theorem
b) The circuit follows Millman’s Theorem
c) The circuit follows Superposition Theorem
d) The circuit follows Tellegen Theorem
View Answer
Explanation: Let us consider this circuit,

Equivalent Resistance, Equivalent Resistance, REQ = 20 + [60 || 30]
= 20 + \(\frac{60 × 30}{60+30}\)
= 20 + 20 = 40 Ω
Total current from the source, I = \(\frac{120}{40}\) = 3A
Now, by using current division rule, I1 = \(\frac{3 × 60}{30+60}\) = 2 A.
Again, let us consider this circuit,

Equivalent resistance, REQ = [[20 || 60] + 30]
= \(\Big[\frac{20 × 60}{20+60} + 30\Big]\)
= [15 + 30] = 45 Ω
Total current = \(\frac{120}{45}\) = 2.67 A
Current through the 20Ω resistor is, I2 = \(\frac{2.67 × 60}{60+20}\) = 2 A
Since I1 = I2, the circuit follows Reciprocity Theorem.
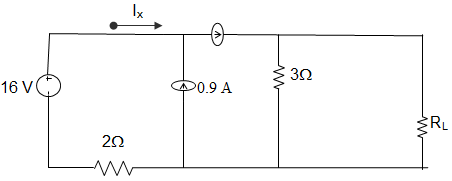
13. In the circuit given below, the value of load RL, for which maximum power is transferred through it is ___________
a) 2 Ω
b) 3 Ω
c) 1 Ω
d) 6 Ω
View Answer
Explanation: I + 0.9 = 10 I
Or, I = 0.1 A
VOC = 3 × 10 I = 30 I
Or, VOC = 3 V
Now, ISC = 10 I = 1 A
Rth = 3/1 = 3 Ω.
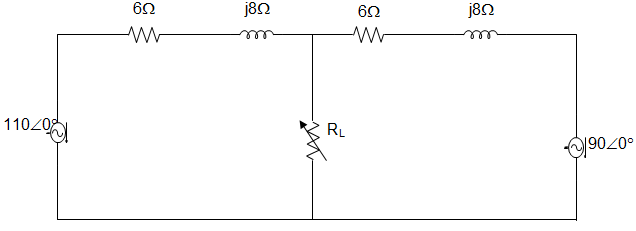
14. In the circuit given below, the maximum power absorbed by the load resistance RL is ___________
a) 2200 W
b) 1250 W
c) 1000 W
d) 621 W
View Answer
Explanation: RL = \(\sqrt{R_{TH}^2+X_{TH}^2}\)
= \(\sqrt{3^2+4^2}\) = 5
Now, 110 = (6 + j8 + 5) I1 + 5I2
And 90 = (6 + j8 + 5) I2 = 5I1
∴ I1 = 5.5 – 2.75j and I2 = 4.5 – 2.2j
Total current in RL = I1 + I2 = (10 – 4.95j) A = 11.15 A
∴ Power absorbed by RL = I2R
= 11.152 × 5 = 621 W.
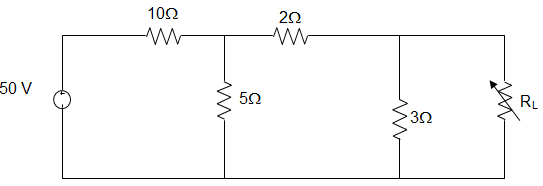
15. In the circuit given below, the maximum power delivered to the load is ___________
a) 3 W
b) 5.2 W
c) 3.2 W
d) 4.2 W
View Answer
Explanation: Equivalent resistance of the circuit is = [{(3 + 2) || 5} + 10] = (2.5 + 10) = 12.5 Ω
Total current drawn by the circuit is IT = \(\frac{50}{12.5}\) = 4 A
Current in 3 Ω resistor is I3 = IT × \(\frac{5}{5+5} = \frac{4 × 5}{10}\) = 2 A
VTH = V3 = 3 × 2 = 6V
RTH = RAB = [(2 + 5) || 3] = 2.1 Ω
For maximum power transfer RL = RTH = 2.1 Ω
∴ Current drawn by RL is IL = \(\frac{6}{2.1+2.1} = \frac{6}{4.2}\) = 1.42 A
∴ Power delivered to the load = \(I_L^2 R_L\)
= (1.42)2(2.1) = 4.2 W.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
