This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Circuit Elements in the S-Domain”.
1. The resistance element __________ while going from the time domain to frequency domain.
a) does not change
b) increases
c) decreases
d) increases exponentially
View Answer
Explanation: The s-domain equivalent circuit of a resistor is simply resistance of R ohms that carries a current I ampere seconds and has a terminal voltage V volts-seconds. The resistance element does not change while going from the time domain to the frequency domain.
2. The relation between current and voltage in the case of inductor is?
a) v=Ldt/di
b) v=Ldi/dt
c) v=dt/di
d) v=di/dt
View Answer
Explanation: Consider an inductor with an initial current Io. The time domain relation between current and voltage is v=Ldi/dt.
3. The s-domain equivalent of the inductor reduces to an inductor with impedance?
a) L
b) sL
c) s2L
d) s3L
View Answer
Explanation: If the initial energy stored in the inductor is zero, the equivalent circuit of the inductor reduces to an inductor with impedance sL ohms.
4. The voltage and current in a capacitor are related as?
a) i=Cdt/dv
b) v=Cdv/dt
c) i=Cdv/dt
d) v=Cdt/dv
View Answer
Explanation: Consider an initially charged capacitor and the initial voltage on the capacitor is Vo. The voltage current relation in the time domain is i=Cdv/dt.
5. The s-domain equivalent of the capacitor reduces to a capacitor with impedance?
a) sC
b) C
c) 1/C
d) 1/sC
View Answer
Explanation: The s-domain equivalent of the capacitor can be derived for the charged capacitor and it reduces to an capacitor with impedance 1/sC.
6. From the circuit shown below, find the value of current in the loop.

a) (V/R)/(s+1/RC)
b) (V/C)/(s+1/R)
c) (V/C)/(s+1/RC)
d) (V/R)/(s+1/R)
View Answer
Explanation: Applying Kirchhoff’s law around the loop, we have V/s=1/sC I+RI. Solving above equation yields I=CV/(RCS+1)=(V/R)/(s+1/RC).
7. After taking the inverse transform of current in the circuit shown below, the value of current is?

a) i=(V/C)e-t/R
b) i=(V/C)e-t/RC
c) i=(V/R)e-t/RC
d) i=(V/R)e-t/R
View Answer
Explanation: We had assumed the capacitor is initially charged to Vo volts. By taking the inverse transform of the current, we get i=(V/R) e-t/RC.
8. The voltage across the resistor in the circuit shown below is?

a) Vet/R
b) Ve-t/RC
c) Ve-t/R
d) Vet/RC
View Answer
Explanation: We can determine the voltage v by simply applying the ohm’s law from the circuit. And applying the Ohm’s law from the circuit v = Ri = Ve-t/RC.
9. The voltage across the resistor in the parallel circuit shown is?
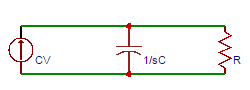
a) V/(s-1/R)
b) V/(s-1/RC)
c) V/(s+1/RC)
d) V/(s+1/C)
View Answer
Explanation: The given circuit is converted to parallel equivalent circuit. By taking the node equation, we get v/R+sCv=CV. Solving the above equation, v=V/(s+1/RC).
10. Taking the inverse transform of the voltage across the resistor in the circuit shown below is?

a) Ve-t/τ
b) Vet/τ
c) Vetτ
d) Ve-tτ
View Answer
Explanation: By taking the inverse transform, we get v=Ve-t/RC=Ve-t/τ, where τ is the time constant and τ = RC. And v is the voltage across the resistor.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
