This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Network Function for the One-Port and Two-Port”.
1. The ratio of voltage transform at first port to the voltage transform at the second port is called?
a) Voltage transfer ratio
b) Current transfer ratio
c) Transfer impedance
d) Transfer admittance
View Answer
Explanation: Voltage transfer ratio is the ratio of voltage transform at first port to the voltage transform at the second port and is denoted by G(s). G21 = V2(s)/V1(s) G12 = V1(s)/V2(s).
2. The ratio of the current transform at one port to current transform at other port is called?
a) Transfer admittance
b) Transfer impedance
c) Current transfer ratio
d) Voltage transfer ratio
View Answer
Explanation: Current transfer ratio is the ratio of the current transform at one port to current transform at other port and is denoted by α(s). α12(s) = I1(s)/I2(s) α21(s) = I2(s)/I1(s).
3. The ratio of voltage transform at the first port to the current transform at the second port is called?
a) Voltage transfer ratio
b) Transfer admittance
c) Current transfer ratio
d) Transfer impedance
View Answer
Explanation: Transfer impedance is the ratio of voltage transform at first port to the current transform at the second port and is denoted by Z(s). Z21(s) = V2(s)/I1(s) Z12(s) = V1(s)/I2(s).
4. For the network shown in the figure, find the driving point impedance.
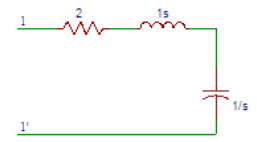
a) (s2-2s+1)/s
b) (s2+2s+1)/s
c) (s2-2s-1)/s
d) (s2+2s-1)/s
View Answer
Explanation: Applying Kirchoff’s law at port 1, Z(S)=V(S)/I(S), where V(s) is applied at port 1 and I(s) is current flowinmg through the network. Then Z(S)=V(S)/I(S) = 2+S+1/S = (s2+2s+1)/s.
5. Obtain the transfer function G21 (S) in the circuit shown below.
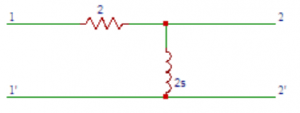
a) (s+1)/s
b) s+1
c) s
d) s/(s+1)
View Answer
Explanation: Applying Kirchhoff’s law V1 (S) = 2 I1 (S) + 2 sI1 (S) V2 (S) = I1 (S) X 2s Hence G21 (S) = V2(s)/V1(s) = 2 s/(2+2 s)=s/(s+1).
6. Determine the transfer function Z21 (S) in the circuit shown below.

a) s
b) 2 s
c) 3 s
d) 4 s
View Answer
Explanation: The transfer function Z21 (S) is Z21 (S) = V2(S)/I1(S). V2 (S) = I1 (S) X 2s. V2(S)/I1(S)=2s. On substituting Z21 (S) = 2s.
7. Find the driving point impedance Z11 (S) in the circuit shown below.

a) 2(s+2)
b) (s+2)
c) 2(s+1)
d) (s+1)
View Answer
Explanation: The driving point impedance Z11 (S) is Z11 (S)=V1(S)/I1(S). V1 (S) = 2 I1 (S) + 2 sI1 (S) => V1(S) = (2+2s)I1(S) => V1(S)/I1(S) = 2(s+1). On substituting Z11 (S) = 2(S+1).
8. Obtain the transfer function G21 (s) in the circuit shown below.
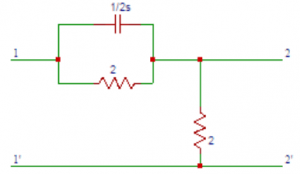
a) (8 S+2)/(8 S+1)
b) (8 S+2)/(8 S+2)
c) (8 S+2)/(8 S+3)
d) (8 S+2)/(8 S+4)
View Answer
Explanation: From the circuit, the parallel combination of resistance and capacitance can be combined into equivalent in impedance. Zeq(S) = 1/(2 S+1/2)=2/(4 S+1). Applying Kirchhoff’s laws, we have V2 (S) = 2 I1(S) => V1 (S) = I1 (S)[2/(4 S+1)+2] = I1 (S)[(8 S+4)/(4 S+1)] The transfer function G21 (s) = V2(s)/V1(s) = 2 I1(S)/((8 S+4)/(4 S+1))I1(S) = (8 S+2)/(8 S+4).
9. Obtain the transfer function Z21(s) in the circuit shown below.

a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The transfer function Z21(s) is Z21 (S) = V2(S)/I1(S). V2 (S) = 2 I1(S) => V2 (S)/I1 = 2. On substituting Z21(s) = 2.
10. Determine the driving point impedance Z11(S) in the circuit shown below.

a) (8 S+4)/(4 S+4)
b) (8 S+4)/(4 S+3)
c) (8 S+4)/(4 S+2)
d) (8 S+4)/(4 S+1)
View Answer
Explanation: The driving point impedance Z11(S) is Z11(S) = V1(s)/I1(s). V1(s) = I1(s)((2/(4s+1))+2) = I1(s)((8s+4)/(4s+1)) => V1(s)/I1(s) = ((8s+4)/(4s+1)). On substituting we get Z11(S) = (8S+4)/(4S+1).
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Electrical Engineering MCQs
- Apply for Electronics & Communication Engineering Internship
- Check Electrical Engineering Books
- Apply for Electrical Engineering Internship
- Practice Electronics & Communication Engineering MCQs
