This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “m-Derived T-Section”.
1.The relation between ZoT and ZoT‘ in the circuits shown below.
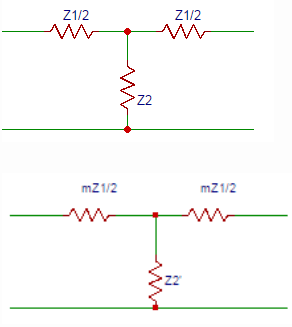
a) ZoT = ZoT‘
b) ZoT = 2 ZoT‘
c) ZoT = 3 ZoT‘
d) ZoT = 4 ZoT‘
View Answer
Explanation: The relation between ZoT and ZoT’ is ZoT = ZoT’ where ZoT’ is the characteristic impedance of the modified (m-derived) T-network.
2. The value of Z2’ in terms of Z1, Z2 from the circuits shown below is?

a) Z2‘=Z2/4 m (1-m2)+Z2/m
b) Z2‘=Z1/4 m (1-m2)+Z1/m
c) Z2‘=Z2/4 m (1-m2)+Z1/m
d) Z2‘=Z1/4 m (1-m2)+Z2/m
View Answer
Explanation: As ZoT = ZoT’, √(Z12/4+Z1Z2)=√(m2 Z12/4+m Z2‘). On solving, Z2‘=Z1/(4 m (1-m2))+Z2/m.
3. The relation between Zoπ and Zoπ’ in the circuits shown below is?
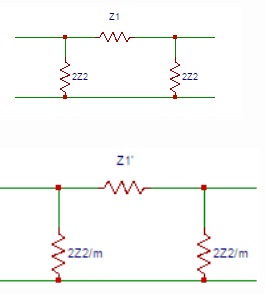
a) Zoπ = 2 Zoπ’
b) Zoπ = 4 Zoπ’
c) Zoπ = Zoπ’
d) Zoπ = 3 Zoπ’
View Answer
Explanation: The characteristic impedances of the prototype and its modified sections have to be equal for matching. The relation between Zoπ and Zoπ‘ is Zoπ = Zoπ’.
4. The value of Z1‘ in terms of Z1, Z2 from the circuits shown below is?

a) Z1‘=(m Z2(Z2 4 m)/(1-m2))/m Z1(Z2 4 m/(1-m2))
b) Z1‘=(m Z1(Z2 4 m)/(1-m2))/m Z2(Z2 4 m/(1-m2))
c) Z1‘=(m Z1(Z2 4 m)/(1-m2))/m Z1(Z2 4 m/(1-m2))
d) Z1‘=(m Z1(Z2 4 m)/(1-m2))/m Z1(Z1 4 m/(1-m2))
View Answer
Explanation: As Zoπ = Zoπ’, √(Z1Z2/(1+Z1/4 Z2))=√(((Z1‘ Z2)/m)/(1+(Z1‘)/(4 Z2/m))). On solving, Z1‘=(m Z1(Z2 4 m)/(1-m2))/m Z1(Z2 4 m/(1-m2)).
5. The value of resonant frequency in the m-derived low pass filter is?
a) fr=1/(√(LC(1+m2)))
b) fr=1/(√(πLC(1+m2)))
c) fr=1/(√(LC(1-m2)))
d) fr=1/(√(πLC(1-m2)))
View Answer
Explanation: ωr2 = 1/(LC(1-m2)). So the value of resonant frequency in the m-derived low pass filter is fr=1/√(πLC(1-m2)).
6. The cut-off frequency of the low pass filter is?
a) 1/√LC
b) 1/(π√LC)
c) 1/√L
d) 1/(π√L)
View Answer
Explanation: To determine the cut-off frequency of the low pass filter we place m = 0. So fc=1/(π√LC).
7. The resonant frequency of m-derived low pass filter in terms of the cut-off frequency of low pass filter is?
a) fc/√(1-m2)
b) fc/√(1+m2)
c) fc/(π√(1-m2))
d) fc/(π√(1+m2))
View Answer
Explanation: If a sharp cut-off is desired, the frequency at infinity should be near to fc. The resonant frequency of m-derived low pass filter in terms of the cut-off frequency of low pass filter is fr=fc/√(1-m2).
8. The expression of m of the m-derived low pass filter is?
a) m=√(1+(fc/fr)2)
b) m=√(1+(fc/f)2)
c) m=√(1-(fc/fr)2)
d) m=√(1-(fc/f)2)
View Answer
Explanation: As fr=fc/√(1-m2). The expression of m of the m-derived low pass filter is m=√(1-(fc/fr)2).
9. Given a m-derived low pass filter has cut-off frequency 1 kHz, design impedance of 400Ω and the resonant frequency of 1100 Hz. Find the value of k.
a) 400
b) 1000
c) 1100
d) 2100
View Answer
Explanation: The value of k is equal to the design impedance. Given design impedance is 400Ω. So, k = 400.
10. Given a m-derived low pass filter has cut-off frequency 1 kHz, design impedance of 400Ω and the resonant frequency of 1100 Hz. Find the value of m.
a) 0.216
b) 0.316
c) 0.416
d) 0.516
View Answer
Explanation: m=√(1-(fc/fr)2) fc = 1000, fr = 1100. On substituting m=√(1-(1000/1100)2)=0.416.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
