This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Reciprocity Theorem”.
1. To check for the Reciprocity Theorem we consider ______ of response to excitation.
a) ratio
b) addition
c) product
d) subtraction
View Answer
Explanation: For the Reciprocity Theorem to satisfy the ratio of response to the excitation of the circuit should be equal to the ratio of response to excitation after the source is replaced.
2. For the Reciprocity Theorem to satisfy the ratio of response to excitation before and after the source is replaced should be?
a) different
b) same
c) before source is replaced is greater than after the source is replaced
d) before source is replaced is less than after the source is replaced
View Answer
Explanation: For the Reciprocity Theorem to satisfy the ratio of response to excitation before and after the source is replaced should be same and if that condition satisfies the reciprocity theorem is valid for the given circuit.
3. The circuit which satisfies Reciprocity Theorem is called?
a) Short circuit
b) Open circuit
c) Linear circuit
d) Non-linear circuit
View Answer
Explanation: The circuit which satisfies Reciprocity Theorem is called linear circuit. A linear circuit is an electronic circuit in which, for a sinusoidal input voltage of frequency f, any steady-state output of the circuit (the current through any component, or the voltage between any two points) is also sinusoidal with frequency f.
4. Find the current through the 2Ω(c-d) resistor in the circuit shown below.
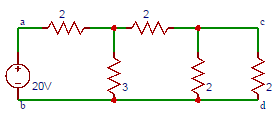
a) 0.143
b) 1.43
c) 14.3
d) 143
View Answer
Explanation: Total resistance in the circuit = 2+[3||(2+2│├|2)]=3.5Ω. The current drawn by the circuit (It)=20/3.5=5.71Ω. The current drawn by 2Ω resistor = 1.43A.
5. In the following circuit, the current drawn by 2Ω resistor (a-b) after the source is replaced is?

a) 143
b) 14.3
c) 1.43
d) 0.143
View Answer
Explanation: The circuit after the source is replaced is
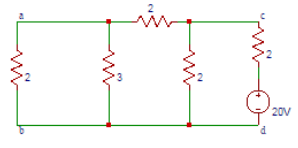
Total resistance = 3.23Ω. The current drawn by the circuit (It)=20/3.23=6.19A. The current in branch a-b is 1.43A.
6. The following circuit satisfies Reciprocity Theorem.

a) True
b) False
View Answer
Explanation: The ratio of response to excitation before the source is replaced is equal to 0.0715. And the ratio of response to excitation before the source is replaced is equal to 0.0715. So, the circuit satisfies the Reciprocity theorem.
7. Find the current through 3Ω resistor in the circuit shown below.
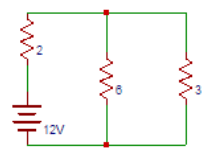
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The 6Ω resistor is parallel to 3Ω resistor and the resultant is in series with 2Ω resistor. Total current from source = 12/(2+(6│|3))=3A. Current through 3Ω resistor = 3 × 6/(6+3)=2A.
8. Find the current through 2Ω resistor after source is replaced in the below circuit.

a) 4
b) 3
c) 2
d) 1
View Answer
Explanation: The circuit after source is replaced is
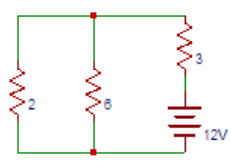
Total current from the source (It)=12/(3+(6│|2))=2.67A. Current through 2Ω resistor=2.67× 6/(6+2)=2A.
9. The following circuit satisfies the reciprocity theorem.

a) False
b) True
View Answer
Explanation: The ratio of response to excitation before the source is replaced is equal to 0.167. And the ratio of response to excitation before the source is replaced is equal to 0.167. So, the circuit satisfies the Reciprocity theorem.
10. While considering Reciprocity theorem, we consider ratio of response to excitation as ratio of?
a) voltage to voltage
b) current to current
c) voltage to current
d) none of the mentioned
View Answer
Explanation: While considering Reciprocity theorem, we consider ratio of response to excitation as ratio of voltage to current or current to voltage.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
