This set of Network Theory online quiz focuses on “Series and Parallel Combination of Elements”.
1. In the circuit shown below, switch K is moved from position to position 2 at time t = 0. At time t = 0-, the current in the inductor is I0 and the voltage at the capacitor is V0. The inductor is represented by a transform impedance _________ in series with a voltage source __________
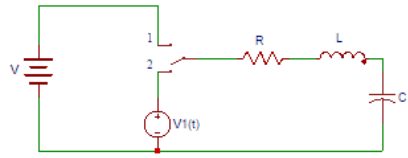
a) Ls, L V0
b) Ls, LI0
c) 1/Ls, LI0
d) 1/Ls, L V0
View Answer
Explanation: The inductor has an initial current I0. It is represented by a transform impedance Ls in series with a voltage source L V0.
2. In the circuit shown below, the capacitor is replaced by a transform impedance of __________ with an initial voltage ___________

a) 1/Cs, V0/S
b) 1/Cs, I0/S
c) Cs, I0/S
d) Cs, V0/S
View Answer
Explanation: The capacitor has an initial voltage V0 across it. It is represented by a transform impedance of 1/Cs with an initial voltage V0/S.
3. The value of the total voltage after replacing the inductor and capacitor is?

a) V1(S)-LI0-V0/S
b) V1(S)+LI0-V0/S
c) V1(S)+LI0+V0/S
d) V1(S)-LI0+V0/S
View Answer
Explanation: The current I(s) is given as the total transform voltage in the circuit divided by the total transform impedance. The value of the total voltage after replacing the inductor and capacitor is V (s) = V1(S)+LI0-V0/S.
4. The value of the total impedance after replacing the inductor and capacitor is?

a) R-LS-1/CS
b) R-LS+1/CS
c) R+LS+1/CS
d) R+LS-1/CS
View Answer
Explanation: The value of the total impedance after replacing the inductor and capacitor is Z (s) = R+LS+1/CS. By knowing the V(s) and Z(s) we can calculate I(s) as I(s) is given as the total transform voltage in the circuit divided by the total transform impedance.
5. The current flowing in the following circuit is?

a) (V1(S)-LI0-V0/S)/(R+LS+1/CS)
b) (V1(S)-LI0+V0/S)/(R+LS+1/CS)
c) (V1(S)+LI0+V0/S)/(R+LS+1/CS)
d) (V1(S)+LI0-V0/S)/(R+LS+1/CS)
View Answer
Explanation: The current I(s) is given as the total transform voltage in the circuit divided by the total transform impedance. The current flowing in the circuit is I (s) = V(s)/I(s) = (V1(S)+LI0-V0/S)/(R+LS+1/CS).
6. Obtain the admittance of the last two elements in the parallel combination after transformation in the circuit shown below.
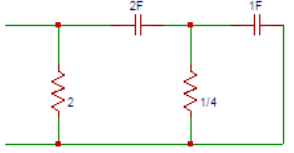
a) 1+s
b) 2+s
c) 3+s
d) 4+s
View Answer
Explanation: The term admittance is defined as the inverse of impedance. The admittance of capacitor is 1/s and the admittance of resistor is 1/4 mho. So the admittance of the last two elements in the parallel combination is Y1(s) = 4 + s.
7. The impedance of the last two elements in the parallel combination after transformation in the circuit shown below is?

a) 1/(s+4)
b) 1/(s+3)
c) 1/(s+2)
d) 1/(s+1)
View Answer
Explanation: The impedance of resistor is 4Ω and the impedance of capacitor is s. So the impedance of the last two elements in the parallel combination is Z1(s) = 1/(s+4).
8. The series combination of the last elements after replacing 1/s and 1/4Ω with 1/(S+4) is?

a) (3s+4)/2s(s-4)
b) (3s-4)/2s(s-4)
c) (3s+4)/2s(s+4)
d) (3s-4)/2s(s+4)
View Answer
Explanation: We got the impedance of last two elements in parallel combination as Z1(s) = 1/(s+4) and now the impedance of capacitor is 1/2s. So the series combination of the last elements is Z2(s) = 1/2s+1/(s+4) = (3s+4)/2s(s+4).
9. Determine the admittance parallel combination of the last elements after replacing with (3s+4)/2s(s+4) is?

a) (4s2-19s+4)/(6s-8)
b) (4s2+19s-4)/(6s+8)
c) (4s2+19s-4)/(6s-8)
d) (4s2+19s+4)/(6s+8)
View Answer
Explanation: The term admittance is defined as the inverse of the term impedance. As the impedance is Z2(s) = 1/2s+1/(s+4)=(3s+4)/2s(s+4), the admittance parallel combination of the last elements is Y2(s) = 1/2+2s(s+4)/(3s+4)=(4s2+19s+4)/(6s+8).
10. Obtain the transform impedance of the network shown below.

a) (6s-8)/(4s2+19s-4)
b) (6s+8)/(4s2+19s+4)
c) (6s+8)/(4s2-19s+4)
d) (6s-8)/(4s2+19s+4)
View Answer
Explanation: The term impedance is the inverse of the term admittance. We got admittance as Y2(s) = (4s2+19s+4)/(6s+8). So the transform impedance of the network is
Z (s) = 1/Y2(s) = (6s+8)/(4s2+19s+4).
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory for online Quizzes, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Network Theory Books
- Practice Electronics & Communication Engineering MCQs
- Check Electronics & Communication Engineering Books
- Apply for Electrical Engineering Internship
- Practice Electrical Engineering MCQs
