This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Supernode Analysis”.
1. Consider the figure shown below. Find the voltage (V) at node 1.
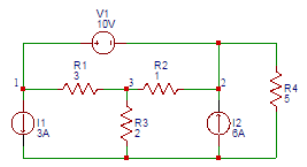
a) 13
b) 14
c) 15
d) 16
View Answer
Explanation: Applying Super Node Analysis, the combined equation of node 1 and node 2 is (V1-V3)/3+3+(V2-V3)/1-6+V2/5=0. At node 3, (V3-V1)/3+(V3-V2)/1+V3/2=0. Also V1-V2=10. On solving above equations, we get V1 = 13.72V ≈ 14V.
2. Consider the figure shown below. Find the voltage (V) at node 2.
a) 3
b) 4
c) 5
d) 6
View Answer
Explanation: Applying Super Node Analysis, the combined equation of node 1 and node 2 is (V1-V3)/3+3+(V2-V3)/1-6+V2/5=0. At node 3, (V3-V1)/3+(V3-V2)/1+V3/2=0. Also V1-V2=10. On solving above equations, we get V2 = 3.72V ≈ 4V.
3. Consider the figure shown below. Find the voltage (V) at node 3.
a) 4.5
b) 5.5
c) 6.5
d) 7.5
View Answer
Explanation: Applying Super Node Analysis, the combined equation of node 1 and node 2 is (V1-V3)/3+3+(V2-V3)/1-6+V2/5=0. At node 3, (V3-V1)/3+(V3-V2)/1+V3/2=0. Also V1-V2=10. On solving above equations, we get V3 = 4.5V.
4. Consider the figure shown below. Find the power (W) delivered by the source 6A.
a) 20.3
b) 21.3
c) 22.3
d) 24.3
View Answer
Explanation: The term power is defined as the product of voltage and current and the power delivered by the source (6A) = V2x6 = 3.72×6 = 22.32W.
5. Find the voltage (V) at node 1 in the circuit shown below.
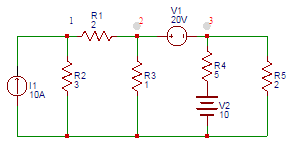
a) 18
b) 19
c) 20
d) 21
View Answer
Explanation: The equation at node 1 is 10 = V1/3+(V1-V2)/2. According to super Node analysis, (V1-V2)/2=V2/1+(V3-10)/5+V3/2V2-V3=20. On solving, we get, V1=19V.
6. Consider the figure shown below. Find the voltage (V) at node 2.
a) 11.5
b) 12
c) 12.5
d) 13
View Answer
Explanation: The equation at node 1 is 10 = V1/3+(V1-V2)/2
According to super Node analysis, (V1-V2)/2=V2/1+(V3-10)/5+V3/2V2-V3=20. On solving, we get, V2=11.5V.
7. Find the voltage (V) at node 3 in the figure shown below.
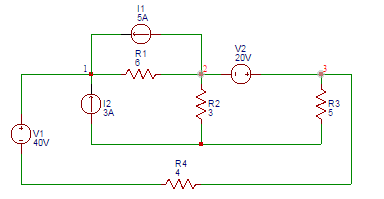
a) 18
b) 20
c) 22
d) 24
View Answer
Explanation: At node 1, (V1-40-V3)/4+(V1-V2)/6-3-5=0. Applying Super Node Analysis at node 2 and 3, (V2-V1)/6+5+V2/3+V3/5+(V3+40-V1)/4=0. Also, V3-V2=20. On solving above equations, V3 = 18.11V ≈ 18V.
8. Find the power absorbed by 5Ω resistor in the following figure.
a) 60
b) 65.5
c) 70.6
d) 75
View Answer
Explanation: The current through 5Ω resistor = V3/5=18.11/5=3.62A. The power absorbed by 5Ω resistor = (3.62)2)×5=65.52W.
9. Find the value of the voltage (V) in the equivalent voltage source of the current source shown below.
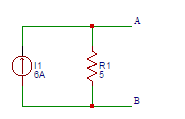
a) 20
b) 25
c) 30
d) 35
View Answer
Explanation: The value of the voltage (V) in the equivalent voltage source of the current source the voltage across the terminals A and B is (6)(5) = 30V.
10. Find the value of the current (A) in the equivalent current source of the voltage source shown below.
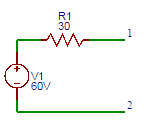
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The value of the current (A) in the equivalent current source of the voltage source the short circuit current at the terminals A and B is I=60/30=2A.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
