This set of Network Theory Questions & Answers for Exams focuses on “Problems of Series Resonance Involving Frequency Response of Series Resonant Circuit”.
1. A series RLC circuit has R = 50 Ω, L = 0.01 H and C = 0.04 × 10-6 F. System voltage is 100 V. The frequency, at which the maximum voltage appears across the capacitor, is?
a) 5937.81 Hz
b) 7370 Hz
c) 7937.81 Hz
d) 981 Hz
View Answer
Explanation: Frequency fc at which VC is maximum fc = \(\frac{1}{2π}\Big[\frac{1}{0.01×0.01×10^{-6}} – \frac{50×50}{2×0.01×0.01}\Big]^{0.5}\)
So, fc = 7937.81 Hz.
2. A series RLC circuit has R = 50 Ω, L = 0.01 H and C = 0.04 × 10-6 F. System voltage is 100 V. At this frequency, the circuit impedance is?
a) 50 – j2.5 Ω
b) 50 – j2.8 Ω
c) 50 + j2.5 Ω
d) 50 + j2.8 Ω
View Answer
Explanation: Z = R + j (ωL + \(\frac{1}{ωC}\)) = 50 + j \(\left(2π × 7937.81 × 0.01 – \frac{1}{2π×7937.81×0.04×10^{-6}}\right)\) = 50 – j2.5 Ω.
3. Given, R = 10 Ω, L = 100 mH and C = 10 μF. The values of ω0, ω1 and ω2 respectively are?
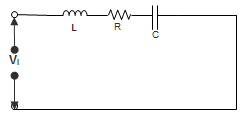
a) ω0 = 1000 rad/s, ω1 = 951.25 rad/s, ω2 = 1075.54 rad/s
b) ω0 = 1000 rad/s, ω1 = 975.25 rad/s, ω2 = 1051.25 rad/s
c) ω0 = 1000 rad/s, ω1 = 951.25 rad/s, ω2 = 1051.25 rad/s
d) ω0 = 1000 rad/s, ω1 = 825.30 rad/s, ω2 = 1075.54 rad/s
View Answer
Explanation: ω0 = \(\frac{1}{\sqrt{100×10^{-3}×10×10^{-6}}}\) = 1000 rad/s
Now, ω1 = \(\frac{-R + \sqrt{R^2 + \frac{4L}{C}}}{2L} = \frac{-10 + \frac{\sqrt{100 + 4 × 100 × 10^{-3}}}{10×10^{-6}}}{2×100×10^{-3}}\) = 951.25 rad/s
And, ω2 = \(\frac{+R+ \sqrt{R^2+ 4L/C}}{2L}\) = 1051.25 rad/s.
4. Given, R = 10 Ω, L = 100 mH and C = 10 μF. Selectivity is?

a) 10
b) 1.2
c) 0.15
d) 0.1
View Answer
Explanation: Selectivity = \(\frac{1}{Q}\)
Q = \(\frac{ωL}{R} = \frac{1000×100×10^{-3}}{10}\)
∴ Q = 10
So, Selectivity = 0.1.
5. Two series resonant filters are shown below. Let the 3 dB bandwidth of filter 1 be B1 and that of filter 2 be B2. The value of \(\frac{B_1}{B_2}\) is ____________
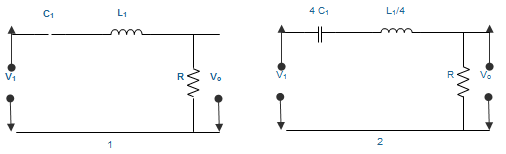
a) 0.25
b) 1
c) 0.5
d) 0.75
View Answer
Explanation: For series resonant circuit, 3dB bandwidth is \(\frac{R}{L}\)
B1 = \(\frac{R}{L_1}\)
B2 = \(\frac{R}{L_2} = \frac{4R}{L_1}\)
Hence, \(\frac{B_1}{B_2}\) = 0.25.
6. A 440 V, 50 HZ AC source supplies a series LCR circuit with a capacitor and a coil. If the coil has 100 mΩ resistance and 15 mH inductance, then at a resonance frequency of 50 Hz, the half power frequencies of the circuit are?
a) 50.53 Hz, 49.57 Hz
b) 52.12 HZ, 49.8 Hz
c) 55.02 Hz, 48.95 Hz
d) 50 HZ, 49 Hz
View Answer
Explanation: Bandwidth, BW = \(\frac{f_o}{Q} = \frac{50}{47.115}\) = 1.061 Hz
f2, higher half power frequency = f0 + \(\frac{BW}{2}\)
∴ f2 = 50 + \(\frac{1.061}{2}\) =50.53 Hz
f1, lower half power frequency = f0 – \(\frac{BW}{2}\)
∴ f1 = 100 – \(\frac{1.59}{2}\) = 49.47 Hz.
7. At what frequency will the current lead the voltage by 30° in a series circuit with R = 10Ω and C = 25 μF?
a) 11.4 kHz
b) 4.5 kHz
c) 1.1 kHz
d) 24.74 kHz
View Answer
Explanation: From the impedance diagram, 10 – jXC = Z∠-30°
∴ – XC = 10 tan (-30°) = -5.77 Ω
∴ XC = 5.77 Ω
Then, XC = \(\frac{1}{2πfC}\) or, f = \(\frac{1}{2πX_C C}\) = 1103 HZ = 1.1 kHz.
8. A 440 V, 50 HZ AC source supplies a series LCR circuit with a capacitor and a coil. If the coil has 100 mΩ resistance and 15 mH inductance, then at a resonance frequency of 50 Hz, what is the value of the capacitor?
a) 676 μF
b) 575 μF
c) 591 μF
d) 610 μF
View Answer
Explanation: We know that fo = \(\frac{1}{2π\sqrt{LC}}\)
Or, 50 = \(\frac{1}{2π\sqrt{5×10^{-3}×C}}\)
Or, C = \(\frac{1}{4π^2×50^2×15×10^{-3}}\) ≈ 676 μF.
9. A 440 V, 50 HZ AC source supplies a series LCR circuit with a capacitor and a coil. If the coil has 100 mΩ resistance and 15 mH inductance, then at a resonance frequency of 50 Hz, the Q factor of the circuit is?
a) 82.63
b) 47.115
c) 27.38
d) 92.38
View Answer
Explanation: We know that, Q = \(\frac{ωL}{R}\)
Or, Q = \(\frac{2π×50×15×10^{-3}}{100×10^{-3}}\) = 47.115.
10. For the circuit given below, if the frequency of the source is 50 Hz, then a value of to which results in a transient free response is?
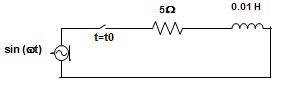
a) 0
b) 1.78 ms
c) 7.23 ms
d) 9.21 ms
View Answer
Explanation: For the ideal case, transient response will die out with time constant.
T = \(\frac{L}{R} = \frac{0.01}{5}\) = 0.002 s = 2 ms
Practically, T will be less than 2 ms.
11. In the circuit given below, the magnitudes of VL and VC are twice that of VK. Calculate the inductance of the coil, given that f = 50.50 Hz.
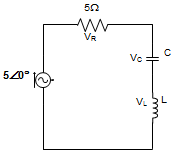
a) 6.41 mH
b) 5.30 mH
c) 3.18 mH
d) 2.31 mH
View Answer
Explanation: VL = VC = 2 VR
∴ Q = \(\frac{V_L}{V_R}\) = 2
But we know, Q = \(\frac{ωL}{R} = \frac{1}{ωCR}\)
∴ 2 = \(\frac{2πf × L}{5}\)
Or, L = 3.18 mH.
12. A circuit with a resistor, inductor and capacitor in series is resonant with frequency f Hz. If all the component values are now doubled, then the new resonant frequency will be?
a) 2 f
b) f
c) \(\frac{f}{4}\)
d) \(\frac{f}{2}\)
View Answer
Explanation: Resonance frequency = \(\frac{1}{2π\sqrt{LC}} = \frac{1}{2π2\sqrt{LC}}\)
Hence, \(\frac{f}{f_o} = \frac{\frac{1}{2π\sqrt{LC}}}{\frac{1}{2π2\sqrt{LC}}}\) = 2
∴ f = 2fo.
13. A series RLC circuit has a resonance frequency of 1 kHz and a quality factor Q = 50. If R and L are doubled and C is kept same, the new Q of the circuit is?
a) 25.52
b) 35.35
c) 45.45
d) 20.02
View Answer
Explanation: Quality factor Q of the series RLC circuit is given by, Q = \(\frac{1}{R} \sqrt{\frac{L}{C}}\)
Qnew = \(\frac{1}{2R} \sqrt{\frac{2L}{C}} = \frac{1}{2} × \frac{1}{R} \sqrt{\frac{2L}{C}} = \frac{1}{2} × \sqrt{2} × Q\) = 35.35.
14. In a series RLC circuit R = 10 kΩ, L = 0.5 H and C = \(\frac{1}{250}\) μF. Calculate the frequency when the circuit is in a state of resonance.
a) 4.089 × 104 Hz
b) \(\frac{11111.1}{π}\)Hz
c) 4.089π × 104 Hz
d) \(\frac{1}{π}\) × 104 Hz
View Answer
Explanation: Resonance frequency = \(\frac{1}{2π\sqrt{LC}}\)
= \(\frac{1}{2π\sqrt{\frac{1}{250} × 10^{-6} × 0.5}} = \frac{11111.1}{π}\)Hz.
15. In a series RLC circuit for lower frequency and for higher frequency, power factors are respectively ______________
a) Leading, Lagging
b) Lagging, Leading
c) Independent of Frequency
d) Same in both cases
View Answer
Explanation: A Leading power factor means that the current in the circuit leads the applied voltage. This condition occurs in capacitive circuits. On the other hand, a lagging power factor indicates that the current lags the voltage and this condition happens in an inductive circuit.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
