Two Port Network Advanced Problems Questions and Answers

This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Advanced Problems on Two Port Network – 1”.

1. For the circuit given below, the value of the z₁₂ parameter is ___________

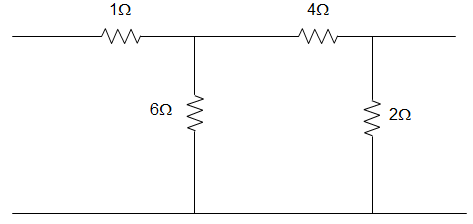
a) z₁₂ = 1 Ω
b) z₁₂ = 4 Ω
c) z₁₂ = 1.667 Ω
d) z₁₂ = 2.33 Ω
View Answer

Answer: a
Explanation: z₁₁ = \(\frac{V_1}{I_1}\) = 1 + 6 || (4+2) = 4Ω
I₀ = \(\frac{1}{2} I_1 \)
V₂ = 2I₀ = I₁
z₂₁ = \(\frac{V_2}{I_1}\) = 1Ω
z₂₂ = \(\frac{V_2}{I_2}\) = 2 || (4+6) = 1.667Ω
So, I’₀ = \(\frac{2}{2+10}I_2 = \frac{1}{6}I_2 \)
V₁ = 6I’₀ = I₂
z₁₂ = \(\frac{V_1}{I_2}\) = 1Ω
Hence, [z] = [4:1; 1:1.667] Ω.

2. For the network of figure, z₁₁ is equal to ___________

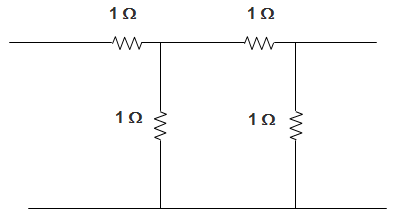
a) \(\frac{5}{3}\) Ω
b) \(\frac{3}{2}\) Ω
c) 2 Ω
d) \(\frac{2}{3}\) Ω
View Answer

Answer: a
Explanation: From the figure, we can infer that,
Z₁₁ = 1 + \(\frac{1 X 2}{3}\)
= 1 + \(\frac{2}{3}\)
= \(\frac{5}{3}\) Ω.

3. For the circuit given below, the value of z₁₁ parameter is ____________

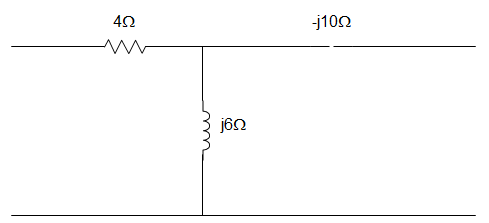
a) z₁₁ = 4 + j6 Ω
b) z₁₁ = j6 Ω
c) z₁₁ = -j6 Ω
d) z₁₁ = -j6 + 4 Ω
View Answer

Answer: a
Explanation: z₁₂ = j6 = z₂₁
z₁₁ – z₁₂ = 4
Or, z₁₁ = z₁₂ + 4 = 4 + j6 Ω
And z₂₂ – z₁₂ = -j10
Or, z₂₂ = z₁₂ + -j10 = -j4 Ω
∴ [z] = [4+j6:j6; j6:-j4] Ω.

4. In a series RLC circuit excited by a voltage 3e^-t u (t), the resistance is equal to 1 Ω and capacitance = 2 F. For the circuit, the values of I (0⁺) and I (∞), are ____________
a) 0 and 1.5 A
b) 1.5 A and 3 A
c) 3 A and 0
d) 3 A and 1.5 A
View Answer

Answer: c
Explanation: I(s) = \(\frac{6}{s+1} – \frac{3}{s+0.5}\)
Or, I(t) = 6 e^-t – 3 e^-0.5t
Putting, t = 0, we get, I(0) = 3A
Putting t = ∞, we get, I (∞) = 0.

5. For the circuit given below, the value of z₁₂ parameter is ____________

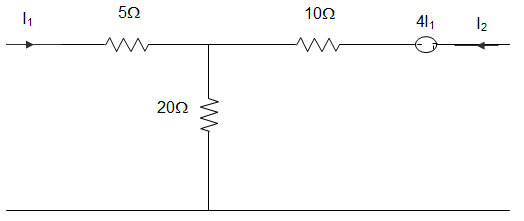
a) Z₁₂ = 20 Ω
b) Z₁₂ = 25 Ω
c) Z₁₂ = 30 Ω
d) z₁₂ = 24 Ω
View Answer

Answer: a
Explanation: z₁₁ = \(\frac{V_1}{I_1} = \frac{(20+5)I_1}{I_1}\) = 25Ω
V₀ = \(\frac{20}{25}\)V₁ = 20 I₁
-V₀ – 4I₂ + V₂ = 0
Or, V₂ = V₀ + 4I₁ = 20I₁ + 4I₁ = 24 I₁
Or, z₂₁ = \(\frac{V_2}{I_1}\) = 24 Ω
V₂ = (10+20) I₂ = 30 I₂
Or, z₂₂ = \(\frac{V_2}{I_1}\) = 30 Ω
V₁ = 20I₂
Or, z₁₂ = \(\frac{V_1}{I_2}\) = 20 Ω
∴ [z] = [25:20; 24:30] Ω.

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. For the circuit given below, the value of the z₂₂ parameter is ___________

a) z₂₂ = 1 Ω
b) z₂₂ = 4 Ω
c) z₂₂ = 1.667 Ω
d) z₂₂ = 2.33 Ω
View Answer

Answer: c
Explanation: z₁₁ = \(\frac{V_1}{I_1}\) = 1 + 6 || (4+2) = 4Ω
I₀ = \(\frac{1}{2} I_1 \)
V₂ = 2I₀ = I₁
z₂₁ = \(\frac{V_2}{I_1}\) = 1Ω
z₂₂ = \(\frac{V_2}{I_2}\) = 2 || (4+6) = 1.667Ω
So, I’₀ = \(\frac{2}{2+10}I_2 = \frac{1}{6}I_2 \)
V₁ = 6I’₀ = I₂
z₁₂ = \(\frac{V_1}{I_2}\) = 1Ω
Hence, [z] = [4:1; 1:1.667] Ω.

7. For the circuit given below, the value of z₂₂ parameter is ____________

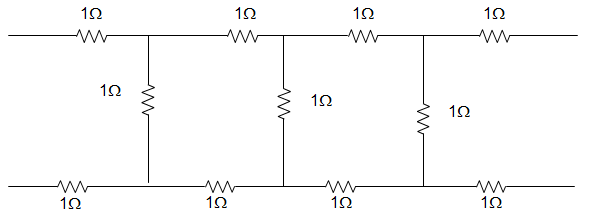
a) z₂₂ = 0.0667 Ω
b) z₂₂ = 2.773 Ω
c) z₂₂ = 1.667 Ω
d) z₂₂ = 0.999 Ω
View Answer

Answer: b
Explanation: z₁₁ = \(\frac{V_1}{I_1}\) = 2 + 1 || [2+1 || (2+1)]
z₁₁ = 2 + 1 || (2 + \(\frac{3}{4}\)) = 2 + \(\frac{1×\frac{11}{4}}{1+\frac{11}{4}} = 2 + \frac{11}{15}\) = 2.733
I₀ = \(\frac{1}{1+3}\) I’₀ = \(\frac{1}{4}\) I’₀
And I’₀ = 1 + \(\frac{11}{4}\) I₁ = \(\frac{4}{15}\) I₁
Or, I₀ = \(\frac{1}{4} × \frac{4}{5} I_1 = \frac{1}{15} I_1\)
Or, V₂ = I₀ = \(\frac{1}{15} I_1\)
z₂₁ = \(\frac{V_2}{I_1} = \frac{1}{15}\) = z₁₂ = 0.0667
z₂₂ = \(\frac{V_2}{I_2}\) = 2+1 || (2+1||3) = z₁₁ = 2.733
∴ [z] = [2.733:0.0667; 0.0667:2.733] Ω.

8. For the circuit given below, the value of z₂₂ parameter is ____________

a) z₂₂ = 4 + j6 Ω
b) z₂₂ = j6 Ω
c) z₂₂ = -j4 Ω
d) z₂₂ = -j6 + 4 Ω
View Answer

Answer: c
Explanation: z₁₂ = j6 = z₂₁
z₁₁ – z₁₂ = 4
Or, z₁₁ = z₁₂ + 4 = 4 + j6 Ω
And z₂₂ – z₁₂ = -j10
Or, z₂₂ = z₁₂ + -j10 = -j4 Ω
∴ [z] = [4+j6:j6; j6:-j4] Ω.

9. For the circuit given below, the value of z₂₂ parameter is ____________

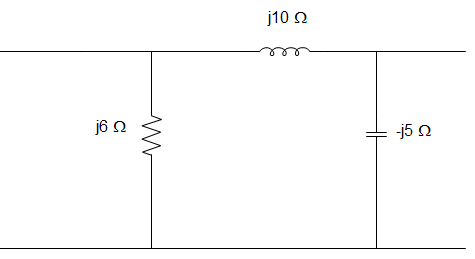
a) z₂₂ = 1.775 + j5.739 Ω
b) z₂₂ = 1.775 – j4.26 Ω
c) z₂₂ = -1.775 – j5.739 Ω
d) z₂₂ = 1.775 + j4.26 Ω
View Answer

Answer: c
Explanation: z₁ = \(\frac{12(j10)}{12+j10-j5} = \frac{j120}{12+j5}\)
z₂ = \(\frac{j60}{12+j5}\)
z₃ = \(\frac{50}{12+j5}\)
z₁₂ = z₂₁ = z₂ = \(\frac{(-j60)(12-j5)}{144+25}\) = -1.775 – j4.26
z₁₁ = z₁ + z₁₂ = \(\frac{(j120)(12-j5)}{144+25}\) + z₁₂ = 1.775 + j4.26
z₂₂ = z₃ + z₂₁ = \(\frac{(50)(12-j5)}{144+25}\) + z₂₁ = 1.7758 – j5.739
∴ [z] = [1.775 + j4.26; -1.775 – j4.26; -1.775 – j4.26; 1.775 – j5.739] Ω.

10. For the circuit given below, the value of z₂₂ parameter is ____________

a) z₂₂ = 20 Ω
b) z₂₂ = 25 Ω
c) z₂₂ = 30 Ω
d) z₂₂ = 24 Ω
View Answer

Answer: c
Explanation: z₁₁ = \(\frac{V_1}{I_1} = \frac{(20+5)I_1}{I_1}\) = 25Ω
V₀ = \(\frac{20}{25}\)V₁ = 20 I₁
-V₀ – 4I₂ + V₂ = 0
Or, V₂ = V₀ + 4I₁ = 20I₁ + 4I₁ = 24 I₁
Or, z₂₁ = \(\frac{V_2}{I_1}\) = 24 Ω
V₂ = (10+20) I₂ = 30 I₂
Or, z₂₂ = \(\frac{V_2}{I_1}\) = 30 Ω
V₁ = 20I₂
Or, z₁₂ = \(\frac{V_1}{I_2}\) = 20 Ω
∴ [z] = [25:20; 24:30] Ω.

11. A capacitor of 220 V, 50 Hz is needed for AC supply. The peak voltage rating of the capacitor is ____________
a) 220 V
b) 460 V
c) 440 V
d) 230 V
View Answer

Answer: c
Explanation: We know that,
Peak voltage rating = 2 (rms voltage rating)
Given that the RMS voltage rating = 220 V
So, the Peak Voltage Rating = 2 X 220 V
= 440 V.

12. In the circuit given below, the value of the hybrid parameter h₂₁ is _________

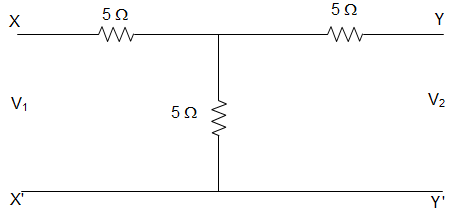
a) 10 Ω
b) 0.5 Ω
c) 5 Ω
d) 2.5 Ω
View Answer

Answer: b
Explanation: Hybrid parameter h₂₁ is given by, h₂₁ = \(\frac{I_2}{I_1}\), when V₂ = 0.
Therefore short circuiting the terminal Y-Y’, and applying Kirchhoff’s law, we get,
-5 I₂ – (I₂ – I₁)5 = 0
Or, -I₂ = I₂ – I₁
Or, -2I₂ = -I₁
∴ \(\frac{I_2}{I_1} = \frac{1}{2}\)
Hence h₂₁ = 0.5 Ω.

13. If a two port network is passive, then we have, with the usual notation, the relationship as _________
a) h₂₁ = h₁₂
b) h₁₂ = -h₂₁
c) h₁₁ = h₂₂
d) h₁₁ h₂₂ – h₁₂ h₂₂ = 1
View Answer

Answer: d
Explanation: We know that, I₁ = y₁₁ V₁ + y₁₂ V₂ ……… (1)
I₂ = y₂₁ V₁ + y₂₂ V₂ ………. (2)
And, V₁ = h₁₁ I₁ + h₁₂ V₂ ………. (3)
I₂ = h₂₁ I₁ + h₂₂ V₂ ……….. (4)
Now, (3) and (4) can be rewritten as,
I₁ = \(\frac{V_1}{h_{11}} – \frac{h_{12} V_2}{h_{11}}\) ………. (5)
And I₂ = \(\frac{h_21 V_1}{h_11} + \left(- \frac{h_{21} h_{12}}{h_{11}} + h_{22}\right) V_2\) ………. (6)
Therefore using the above 6 equations in representing the hybrid parameters in terms of the Y parameters and applying ∆Y = 0, we get,
h₁₁ h₂₂ – h₁₂ h₂₂ = 1 [hence proved].

14. In two-port networks the parameter h₂₂ is called _________
a) Short circuit input impedance
b) Short circuit current gain
c) Open circuit reverse voltage gain
d) Open circuit output admittance
View Answer

Answer: d
Explanation: We know that, h₂₂ = \(\frac{I_2}{V_2}\), when I₁ = 0.
Since the current in the first loop is 0 when the ratio of the current and voltage in second loop is measured, therefore the parameter h₁₂ is called as Open circuit output admittance.

15. The short-circuit admittance matrix of a two port network is as follows.
[0; -0.5; 0.5; 0] Then the 2 port network is ____________
a) Non-reciprocal and passive
b) Non-reciprocal and active
c) Reciprocal and passive
d) Reciprocal and active
View Answer

Answer: b
Explanation: So, network is non reciprocal because Y₁₂ ≠ Y₂₁ and Y₁₂ are also negative which means either energy storing or providing device is available. So the network is active.
Therefore the network is Non- reciprocal and active.

Sanfoundry Global Education & Learning Series – Network Theory.

To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Network Theory Questions and Answers – Series-Parallel Interconnection of Two Port Network

» Next - Network Theory Questions and Answers – Advanced Problems on Two Port Network – 2

Related Posts:

Check Electronics & Communication Engineering Books
Apply for Electronics & Communication Engineering Internship
Practice Electrical Engineering MCQs
Apply for Electrical Engineering Internship
Check Network Theory Books

Recommended Articles: