This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Advanced Problems on Superposition Theorem”.
1. The Superposition Theorem is not applicable for _________
a) Power calculation
b) Voltage calculation
c) Current Calculation
d) Both Voltage and Current calculation
View Answer
Explanation: The Superposition Theorem is not applicable for Power calculation because for power, the calculations involve either the product of voltage and current or the square of current or the square of the voltage thus making them non-linear operations. Hence they cannot be calculated using Superposition Theorem.
2. The current I in the circuit given below is ________
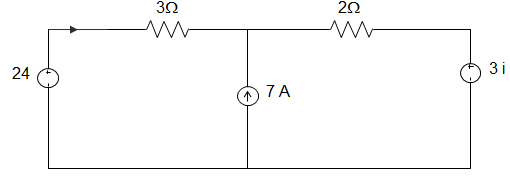
a) \(\frac{1}{4}\) A
b) \(\frac{5}{4}\) A
c) \(\frac{3}{4}\) A
d) \(\frac{1}{2}\) A
View Answer
Explanation: Using Superposition Theorem, we can write
I = \(\frac{24}{3+2} – \frac{72}{3+2} – \frac{3I}{3+2} \)
Or, I = 2 – \(\frac{3I}{3+2}\)
Or, I = 2 – \(\frac{3I}{5}\)
∴ I = \(\frac{5}{4}\) A.
3. The value of the voltage V2 at the node in the circuit given below is __________
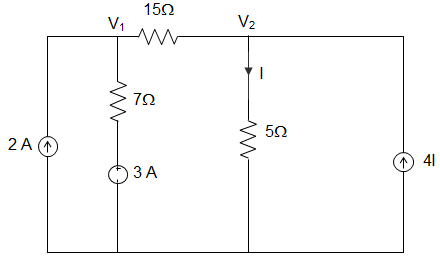
a) 2.745 V
b) 1.393 V
c) -1.393 V
d) -2.745 V
View Answer
Explanation: The datum node is the lower branch.
By superposition, the current i is given by, i = 2 \(\frac{7}{15+5+7} + \frac{3}{15+5+7} + 4I \frac{7+15}{15+5+7}\)
Or, I = \(\frac{17}{27} + \frac{88}{27I}\)
∴ The solution for i yields, I = \(\frac{\frac{17}{27}}{1 – \frac{88}{27}} = -\frac{17}{61}\) A
∴ V2 = 5I = -1.393 V.
4. The value of the voltage V1 at the node in the circuit given below is __________

a) 11.148 V
b) 10.989 V
c) 20.151 V
d) 25.148 V
View Answer
Explanation: The datum node is the lower branch.
By superposition, the current i is given by, i = 2 \(\frac{7}{15+5+7} + \frac{3}{15+5+7} + 4I \frac{7+15}{15+5+7}\)
Or, I = \(\frac{17}{27} + \frac{88}{27I}\)
∴ The solution for i yields, I = \(\frac{\frac{17}{27}}{1 – \frac{88}{27}} = -\frac{17}{61}\) A
∴ V1 = V2 – (4I – i) 15 = 11.148 V.
5. The value of the current I in the circuit given below, is ___________
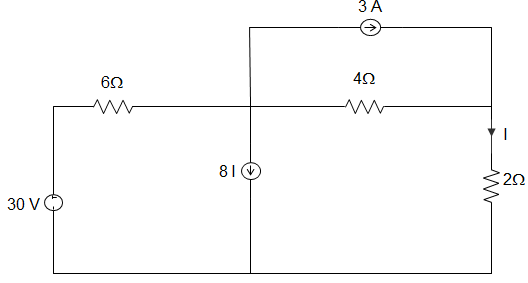
a) 0.7 A
b) 0.5 A
c) 1 A
d) 3.5 A
View Answer
Explanation: Using Superposition theorem, we can write,
I = \(\frac{30}{6+4+2} + 3\frac{4}{6+4+2} – 8i\frac{6}{6+4+2}\)
Or, I = \(\frac{42}{12}\) – 4I
Or, I = \(\frac{\frac{42}{12}}{1+4}\) = 0.7 A.
6. In superposition theorem when we consider one voltage source, all the other voltage sources are ___________
a) Shorted
b) Removed
c) Undisturbed
d) Opened
View Answer
Explanation: To determine the contribution of each individual source in case of Superposition Theorem, we short circuit all the other voltage sources (which are independent) and open circuit all the independent current sources (which are independent).
7. In the figure given below, the value of Resistance R by Superposition Theorem is ___________
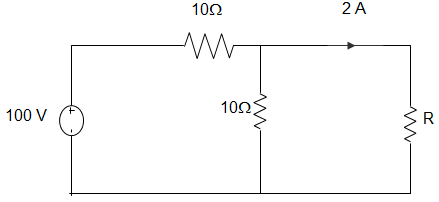
a) 10
b) 20
c) 30
d) 40
View Answer
Explanation: Using Superposition theorem, we get,
\(\frac{V_P-100}{10} + \frac{V_P}{10}\) + 2 = 0
Or, 2VP – 100 +20= 0
∴ VP = 80/2 = 40V
∴ R = 20Ω.
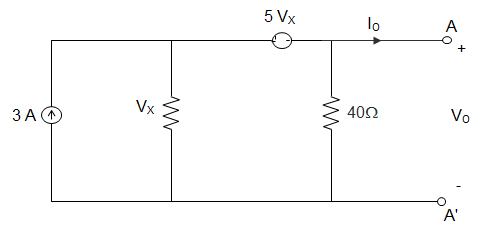
8. In the circuit given below, the value of voltage VX using Superposition Theorem is _________
a) 5(IO – 3)
b) 2.5(IO – 3)
c) 4.5(3 – IO)
d) 2.5(3 – IO)
View Answer
Explanation: Using Superposition Theorem the voltage VX is given as,
VX = (3-IO) (2||40) + 5VX \(\frac{2}{40+2}\)
Or, VX = \(\frac{80}{42}(3 – I_O) + \frac{10}{42}V_X\)
Or, VX = \(\frac{\frac{80}{42}}{1-\frac{10}{42}}(3 – I_O)\) = 2.5(3 – IO).
9. In the circuit given below, the value of voltage VO using Superposition Theorem is _________

a) −30 – 10IO
b) 30 + 10IO
c) −30 + 10IO
d) +30 – 10IO
View Answer
Explanation: Using Superposition Theorem the voltage VX is given as,
VX = (3-IO) (2||40) + 5VX \(\frac{2}{40+2}\)
Or, VX = \(\frac{80}{42}(3 – I_O) + \frac{10}{42}\)VX
Or, VX = \(\frac{\frac{80}{42}}{1-\frac{10}{42}}\)(3 – IO) = 2.5(3 – IO)
∴ VO = VX – 5VX = −30 + 10IO.
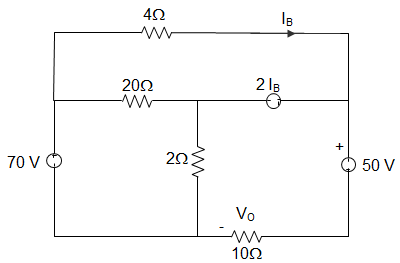
10. The value of the voltage VO in the circuit given below is __________
a) 20 V
b) 30 V
c) 40 V
d) 50 V
View Answer
Explanation: Using Superposition Theorem, the current IB is given by,
IB = \(\frac{70}{4||20+2||10} × \frac{20}{4+20} + \frac{50}{10+4||20||2} × \frac{20||2}{4+20||2} – \frac{2I_B}{20||2+4||10} × \frac{10}{4+10}\)
Or, IB = \(\frac{35}{3} + \frac{25}{18} – \frac{11}{36}\) IB
Now, Solving for IB, we get, IB = \(\frac{\frac{35}{3}+\frac{25}{18}}{1+\frac{11}{36}}\) = 10 A
Now, VO = 70 − 4ib
∴ VO = 30 V.
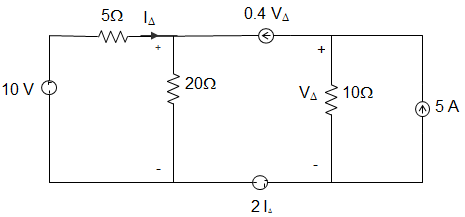
11. The value of voltage VO in the circuit given below is _____________
a) 24 V
b) 48 V
c) 12 V
d) 4 V
View Answer
Explanation: Using Superposition Theorem, we get,
V∆ = −0.4V∆ × 10 + 5 × 10
Solving for V∆, we get, V∆ = \(\frac{5 × 10}{1+0.4×10}\) = 10 V
Again by using Superposition Theorem, we get, I∆ = \(\frac{10}{5+20} – 0.4V_∆ \frac{20}{5+20}\)
Or, I∆ = \(\frac{10}{25} – 0.4V_∆ \frac{20}{25} = -\frac{70}{25}\) A
Thus, VO is given by, VO = 10 − 5I∆
∴ VO = 24 V.
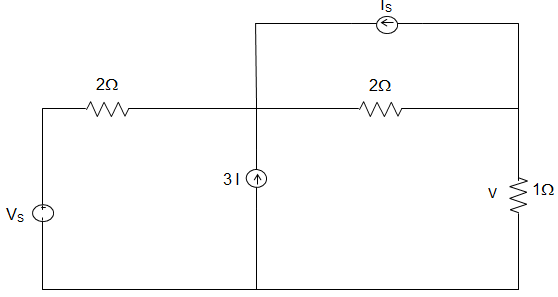
12. In the circuit given below, the value of V in terms of VS and IS using Superposition Theorem is ___________
a) V = \(\frac{2}{7} I_S – \frac{4}{7} V_S\)
b) V = \(\frac{2}{7} V_S + \frac{4}{7} I_S\)
c) V = \(\frac{2}{7} V_S – \frac{4}{7} I_S\)
d) V = \(\frac{2}{7} I_S – \frac{4}{7} V_S\)
View Answer
Explanation: By superposition, the current I is given by I = \(\frac{V_S}{5} − \frac{2}{5} × I_S − \frac{3}{5} × 3i\)
This can be solved for I to obtain, I = \(\frac{V_S}{14} – \frac{I_S}{7}\)
Now, by Superposition Theorem, V = \(\frac{V_S}{5} − \frac{2}{5} × I_S − \frac{3}{5} × 3i\)
Or, V = \(\frac{V_S}{5} − \frac{2}{5} × I_S − \frac{3}{5} × 3(\frac{V_S}{14} – \frac{I_S}{7})\)
∴ V = \(\frac{2}{7} V_S – \frac{4}{7} I_S\).
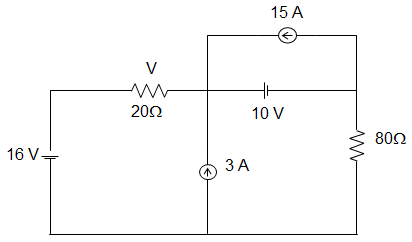
13. In the circuit given below, the value of VX due to the 10 V source is ____________
a) 1 V
b) 2 V
c) 3 V
d) 4 V
View Answer
Explanation: Due to the effect of the 10 V source, we short the 16 V source and open the 3A and 15 A sources. From the resulting circuit, we can calculate the value of V.
∴ V = \(\frac{10 ×20}{80+20}\) = 2 V.
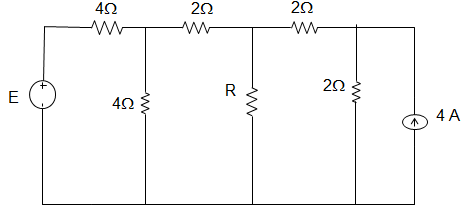
14. In the following circuit, when R = 0 Ω, the current IR equals to 10 A. The maximum power will be?
a) 50 W
b) 100 W
c) 200 W
d) 400 W
View Answer
Explanation: Using Superposition Theorem, we get, I = 10 A and R = 2 Ω
∴ Pmax = (\(\frac{10}{2}\))2 × 2
= 5 × 5 × 2 = 50 W.
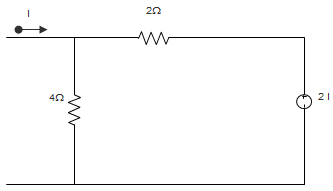
15. The circuit shown in figure has a load equivalent to _________
a) \(\frac{4}{3}\) Ω
b) \(\frac{8}{3}\) Ω
c) 4 Ω
d) 2 Ω
View Answer
Explanation: Using Superposition Theorem, in the given circuit, \(\frac{V}{4} + \frac{V-2I}{2}\) = I
Or, \(\frac{3V-4I}{4}\) = I
Or, 3V = 8I
∴ \(\frac{V}{I} = \frac{8}{3}\) Ω.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
