This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Series Circuits”.
1. If we apply a sinusoidal input to RL circuit, the current in the circuit is __________ and the voltage across the elements is _______________
a) square, square
b) square, sinusoid
c) sinusoid, square
d) sinusoid, sinusoid
View Answer
Explanation: If we apply a sinusoidal input to RL circuit, the current in the circuit is square and the voltage across the elements is sinusoid. In the analysis of the RL series circuit, we can find the impedance, current, phase angle and voltage drops.
2. The circuit shown below consists of a 1kΩ resistor connected in series with a 50mH coil, a 10V rms, 10 KHz signal is applied. Find impedance Z in rectangular form.
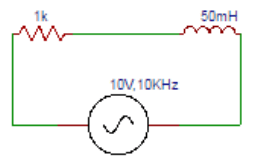
a) (1000+j0.05) Ω
b) (100+j0.5) Ω
c) (1000+j3140) Ω
d) (100+j3140) Ω
View Answer
Explanation: Inductive Reactance XL = ωL = 2πfL = (6.28)(104)(50×10-3) = 3140Ω. In rectangular form, total impedance Z = (1000+j3140) Ω.
3. Find the current I (mA) in the circuit shown below.

a) 3.03
b) 30.3
c) 303
d) 0.303
View Answer
Explanation: Total impedance Z = (1000+j3140) Ω. Magnitude = 3295.4Ω
Current I=Vs/Z = 10/3295.4=3.03mA.
4. Find the phase angle θ in the circuit shown below.

a) 62.33⁰
b) 72.33⁰
c) 82.33⁰
d) 92.33⁰
View Answer
Explanation: Phase angle θ = tan-1(XL/R). The values of XL, R are XL = 3140Ω and R = 1000Ω. On substituting the values in the equation, phase angle θ =tan-1(3140/1000)=72.33⁰.
5. In the circuit shown below, find the voltage across resistance.

a) 0.303
b) 303
c) 3.03
d) 30.3
View Answer
Explanation: Voltage across resistance = IR. The values of I = 3.03 mA and R = 10000Ω. On substituting the values in the equation, the voltage across resistance = 3.03 x 10-3×1000 = 3.03V.
6. In the circuit shown below, find voltage across inductive reactance.

a) 9.5
b) 10
c) 9
d) 10.5
View Answer
Explanation: Voltage across inductor = IXL. The values of I = 3.03 mA and XL = 10000Ω. On substituting the values in the equation, the voltage across inductor = 3.03×10-3×1000 = 9.51V.
7. Determine the source voltage if voltage across resistance is 70V and the voltage across inductor is 20V as shown in the figure.
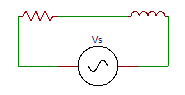
a) 71
b) 72
c) 73
d) 74
View Answer
Explanation: If voltage across resistance is 70V and the voltage across inductor is 20V, source voltage Vs=√(702+202) = 72.8≅73V.
8. Find the phase angle in the circuit shown below.

a) 15
b) 16
c) 17
d) 18
View Answer
Explanation: The phase angle is the angle between the source voltage and the current. Phase angle θ=tan-1(VL/VR). The values of VL = 20V and VR = 70V. On substituting the values in the equation, phase angle in the circuit = tan-1(20/70)=15.94o≅ 16o.
9. An AC voltage source supplies a 500Hz, 10V rms signal to a 2kΩ resistor in series with a 0.1µF capacitor as shown in the following figure. Find the total impedance.
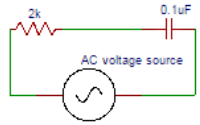
a) 3750.6Ω
b) 3760.6Ω
c) 3780.6Ω
d) 3790.6Ω
View Answer
Explanation: The capacitive reactance XC = 1/2πfC = 1/(6.28×500×0.1×10-6))=3184.7Ω. In rectangular form, X = (2000-j3184.7)Ω. Magnitude = 3760.6Ω.
10. Determine the phase angle in the circuit shown below.

a) 58
b) 68
c) -58
d) -68
View Answer
Explanation: The phase angle in the circuit is phase angle θ = tan-1(-XC/R) =tan-1((-3184.7)/2000)=-57.87o≅-58o.
11. Find the current I (mA) in the circuit shown below.

a) 2.66
b) 3.66
c) 4.66
d) 5.66
View Answer
Explanation: The term current is the ratio of voltage to the impedance. The current I (mA) in the circuit is current I = VS / Z = 10/3760.6 = 2.66mA
12. Find the voltage across the capacitor in the circuit shown below.

a) 7
b) 7.5
c) 8
d) 8.5
View Answer
Explanation: The voltage across the capacitor in the circuit is capacitor voltage = 2.66×10-3×3184.7 =8.47V.
13. Determine the voltage across the resistor in the circuit shown below.

a) 3
b) 4
c) 5
d) 6
View Answer
Explanation: The voltage across the resistor in the circuit resistive voltage = 2.66×10-3×3184.7 = 5.32V.
14. In the circuit shown below determine the total impedance.
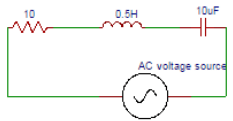
a) 161
b) 162
c) 163
d) 164
View Answer
Explanation: Reactance across capacitor = 1/(6.28×50×10×10-6) = 318.5Ω.
Reactance across inductor = 6.28×0.5×50=157Ω. In rectangular form, Z = (10+j157-j318.5) Ω = (10-j161.5)Ω. Magnitude=161.8Ω.
15. Find the current in the circuit shown below.

a) 0.1
b) 0.2
c) 0.3
d) 0.4
View Answer
Explanation: The term current is the ratio of voltage to the impedance. The current in the circuit is current I=VS/Z = 50/161.8 = 0.3A.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
