This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Advanced Problems on Filters – 1”.
1. In the circuit given below, C= C1 = C2. The gain of the multiple-feedback band-pass filter is ___________
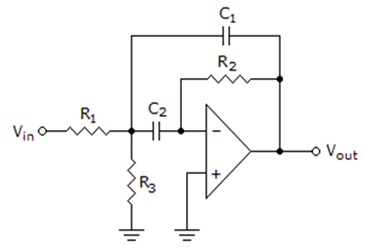
a) A0 = \(\frac{R_2}{R_1}\)
b) A0 = \(\frac{R_1}{R_2}\)
c) A0 = \(\frac{R_2}{2R_1}\)
d) A0 = \(\frac{R_1}{2R_2}\)
View Answer
Explanation: The total output C = CINPUT + COUTPUT that is the gain capacitor.
∴ The total Resistance is equal to the Resistance input and Resistance output.
Again, the total resistance gain = \(\frac{R_1 R_2}{R_1 + R_2}\)
Hence, the gain = A0 = \(\frac{R_2}{2R_1}\).
2. Two network functions are given below.
H1 = \(\frac{1}{s^2 + \sqrt{2}s+1}\), H2 = \(\frac{1}{s^3+2s^2+2s+1}\)
The frequency response indicates that the filter is ___________
a) Low-pass
b) Band-pass
c) High-pass
d) Band reject
View Answer
Explanation: | H1 |2 = \(\frac{1}{[(jω)^2 + \sqrt{2} jω+1] [(jω)^2 + \sqrt{2} jω+1]}\)
Similarly, | H2 |2 = \(\frac{1}{1 + ω^6}\)
Therefore at ω = 0, 1 and ∞, we have | H |2 = 1, \(\frac{1}{2}\) and 0 respectively.
Hence, the filter is a Low-pass filter.
3. A particular band-pass function has a network function as H(s) = \(\frac{3s}{s^2+4s+3}\) then, its quality factor Q is ___________
a) \(\frac{3}{4}\)
b) \(\frac{2}{\sqrt{3}}\)
c) \(\frac{\sqrt{3}}{2}\)
d) \(\frac{\sqrt{3}}{4}\)
View Answer
Explanation: H(s) = \(\frac{Ks}{s^2+as+b}\)
Then, quality factor is given as \(\frac{\sqrt{b}}{a}\)
Here, b = 3, a = 4
∴ Q = \(\frac{\sqrt{3}}{4}\).
4. In which of the filter circuits given below, will the bandwidth be equal to the critical frequency?
a) Low-pass
b) High-pass
c) Band-pass
d) Band-stop
View Answer
Explanation: Bandwidth can be calculated by considering,
Largest positive value – Smallest Positive Value
Here, in case of the Low-pass filter only, the largest positive value will of course be the critical frequency, beyond which frequencies have to be blocked. Hence, the bandwidth in a Low-pass filter equals the critical frequency.
5. In the circuit given below, the Roll-off of the filter is _______________
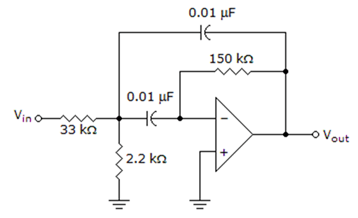
a) 20 dB/decade
b) 40 dB/decade
c) 60 dB/decade
d) 80 dB/decade
View Answer
Explanation: The given filter is a first order Band Pass Filter.
Also, the Roll-off of the filter is depends upon the order of the filter.
For a first order it is 20dB/decade, for second order it is 40dB/decade, and so on.
Therefore, the Roll-off of the filter = 20 dB/decade.
6. The circuit given below, represents which filter?

a) Low-pass
b) High-pass
c) Band-pass
d) Band-stop
View Answer
Explanation: From the given circuit, we can infer that Roll off of the Filter circuit is 80dB/decade. This Roll-off value is obtained as second order high pass filter followed by another 2nd order HPF results in an HPF.
Therefore the circuit represents a High-pass Filter.
7. A Low-pass filter circuit has a cut-off frequency of 1.23 kHz. The bandwidth of the filter is ______________
a) 2.46 kHz
b) 1.23 kHz
c) 0.615 kHz
d) 3.69 kHz
View Answer
Explanation: The bandwidth is defined as the highest cut-off frequency to the lowest cut-off frequency. Here the lowest cut-off frequency is Zero.
For a Low-pass filter therefore, Cut-off Frequency = Bandwidth of the filter
∴ Bandwidth = 1.23 kHz.
8. For the circuit given below, the Roll-off value of the filter is _____________

a) 20 dB/decade
b) 40 dB/decade
c) 60 dB/decade
d) 80 dB/decade
View Answer
Explanation: The given filter is a first order Band Pass Filter. Also, the Roll-off of the filter is depends upon the order of the filter. For a first order it is 20dB/decade, for second order it is 40dB/decade, and so on.
Therefore, the Roll-off of the filter = 20 dB/decade.
Roll of first order low pass Butterworth filter is 20dB/decade.
Now here two stages of second order Low-pass Butterworth filter are cascaded
∴ Roll-off = 20*4 = 80 dB/decade.
9. For providing a Roll-off greater than 20dB/decade/pole, filters with which characteristics are useful?
a) Butterworth
b) Chebyshev
c) Bessel
d) Butterworth & Bessel
View Answer
Explanation: Roll off is a term commonly refers to the steepness of the transmission function wrt to the frequency.
For a Chebyshev filter, the Roll-off value greater than 20. This characteristic feature is useful when a rapid roll-off is required because it provides a Roll-off rate of more than 20.
On the other hand, both Butterworth and Bessel have the Roll-off rate less than or equal to 20 dB/decade/pole.
10. In a moving iron meter, the deflection torque is proportional to?
a) Square of the current through the coil
b) Current through the coil
c) Sine of measurand
d) The Square root of the measurand
View Answer
Explanation: We know that Td = \(\frac{1}{2} I^2 \frac{dl}{dθ}\)
Hence, the deflection torque is proportional to the square of the current through the coil.
11. The filter which passes all frequencies above fc by attenuating significantly, all frequencies below fc is _______________
a) Low-pass
b) High-pass
c) Band-pass
d) Band-stop
View Answer
Explanation: A high-pass filter is one which passes all frequencies above fc by attenuating significantly, all frequencies below fc.
12. The circuit given below represents which type of filter circuit?
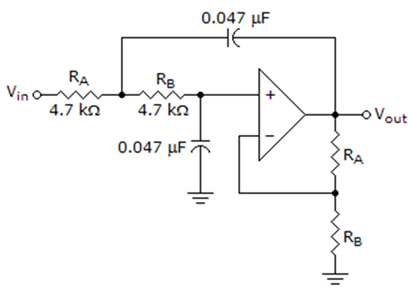
a) Low-pass Filter
b) High-pass Filter
c) Band-pass Filter
d) Band-stop Filter
View Answer
Explanation: The given circuit is a first order Band Pass Filter. Also, the Roll-off of the filter depends upon the order of the filter. For a first order it is 20dB/decade, for second order it is 40dB/decade, and so on.
13. For the circuit given below, the cut-off frequency of the filter is ________________

a) 3225.8 Hz
b) 7226 Hz
c) 3225.8 kHz
d) 7226 kHz
View Answer
Explanation: We know that, F = \(\frac{1}{2π×(R_1×R_2)×(C_1×C_2)}\)
Where, R1 = 4700 Ω, R2 = 4700 Ω, C1 = 0.047 × 10-6 F, C2 = 0.047×10-6 F
∴ F = \(\frac{1}{2π×(4700×4700)×(C_1×C_2)}\)
= \(\frac{1}{2π×48796.81×10^{-12}}\)
= \(\frac{10^6}{2π×0.04879681}\)
= \(\frac{10^6}{0.30654156042}\) = 3225.8 kHz.
14. The circuit given below represents which type of filter circuit?
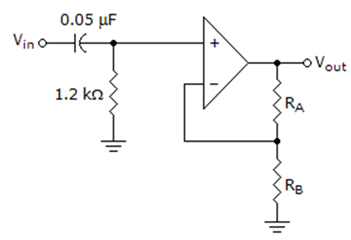
a) Low-pass Filter
b) High-pass Filter
c) Band-pass Filter
d) Band-stop Filter
View Answer
Explanation: We know that the position of Resistance (R) and Capacitance (C) determines whether it is Low-pass Filter or High-Pass Filter. If R is connected directly to source and the capacitor connected in parallel to it, then it is a Low-pass Filter and if the position of R and C are inter change then high pass filter is formed.
Here since R and C are in series and also R is not connected directly to the power source, hence the filter is a High-pass Filter.
15. For the circuit given below, the cut-off frequency of the filter is ________________

a) 5283 kHz
b) 5283 Hz
c) 2653.1 kHz
d) 2653.1 Hz
View Answer
Explanation: We know that, F = \(\frac{1}{2π×R×C}\)
Where, R = 1200 Ω, C1 = 0.05×10-6 F
∴ F = \(\frac{1}{2π×1200×C}\)
= \(\frac{1}{2π×60×10^{-6}}\)
= \(\frac{10^6}{2π×60}\) = 2653.1 Hz.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Electrical Engineering MCQs
- Apply for Electrical Engineering Internship
- Check Electrical Engineering Books
- Apply for Electronics & Communication Engineering Internship
- Practice Electronics & Communication Engineering MCQs
