This set of Network Theory Objective Questions & Answers focuses on “Advanced Problems on Application of Laplace Transform – 2”.
1. A capacitor of 110 V, 50 Hz is needed for AC supply. The peak voltage of the capacitor should be ____________
a) 110 V
b) 460 V
c) 220 V
d) 230 V
View Answer
Explanation: We know that,
Peak voltage rating = 2 (rms voltage rating).
Given that, rms voltage rating = 110 V
So, Peak voltage rating = 110 X 2 V
= 220 V.
2. Given I (t) = 10[1 + sin (- t)]. The RMS value of I(t) is ____________
a) 10
b) 5
c) \(\sqrt{150}\)
d) 105
View Answer
Explanation: Given that, I (t) = 10[1 + sin (- t)]
Now, RMS value = \(\sqrt{10^2 + \frac{10^2}{\sqrt{2}}}\)
= \(\sqrt{100+50}\)
= \(\sqrt{150}\).
3. A two branch parallel circuit has a 50 Ω resistance and 10 H inductance in one branch and a 1 μF capacitor in the second branch. It is fed from 220 V ac supply, at resonance, the input impedance of the circuit is _____________
a) 447.2 Ω
b) 500 Ω
c) 235.48 Ω
d) 325.64 Ω
View Answer
Explanation: We know that,
For a parallel resonance circuit impedance = \([\frac{L}{RC}]^{0.5}\)
Given, R = 50 Ω, L = 10 H and C = 1 μF
= \([\frac{10}{50*1}]^{0.5}\)
So, impedance = 447.2 Ω.
4. The impedance matrices of two, two-port network are given by [3 2; 2 3] and [15 5; 5 25]. The impedance matrix of the resulting two-port network when the two networks are connected in series is ____________
a) [3 5; 2 25]
b) [18 7; 7 28]
c) [15 2; 5 3]
d) Indeterminate
View Answer
Explanation: Given that two impedance matrices are [3 2; 2 3] and [15 5; 5 25]. Here, the resulting impedance is the sum of the two given impedances.
So resulting impedance = [18 7; 7 28].
5. The electrical energy required to heat a bucket of water to a certain temperature is 10 kWh. If heat losses, are 10%, the energy input is ____________
a) 2.67 kWh
b) 3 kWh
c) 2.5 kWh
d) 3.5 kWh
View Answer
Explanation: Given that, 10% of input is lost.
So, 0.90 Input = 10
Or, Input = \(\frac{10}{0.9}\) = 11.11 kWh.
6. The current rating of a cable depends on ___________
a) Length of the cable
b) Diameter of the cable
c) Both length and diameter of the cable
d) Neither length nor diameter of the cable
View Answer
Explanation: We know that Current rating depends only on the area of cross-section. Since the area of cross section is a function of radius, which in turn is a function of diameter, so the current rating depends only on the Diameter of the cable.
7. In an AC circuit, the maximum and minimum values of power factor can be ___________
a) 2 and 0
b) 1 and 0
c) 0 and -1
d) 1 and -1
View Answer
Explanation: We know that, power factor is maximum and equal to 1 for a purely resistive load. Power factor is minimum and equal to zero for a purely reactive load.
Hence, in an AC circuit, the maximum and minimum values of power factor are 1 and 0 respectively.
8. In the circuit given below, the series circuit shown in figure, for series resonance, the value of the coupling coefficient, K will be?
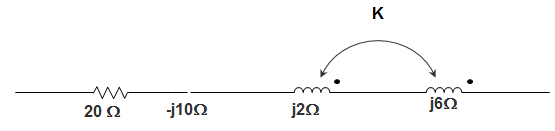
a) 0.25
b) 0.5
c) 0.1
d) 1
View Answer
Explanation: Mutual inductance wm = ω k \(\sqrt{L_1 L_2}\)
Or, m = k.2.8 j2
= 4k.j
At resonance, Z = 20 – j10 + j2 + j6 + 2.4kj – 2j + 8kj = 0
Or, -2 = -8k
Or, k = \(\frac{1}{4}\) = 0.25.
9. In an RC series circuit R = 100 Ω and XC = 10 Ω. Which of the following is possible?
a) The current and voltage are in phase
b) The current leads the voltage by about 6°
c) The current leads the voltage by about 84°
d) The current lags the voltage by about 6°
View Answer
Explanation: In RC circuit the current leads the voltage.
Or, θ = tan-1 \(\frac{10}{100}\)
This is nearly equal to 6°
Hence, the current lags the voltage by about 6°.
10. The impedance of an RC series circuit is 12 Ω at f = 50 Hz. At f = 200 Hz, the impedance will be?
a) More than 12
b) Less than 3
c) More than 3 Ω but less than 12 Ω
d) More than 12 Ω but less than 24 Ω
View Answer
Explanation: We know that the impedance Z, is given by
Z = R2 + \(X_C^2\)
When f is made four times, XC becomes one-fourth but R remains the same.
So, the impedance is more than 3 Ω but less than 12 Ω.
11. A 3 phase balanced supply feeds a 3-phase unbalanced load. Power supplied to the load can be measured by ___________
a) 2 Wattmeter and 1 Wattmeter
b) 2 Wattmeter and 3 Wattmeter
c) 2 Wattmeter and 2 Wattmeter
d) Only 3 Wattmeter
View Answer
Explanation: We know that, a minimum of 2 wattmeters is required to measure a 3-phase power. Also, power can be measured by using only one wattmeter in each phase. Hence, power supplied to the load can be measured by 2 Wattmeter and 3 Wattmeter methods.
12. A series RC circuit has R = 15 Ω and C = 1 μF. The current in the circuit is 5 sin 10t. The applied voltage is _____________
a) 218200 cos (10t – 89.99°)
b) 218200 sin (10t – 89.99°)
c) 218200 sin (10t)
d) 218200 cos (10t)
View Answer
Explanation: Given that, R = 15Ω, XC = \(\frac{1}{ωC}\)
= \(\frac{10^6}{10 X 1}\) = 105 Ω
Now, θ = tan-1 \(\frac{X_C}{R}\) = 89.99°
We know that, impedance Z is given by,
Z = \(\sqrt{R^2 + X_C^2}\) = 102 kΩ.
Hence, V = 100000(2.182).sin(10 t – 89.99°)
Or, V = 218200 sin (10t – 89.99°).
13. A capacitor stores 0.15C at 5 V. Its capacitance is ____________
a) 0.75 F
b) 0.75 μF
c) 0.03 F
d) 0.03 μF
View Answer
Explanation: We know that, Q = CV
Given, V = 5 V, Q = 0.15 C
Hence, 0.15 = C(5)
Or, C = 0.03 F.
14. For a transmission line, open circuit and short circuit impedances are 10 Ω and 20 Ω. Then characteristic impedance is ____________
a) 100 Ω
b) 50 Ω
c) 25 Ω
d) 200 Ω
View Answer
Explanation: We know that, the characteristic impedance Z0 is given by,
Z0 = Zoc Zsc
Given that, open circuit impedance, Zoc = 10 Ω and short circuit impedance, Zsc = 20 Ω.
So, Z0 = (10.20) Ω
= 200 Ω.
15. A circuit excited by voltage V has a resistance R which is in series with an inductor and a capacitor connected in parallel. The voltage across the resistor at the resonant frequency is ___________
a) 0
b) \(\frac{V}{2}\)
c) \(\frac{V}{3}\)
d) V
View Answer
Explanation: Dynamic resistance of the tank circuit, ZDY = \(\frac{L}{R_LC}\)
But given that RL = 0
So, ZDY = \(\frac{L}{0XC}\) = ∞
Therefore current through the circuit, I = \(\frac{V}{∞}\) = 0
∴ VD = 0.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all objective questions on Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
