This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Advanced Problems on Resonance”.
1. For a series RLC circuit, excited by voltage V = 20 sinωt. The values of R = 2 Ω, L = 1mH and C = 0.4 µF. The resonant frequency of the circuit is ______________
a) 20 krad/s
b) 30 krad/s
c) 40 krad/s
d) 50 krad/s
View Answer
Explanation: We know that the resonant frequency w0 = 1/(LC)0.5
Given R = 2 Ω, L = 1mH and C = 0.4 µF.
So, w0 = \(\frac{1}{\sqrt{10^{-3}×0.4×10^{-6}}}\)
Or, w0 = 50 krad/s.
2. For a series RLC circuit, excited by voltage V = 20 sinωt. The values of R = 2 Ω, L = 1mH and C = 0.4 µF. The quality factor and bandwidth of the circuit is ______________
a) 25, 2
b) 30, 5
c) 40, 10
d) 50, 2
View Answer
Explanation: We know that, the bandwidth is, B = w2 – w1 = 2 krad/s
Also, B = \(\frac{R}{L} = \frac{2}{10^{-3}}\) = 2 krad/s
Also, the quality factor is given by, Q = \(\frac{w_0}{B}\)
Or, Q = \(\frac{w_0}{B} = \frac{50}{2}\) = 25.
3. An ideal transformer is rated as 2400/120 V, 9.6 kVA and has 50 turns on the secondary side. The turns ratio is ____________
a) 0.04
b) 0.05
c) 0.06
d) 0.07
View Answer
Explanation: The given transformer is a step down transformer.
So, V1 = 2400 V
But it is greater than V2 which is equal to 120V
So, the turns ratio, n = \(\frac{V_2}{V_1} = \frac{120}{2400}\) = 0.05.
4. In the circuit shown in the figure, if ω = 40 rad/s, then Zin is _____________
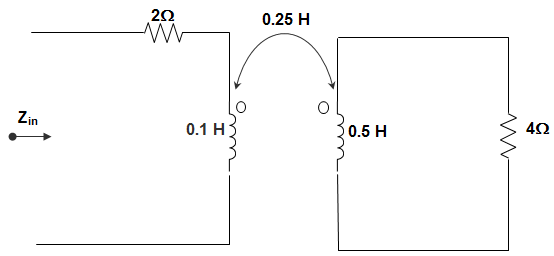
a) 4.77 – j1.15 Ω
b) 2.96 – j0.807 Ω
c) 2.26 – j3.48 Ω
d) 2.26 – j3.48 Ω
View Answer
Explanation: Z = Z11 + \(\frac{ω^2 M^2}{Z_{22}} \)
Or, Z = 2 + j (40) \((\frac{1}{10}) + \frac{40^2 (\frac{1}{4})^2}{4+j(40)\frac{1}{2}}\)
= 2 + j (4) + \(\frac{100}{4+j (20)} \)
= 2 + j (4) + \(\frac{100}{4+j (20)} × \frac{4-j (20)}{4-j (20)}\)
= 2 + j (4) + \(\frac{400-j (2000)}{416}\)
= 2.96 – j0.807 Ω.
5. For the circuit shown in the figure below, the value of R for critical damping will be?
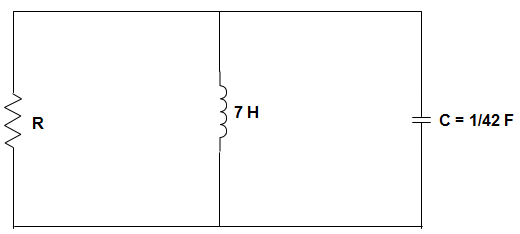
a) 10.5 Ω
b) 8.57 Ω
c) 3.5 Ω
d) 3 Ω
View Answer
Explanation: For a parallel RLC circuit, \(\frac{d^2 V}{dt^2} + \frac{1}{RC} \frac{dV}{dt} + \frac{V}{LC}\) = 0
Solving the 2nd order differential equation, we get, 2rωn = \(\frac{1}{RC}\) and ωn = \(\frac{1}{\sqrt{LC}}\)
As, r=1,
∴ R = \(\frac{1}{2} \sqrt{\frac{L}{C}} \)
= \(\frac{1}{2} \sqrt{\frac{7}{\frac{1}{42}}} = \frac{1}{2}\) × 17.15 = 8.57 Ω.
6. The circuit shown in the figure below will act as an ideal source with respect to terminal A and B when the frequency is ___________
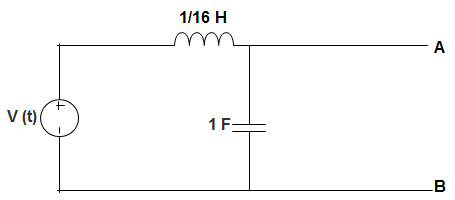
a) Zero
b) 1 rad/s
c) 4 rad/s
d) 16 rad/s
View Answer
Explanation: Z(s) t = \(\frac{(Ls)\frac{1}{Cs}}{Ls + \frac{1}{Cs}} = \frac{Ls}{LCs^2+1} \)
Putting s = jω, we get, Z (jω) = \(\frac{jωL}{1 -LCω^2} \)
For ideal current source, Z (jω) = ∞
Or, 1 – LCω2 = 0
Or, ω = \(\frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{\frac{1}{16}×1}}\) = 4 rad/s.
7. An ideal capacitor is charged to a voltage V and connected at t=0 across an ideal inductor L. If we take ω = \(\frac{1}{\sqrt{LC}}\), the voltage across the capacitor at time t>0 will be?
a) V
b) V cos(ωt)
c) V sin(ωt)
d) Ve-ωt cos(ωt)
View Answer
Explanation: Voltage across the capacitor will discharge through inductor unless the voltage across the capacitor becomes zero. Now, the inductor will start charging the capacitor. Voltage across the capacitor will be decreasing from V and will be periodic. But it will not be decaying with time, since both L and C are ideal.
∴ Voltage across the capacitor at time t>0 is given by V cos (ωt).
8. The RL circuit in the below figure is fed from a constant magnitude, variable frequency sinusoidal voltage source VIN. At 50 Hz, the R and L elements each have a voltage drop Vrms. If the frequency of the source is changed to 25 Hz, the new voltage drop across R is ___________
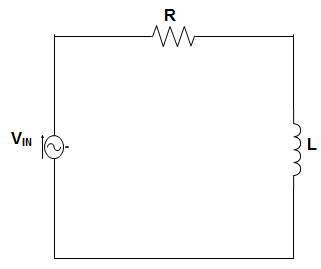
a) \(\sqrt{\frac{5}{8}}\) Vrms
b) \(\sqrt{\frac{2}{3}}\) Vrms
c) \(\sqrt{\frac{8}{5}}\) Vrms
d) \(\sqrt{2}\) Vrms
View Answer
Explanation: At 50 Hz, VR = VL and R = ωL
Also Vrms = \(\frac{V_{in}}{\sqrt{2}} \)
At 25 Hz, Iin = \(\frac{V_{in}}{\sqrt{R^2+\frac{ω^2 L^2}{4}}}\)
= \(\frac{V_{in}}{\sqrt{ω^2 L^2 + \frac{ω^2 L^2}{4}}} = \frac{2V_{in}}{\sqrt{5} ωL}\)
So, Vnew = \(\frac{2V_{in}}{\sqrt{5} ωL} × R = \frac{2V_{in}}{\sqrt{5}}\)
= \(\frac{2\sqrt{2} V_{rms}}{\sqrt{5}} = \sqrt{\frac{8}{5}}\) Vrms.
9. In a series circuit with R = 10Ω and C = 25 μF, at what frequency will the current lead the voltage by 30°?
a) 11.4 kHz
b) 4.5 kHz
c) 1.1 kHz
d) 24.74 kHz
View Answer
Explanation: From the impedance diagram, 10 -jXC = Z∠-30°
∴ – XC = 10 tan (-30°) = -5.77 Ω
∴ XC = 5.77 Ω
Then, XC = \(\frac{1}{2πfC}\) or, f = \(\frac{1}{2πX_C C} \)
= \(\frac{1}{2π×5.77×25×10^{-6}}\)
= \(\frac{10^6}{906.18}\)
= 1103 HZ = 1.1 kHz.
10. The frequency for the given circuit when the circuit is in a state of resonance will be?
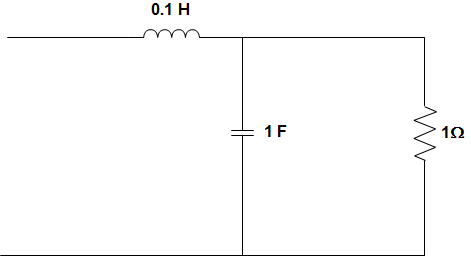
a) 1 rad/s
b) 2 rad/s
c) 3 rad/s
d) 4 rad/s
View Answer
Explanation: Z = jωL + \(\frac{R}{1+jωRC} \)
∴ Z = j0.1ω + \(\frac{1}{1+jω} × \frac{1-jω}{1-jω} \)
= j0.1ω + \(\frac{1-jω}{1+ω^2} = \frac{1}{1+ω^2} + j (0.1ω – \frac{ω}{1 + ω^2}) \)
At resonance, imaginary part must be zero.
0.1 ω – \(\frac{ω}{ 1+ ω^2}\) = 0
Or, 0.1 = \(\frac{1}{1+ω^2}\)
Or, ω2 + 1 = 10
∴ ω2 = 9
Or, ω = 3 rad/s.
11. The time constant for the given circuit under resonance condition will be?
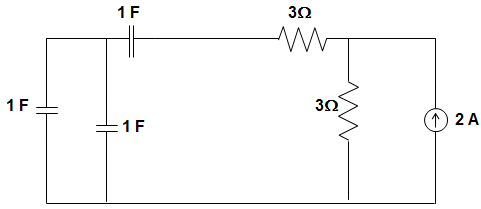
a) \(\frac{1}{9}\) s
b) \(\frac{1}{4}\) s
c) 4 s
d) 9 s
View Answer
Explanation: For finding the time constant, we neglect current source as an open circuit.
Hence, the circuit becomes:
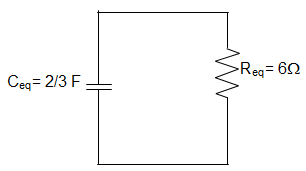
So, from the above circuit, the Time constant = Req Ceq = 6 × \(\frac{2}{3}\) = 4 s.
12. A 50 μF capacitor, when connected in series with a coil having a resistance of 40Ω, resonates at 1000 Hz. The circuit is in resonating condition. The voltage across the capacitor is __________
a) 8.04 V
b) 7.96 V
c) 5.68 V
d) 1.25 V
View Answer
Explanation: At resonance, | I | = \(\frac{V}{Z} = \frac{V}{R} \)
Given that, R = 40Ω and V = 100 V
∴ | I | = \(\frac{100}{40}\) = 2.5 A
Power loss of the coil = I2 R = 2.52 × 40 = 250 W
Also, VC = IXC = 2.5 × \(\frac{1}{2πfC}\) and XC = \(\frac{1}{2πfC}\)
= 2.5 × \(\frac{1}{2π×1000×50×10^{-6}}\)
= 2.5 × \(\frac{100}{31.41}\) = 5.68 V.
13. An ideal transformer is rated as 2400/120 V, 9.6 kVA and has 50 turns on the secondary side. The number of turns on the primary side is ____________
a) 1000
b) 2000
c) 3000
d) 4000
View Answer
Explanation: Turns ratio, n = \(\frac{N_2}{N_1}\)
Now, the turns ratio, n = \(\frac{V_2}{V_1} = \frac{120}{2400}\) = 0.05
Also, n = \(\frac{50}{N_1}\)
So, N1 = \(\frac{50}{0.05}\) = 1000 turns.
14. A 50 μF capacitor, when connected in series with a coil having resistance of 40Ω, resonates at 1000 Hz. The circuit current if the applied voltage is 100 V for the resonant circuit is ___________
a) 2.5 A
b) 3.5 A
c) 4.5 A
d) 0.5 A
View Answer
Explanation: We know that the magnitude of current |I| for a resonating circuit is given by,
| I | = \(\frac{V}{Z} = \frac{V}{R} \)
Given that, R = 40Ω and V = 100 V
∴ | I | = \(\frac{100}{40}\) = 2.5 A.
15. A 50 μF capacitor, when connected in series with a coil having resistance of 40Ω, resonates at 1000 Hz. The circuit is in resonating condition. The voltage across the coil is __________
a) 100.31 V
b) 200.31 V
c) 300.31 V
d) 400.31 V
View Answer
Explanation: At resonance, | I | = \(\frac{V}{Z} = \frac{V}{R} \)
Given that, R = 40Ω and V = 100 V
∴ | I | = \(\frac{100}{40}\) = 2.5 A
XL = ωL = 2π × 1000 × 0.5 × 10-3
= 2π × 0.5 = 3.14 Ω
∴ VCOIL = I Z (At resonance)
= 2.5 \(\sqrt{40^2 + 3.14^2}\)
= 2.5 × 40.122 = 100.31 V.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Electrical Engineering MCQs
- Check Network Theory Books
- Practice Electronics & Communication Engineering MCQs
- Check Electrical Engineering Books
- Apply for Electrical Engineering Internship
