This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Problems Involving Dot Conventions”.
1. The current through an electrical conductor is 1A when the temperature of the conductor 0°C and 0.7 A when the temperature is 100°C. The current when the temperature of the conductor is 1200°C is ___________
a) 0.08 A
b) 0.16 A
c) 0.32 A
d) 0.64 A
View Answer
Explanation: \(\frac{1}{0.7} = \frac{R_O (1+αt)}{R_O}\)
= 1 + α100
∴α = 0.0043 per °C
Current at 1200 °C is given by, \(\frac{1}{I} = \frac{R_O (1+α1200)}{R_O}\)
= 1 + α1200
= 1 + 0.0043 × 1200 = 6.16
∴ I = \(\frac{1}{6.16}\) = 0.16 A.
2. In the circuit given below, the equivalent capacitance is ____________
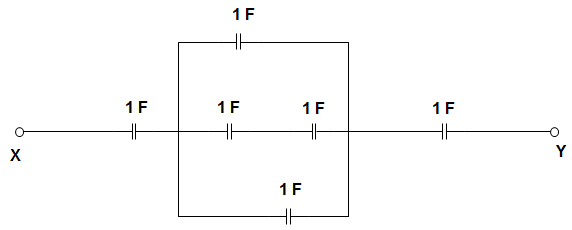
a) 1.625 F
b) 1.583 F
c) 0.583 F
d) 0.615 F
View Answer
Explanation: CCB = \(\left(\frac{C_2 C_3}{C_2+ C_3}\right)\) + C5 = 1.5 F
Now, CAB =\(\left(\frac{C_1 C_{CB}}{C_1+ C_{CB}}\right)\) + C6 = 1.6 F
CXY = \(\frac{C_{AB} × C_4}{C_{AB} + C_4}\) = 0.615 F.
3. In the circuit given below, the equivalent capacitance is ______________
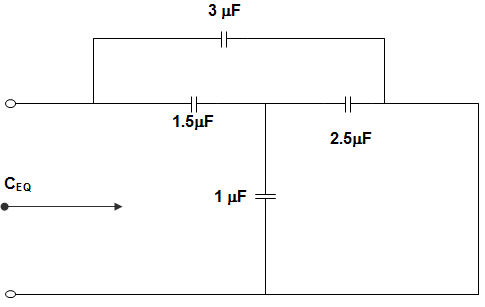
a) 3.5 μF
b) 1.2 μF
c) 2.4 μF
d) 4.05 μF
View Answer
Explanation: The 2.5 μF capacitor is in parallel with 1 μF capacitor and this combination is in series with 1.5 μF.
Hence, C1 = \(\frac{1.5(2.5+1)}{1.5+2.5+1}\)
= \(\frac{5.25}{5}\) = 1.05
Now, C1 is in parallel with the 3 μF capacitor.
∴ CEQ = 1.05 + 3 = 4.05 μF.
4. In the circuit given below, the voltage across A and B is?
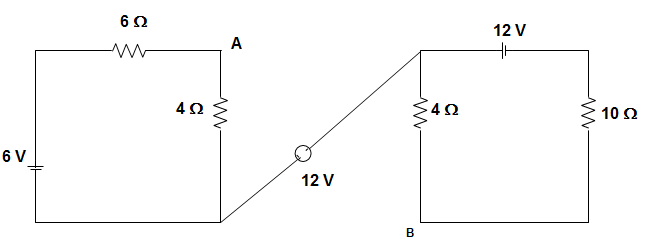
a) 13.04 V
b) 17.84 V
c) 12 V
d) 10.96 V
View Answer
Explanation: Loop current I1 = \(\frac{6}{10}\) = 0.6 A
I2 = \(\frac{12}{14}\) = 0.86 A
VAB = (0.6) (4) + 12 + (0.86) (4)
= 2.4 + 12 + 3.44
= 17.84 V.
5. In the figure given below, the voltage source provides the circuit with a voltage V. The number of non-planar graph of independent loop equations is ______________
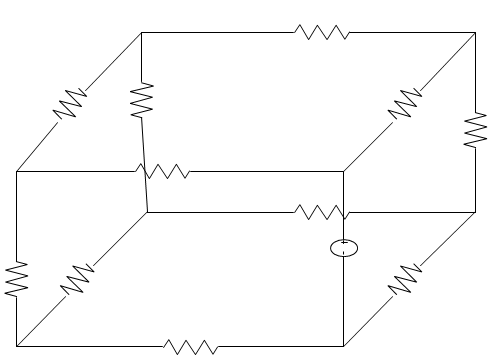
a) 8
b) 12
c) 7
d) 5
View Answer
Explanation: The total number of independent loop equations are given by L = B – N + 1 where,
L = number of loop equations
B = number of branches = 12
N = number of nodes = 8
∴ L = 12 – 8 + 1 = 5.
6. When a DC voltage is applied to an inductor, the current through it is found to build up in accordance with I = 20(1-e-50t). After the lapse of 0.02 s, the voltage is equal to 2 V. What is the value of inductance?
a) 2 mH
b) 5.43 mH
c) 1.54 mH
d) 0.74 mH
View Answer
Explanation: VL = L\(\frac{dI}{dt}\)
Where, I = 20(1-e-50t)
Therefore, VL = L\(\frac{d 20(1-e^{-50t})}{dt}\)
= L × 20 × 50e-50t
At t = 0.02 s, VL = 2 V
∴ L = \(\frac{2}{20 × 50 × e^{-50×0.02}}\)
= 5.43 μH.
7. An air capacitor of capacitance 0.005 μF is connected to a direct voltage of 500 V. It is disconnected and then immersed in oil with a relative permittivity of 2.5. The energy after immersion is?
a) 275 μJ
b) 250 μJ
c) 225 μJ
d) 625 μJ
View Answer
Explanation: E = \(\frac{1}{2}\) CV2
Or, C = \(\frac{ε_0 ε_r A}{d} = ϵ_r (\frac{ε_0 A}{d})\)
= 2.5 × 0.005 × 10-6
∴ CNEW = 12.5 × 10-9 F
Now, q = CV = 0.005 × 10-6 × 500 = 2.5 × 10-6
VNEW = \(\frac{q} {C_{NEW}}\)
= \(\frac{2.5 × 10^{-6}}{12.5 × 10^{-9}}\) VNEW = 200
E = \(\frac{1}{2}\) CV2
= \(\frac{1}{2}\) × 12.5 × 10-9 × (200)2
= 250 μJ.
8. The resistance of copper motor winding at t=20°C is 3.42 Ω. After extended operation at full load, the motor windings measures 4.22 Ω. If the temperature coefficient is 0.0426, what is the rise in temperature?
a) 60°C
b) 45.2°C
c) 72.9°C
d) 10.16°C
View Answer
Explanation: Given that, R1 = 3.42 Ω
T1 = 20° and α = 0.0426
R2 = 4.22 Ω
Now, \(\frac{R_1}{1 + αT_1} = \frac{R_2}{1 + αT_2}\)
Or, \(\frac{3.42}{1 + 0.0426 × 20} = \frac{4.22}{1 + 0.0426 T_2}\)
∴ Rise in temperature = T2 – T1
= 30.16 – 20
= 10.16°C.
9. A capacitor of capacitance 50 μF is connected in parallel to another capacitor of capacitance 100 μF. They are connected across a time-varying voltage source. At a particular time, the current supplied by the source is 5 A. The magnitude of instantaneous current through the capacitor of capacitance 50 μF is?
a) 1.57 A
b) 1.87 A
c) 1.67 A
d) 2.83 A
View Answer
Explanation: As the capacitors are in parallel, then the voltage V is given by,
V = \(\frac{1}{C_1} \int I_1 \,dt \)
∴ I1 = C1 \(\frac{dV}{dt}\)
That is, \(\frac{I_1}{I_2} = \frac{C_1}{C_2} = \frac{50}{100} = \frac{1}{2}\) ………………….. (1)
Also, I1 + I2 = 5 A ………………………….. (2)
Solving (1) and (2), we get, I1 = 1.67 A.
10. A capacitor of capacitance 50 μF is connected in parallel to another capacitor of capacitance 100 μF. They are connected across a time-varying voltage source. At a particular time, the current supplied by the source is 5 A. The magnitude of instantaneous current through the capacitor of capacitance 100 μF is?
a) 2.33 A
b) 3.33 A
c) 1.33 A
d) 4.33 A
View Answer
Explanation: As the capacitors are in parallel, then the voltage V is given by,
V = \(\frac{1}{C_2} \int I_2 \,dt \)
∴ I2 = C2 \(\frac{dV}{dt}\)
That is, \(\frac{I_1}{I_2} = \frac{C_1}{C_2} = \frac{50}{100} = \frac{1}{2}\) ………………….. (1)
Also, I1 + I2 = 5 A ………………………….. (2)
Solving (1) and (2), we get, I2 = 3.33 A.
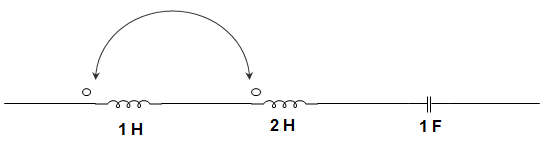
11. In the circuit given below, the resonant frequency is _______________
a) \(\frac{1}{2\sqrt{2} π}\) Hz
b) \(\frac{1}{2π}\) Hz
c) \(\frac{1}{4π}\) Hz
d) \(\frac{1}{\sqrt{2}2π}\) Hz
View Answer
Explanation: IEQ = L1 + L2 + 2M
LEQ = 1 + 2 + 2 × \(\frac{1}{2}\) = 4 H
∴ FO = \(\frac{1}{2π\sqrt{LC}} \)
= \(\frac{1}{2π\sqrt{4 × 1}} \)
= \(\frac{1}{4π}\) Hz.
12. In a series resonant circuit, VC = 300 V, VL = 300 V and VR = 100 V. What is the value of the source voltage?
a) Zero
b) 100 V
c) 350 V
d) 200 V
View Answer
Explanation: As VC and VL are equal, then XC is equal to XL and both the voltages are then cancelled out.
That is VS = VR
∴ VS = 100 V.
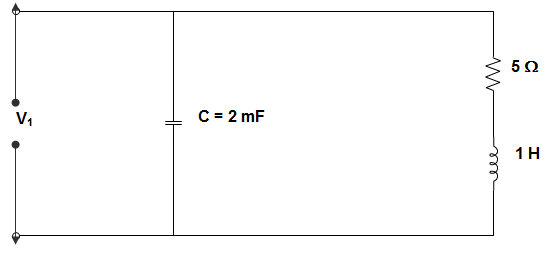
13. For the circuit given below, what is the value of the Q factor for the inductor?
a) 4.74
b) 4.472
c) 4.358
d) 4.853
View Answer
Explanation: QIN = \(\sqrt{\frac{L}{CR^2} – 1}\)
= \(\sqrt{\frac{1}{2 × 5^2 × 10^{-3} – 1}}\)
= \(\sqrt{\frac{1}{50 × 10^{-3} – 1}}\)
= \(\sqrt{19}\) = 4.358.
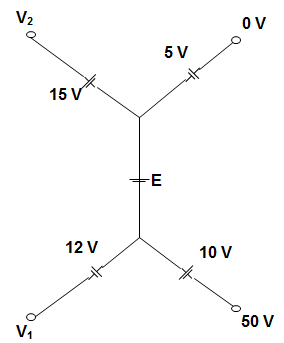
14. In the circuit given below, the value of the voltage source E is _______________
a) -65 V
b) 40 V
c) -60 V
d) 65 V
View Answer
Explanation: Going from 10 V to 0 V, we get,

50 + 10 + E + 5 = 0
Or, E + 65 = 0
Hence, E = -65 V.
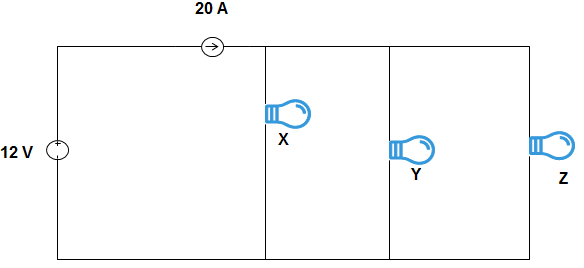
15. In the circuit given below, bulb X uses 48 W when lit, bulb Y uses 22 W when lit and bulb Z uses 14.4 W when lit. The number of additional bulbs in parallel to this circuit, that would be required to below the fuse is _______________
a) 4
b) 5
c) 6
d) 7
View Answer
Explanation: IX = \(\frac{48}{12}\) = 4 A
IY = \(\frac{22}{12}\) = 1.8 A
IZ = \(\frac{14.4}{12}\) = 1.2 A
Current required to below the fuse = 20 A
∴ Additional bulbs must draw current = 20 – (4 + 18 + 1.2)
= 20 – 7 = 13
∴ Number of additional bulbs required = \(\frac{13}{3}\) = 4.33
So, 4 additional bulbs are required.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
