This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Series-Series Connection of Two Port Network”.
1. In the circuit given below, the value of R is ___________
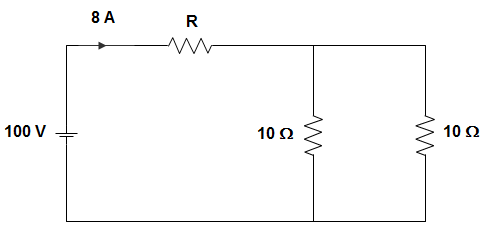
a) 2.5 Ω
b) 5.0 Ω
c) 7.5 Ω
d) 10.0 Ω
View Answer
Explanation: The resultant R when viewed from voltage source = \(\frac{100}{8}\) = 12.5
∴ R = 12.5 – 10 || 10 = 12.5 – 5 = 7.55 Ω.
2. In the circuit given below, the number of chords in the graph is ________________
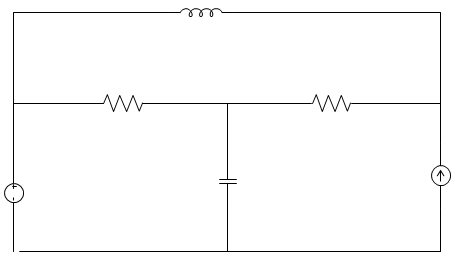
a) 3
b) 4
c) 5
d) 6
View Answer
Explanation: Given that, b = 6, n = 3
Number of Links is given by, b – n + 1
= 6 – 3 + 1 = 4.
3. In the circuit given below, the current through the 2 kΩ resistance is _____________
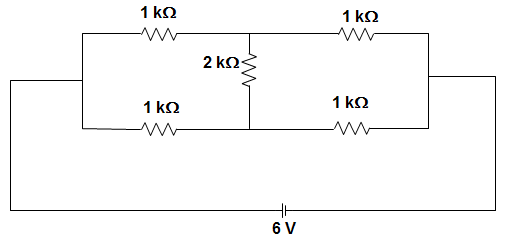
a) Zero
b) 1 mA
c) 2 mA
d) 6 mA
View Answer
Explanation: We know that when a Wheatstone bridge is balanced, no current will flow through the middle resistance.
Here, \(\frac{R_1}{R_2} = \frac{R_3}{R_4}\)
Since, R1 = R2 = R3 = R4 = 1 kΩ.
4. How many incandescent lamps connected in series would consume the same total power as a single 100 W/220 V incandescent lamp. The rating of each lamp is 200 W/220 V?
a) Not possible
b) 4
c) 3
d) 2
View Answer
Explanation: In series power = \(\frac{1}{P}\)
Now, \(\frac{1}{P} = \frac{1}{P_1} + \frac{1}{P_2}\)
= \(\frac{1}{200} + \frac{1}{200}\)
Or, P = \(\frac{200}{2}\) = 100 W.
5. Two networks are connected in series parallel connection. Then, the forward short-circuit current gain of the network is ____________
a) Product of Z-parameter matrices
b) Sum of h-parameter matrices
c) Sum of Z-parameter matrices
d) Product of h-parameter matrices
View Answer
Explanation: The forward short circuit current gain is given by,
h21 = \(\frac{I_2 (s)}{I_1 (s)}\), when V2 = 0
So, when the two networks are connected in series parallel combination,
[h11, h12; h21, h22] = [h’11 + h’11, h’12 + h’12; h’21 + h’21, h’22 + h’22]
So, h21 of total network will be sum of h parameter matrices.
6. The condition for a 2port network to be reciprocal is ______________
a) Z11 = Z22
b) BC – AD = -1
c) Y12 = -Y21
d) h12 = h21
View Answer
Explanation: If the network is reciprocal, then the ratio of the response transform to the excitation transform would not vary after interchanging the position of the excitation.
7. The relation AD – BC = 1, (where A, B, C and D are the elements of a transmission matrix of a network) is valid for ___________
a) Both active and passive networks
b) Passive but not reciprocal networks
c) Active and reciprocal networks
d) Passive and reciprocal networks
View Answer
Explanation: AD – BC = 1, is the condition for reciprocity for ABCD parameters, which shows that the relation is valid for reciprocal network. The ABCD parameters are obtained for the network which consists of resistance, capacitance and inductance, which indicates that it is a passive network.
8. For a 2 port network, the transmission parameters are given as 10, 9, 11 and 10 corresponds to A, B, C and D. The correct statement among the following is?
a) Network satisfies both reciprocity and symmetry
b) Network satisfies only reciprocity
c) Network satisfies only symmetry
d) Network satisfies neither reciprocity nor symmetry
View Answer
Explanation: Here, A = 10, B = 9, C = 11, D = 10
∴ A = D
∴ Condition for symmetry is satisfied.
Also, AD – BC = (10) (10) – (9) (11)
= 100 – 99 = 1
Therefore the condition of reciprocity is satisfied.
9. In the circuit given below, the equivalent capacitance is ______________
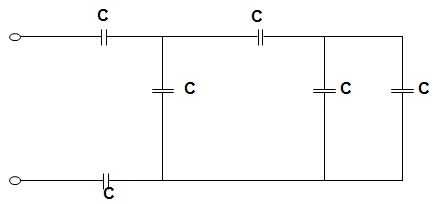
a) \(\frac{C}{4}\)
b) \(\frac{5C}{13}\)
c) \(\frac{5C}{2}\)
d) 3C
View Answer
Explanation: The equivalent capacitance by applying the concept of series-parallel combination of the capacitance is,
\(\frac{1}{C_{EQ}} = \frac{1}{C} + \frac{1}{C} + \frac{1}{5C/3}\)
= \(\frac{1}{C} + \frac{1}{C} + \frac{3}{5C} = \frac{1}{C}(\frac{5+5+3}{5})\)
Or, CEQ = \(\frac{5C}{13}\)
123 c Energy delivered during talk time
E = ∫ V(t)I(t) dt
Given, I (t) = 2 A = constant = 2 ∫ V(t)dt
= 2 × Shaded area
= 2 × \(\frac{1}{2}\) × (10 + 12) × 60 × 10
= 13.2 kJ.
10. In the circuit given below, the 60 V source absorbs power. Then the value of the current source is ____________
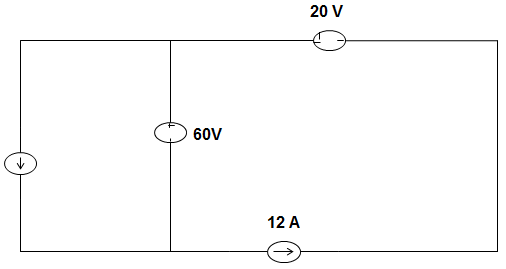
a) 10 A
b) 13 A
c) 15 A
d) 18 A
View Answer
Explanation: Given that, 60 V source is absorbing power, it means that current flow from positive to negative terminal in 60 V source.
Applying KVL, we get, I + I1 = 12 A ……………… (1)
Current source must have the value of less than 12 A to satisfy equation (1).
11. In the circuit given below, the number of node and branches are ______________
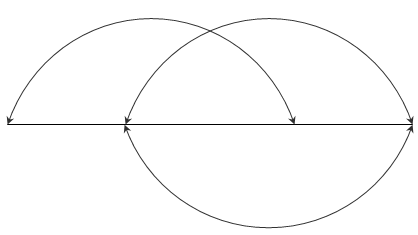
a) 4 and 5
b) 4 and 6
c) 5 and 6
d) 6 and 4
View Answer
Explanation: In the given graph, there are 4 nodes and 6 branches.
Twig = n – 1 = 4 – 1 = 3
Link = b – n + 1 = 6 – 4 + 1 = 3.
12. A moving coil of a meter has 250 turns and a length and depth of 40 mm and 30 mm respectively. It is positioned in a uniform radial flux density of 450 mT. The coil carries a current of 160 mA. The torque on the coil is?
a) 0.0216 N-m
b) 0.0456 N-m
c) 0.1448 N-m
d) 1 N-m
View Answer
Explanation: Given, N = 250, L = 40 × 10-3, d = 30 × 10-3m, I = 160 × 10-3A, B = 450 × 10-3 T
Torque = 250 × 450 × 10-3 × 40 × 10-3 × 30 × 10-3 × 160 × 10-3
= 200 × 10-6 N-m = 0.0216 N-m.
13. In the circuit given below, the equivalent inductance is ____________
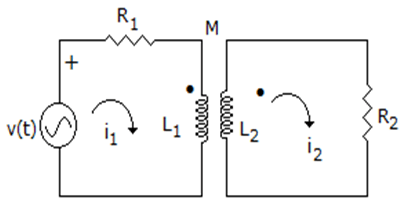
a) L1 + L2 – 2M
b) L1 + L2 + 2M
c) L1 + L2 – M
d) L1 + L2
View Answer
Explanation: Since, in one inductor current is leaving to dot and in other inductor current is entering to dot.
So, LEQ = L1 + L2 – 2M.
14. In the figure given below, the pole-zero plot corresponds to _____________
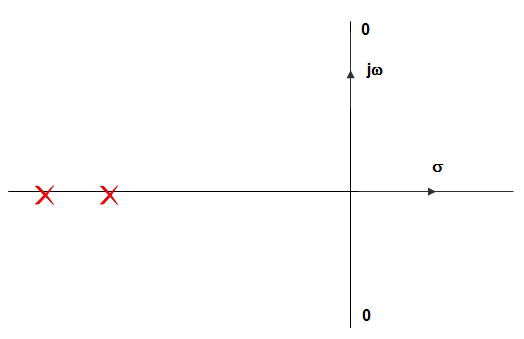
a) Low-pass filter
b) High-pass filter
c) Band-pass filter
d) Notch filter
View Answer
Explanation: In pole zero plot the two transmission zeroes are located on the jω-axis, at the complex conjugate location, and then the magnitude response exhibits a zero transmission at ω – ωC.
15. In the circuit given below, the maximum power that can be transferred to the resistor RL is _____________
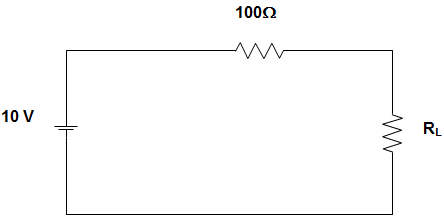
a) 1 W
b) 10 W
c) 0.25 W
d) 0.5 W
View Answer
Explanation: For maximum power transfer to the load resistor RL, RL must be equal to 100 Ω.
∴ Maximum power = \(\frac{V^2}{4R_L}\)
= \(\frac{10^2}{4 ×100}\) = 0.25 W.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Electronics & Communication Engineering MCQs
- Check Network Theory Books
- Check Electrical Engineering Books
- Apply for Electrical Engineering Internship
- Apply for Electronics & Communication Engineering Internship
