This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “DC Response of an R-L-C Circuit”.
1. For an R-L-C circuit, we get [D – (K1 + K2)][D – (K1 – K2)] i = 0. If K2 is positive, then the curve will be?
a) damped
b) over damped
c) under damped
d) critically damped
View Answer
Explanation: For an R-L-C circuit, we get [D – (K1 + K2)][D – (K1 – K2)] i = 0. If K2 is positive, then the curve will be over damped response.
2. If the roots of an equation are real and unequal, then the response will be?
a) critically damped
b) under damped
c) over damped
d) damped
View Answer
Explanation: If the roots of an equation are real and unequal, then the response will be over damped response. Over damped response of a system is defined as the system returns (exponentially decays) to equilibrium without oscillating.
3. If the roots of an equation are complex conjugate, then the response will be?
a) over damped
b) critically damped
c) damped
d) under damped
View Answer
Explanation: If the roots of an equation are complex conjugate, then the response will be under damped response. Damping is an influence within or upon an oscillatory system that has the effect of reducing, restricting or preventing its oscillations.
4. If the roots of an equation are real and equal, then the response will be?
a) over damped
b) damped
c) critically damped
d) under damped
View Answer
Explanation: If the roots of an equation are real and equal, then the response will be critically damped response. For a critically damped system, the system returns to equilibrium as quickly as possible without oscillating.
5. The circuit shown in the figure consists of resistance, capacitance and inductance in series with a 100V source when the switch is closed at t = 0. Find the equation obtained from the circuit in terms of current.
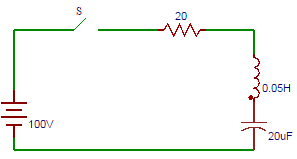
a) 100 = 20i + 0.05 \(\frac{di}{dt} + \frac{1}{20 \times 10^{-6}} \int idt\)
b) 100 = 20i – 0.05 \(\frac{di}{dt} + \frac{1}{20 \times 10^{-6}} \int idt\)
c) 100 = 20i + 0.05 \(\frac{di}{dt} – \frac{1}{20 \times 10^{-6}} \int idt\)
d) 100 = 20i – 0.05 \(\frac{di}{dt} – \frac{1}{20 \times 10^{-6}} \int idt\)
View Answer
Explanation: At t = 0, switch S is closed when the 100V source is applied to the circuit and results in the following differential equation.
100 = 20i + 0.05 \(\frac{di}{dt} + \frac{1}{20 \times 10^{-6}} \int idt\)
6. Replacing the differentiation with D1, D2 in the equation 100 = 20i + 0.05 \(\frac{di}{dt} + \frac{1}{20 \times 10^{-6}} \int idt\). Find the values of D1, D2.
a) 200±j979.8
b) -200±j979.8
c) 100±j979.8
d) -100±j979.8
View Answer
Explanation: Let the roots of the characteristic equation are denoted by D1, D2. So on differentiating the equation 100 = 20i + 0.05 \(\frac{di}{dt} + \frac{1}{20 \times 10^{-6}} \int idt\), we get D1 = -200+j979.8, D2 = -200-j979.8.
7. The expression of current from the circuit shown below.

a) i=e-200t [c1 cos979.8t+c2 979.8t]A
b) i=e200t [c1 cos979.8t-c2 979.8t]A
c) i=e-200t [c1 cos979.8t-c2 979.8t]A
d) i=e200t [c1 cos979.8t+c2 979.8t]A
View Answer
Explanation: The expression of current from the circuit will be i = eK1t[c1cosK1t + c2sinK2t]. So, i=e-200t [c1 cos979.8t+c2 979.8t]A.
8. At time t = 0, the value of current in the circuit shown below.

a) 1
b) 2
c) 3
d) 0
View Answer
Explanation: At t = 0 that is initially the current flowing through the circuit is zero that is i = 0. So, i = 0.
9. The voltage across the inductor at t = 0 in the circuit shown below.

a) 50
b) 100
c) 150
d) 200
View Answer
Explanation: At t = 0, that is initially the voltage across the inductor is 100V. => V = 100V. So we can write Ldi/dt = 100.
10. The current equation obtained from the circuit shown below is?

a) i=e-200t (1.04 sin979.8t)A
b) i=e-200t (2.04 sin979.8t)A
c) i=e-200t (3.04 sin979.8t)A
d) i=e-200t (4.04 sin979.8t)A
View Answer
Explanation: On solving the values of c1, c2 are obtained as c1 = 0, c2 = 2.04. So, the current equation is i=e-200t (2.04 sin979.8t)A.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Electrical Engineering MCQs
- Apply for Electrical Engineering Internship
- Apply for Electronics & Communication Engineering Internship
- Check Electrical Engineering Books
- Check Network Theory Books
