This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “Definition of the Laplace Transform”.
1. The Laplace transform of a function f (t) is?
a) \(\int_0^{\infty}\) f(t) e-st
b) \(\int_{-\infty}^0\) f(t) e-st
c) \(\int_0^{\infty}\) f(t) est
d) \(\int_{-\infty}^0\) f(t) est
View Answer
Explanation: The Laplace transform is a powerful analytical technique that is widely used to study the behavior of linear, lumped parameter circuits. L(f(t)) = F (s)
2. Laplace transform changes the ____ domain function to the _____ domain function.
a) time, time
b) time, frequency
c) frequency, time
d) frequency, frequency
View Answer
Explanation: Laplace transform changes the time domain function f (t) to the frequency domain function F(s). Similarly Laplace transformation converts frequency domain function F(s) to the time domain function f(t).
3. In the bilateral Laplace transform, the lower limit is?
a) 0
b) 1
c) ∞
d) – ∞
View Answer
Explanation: If the lower limit is 0, then the transform is referred to as one-sided or unilateral Laplace transform. In the two-sided or bilateral Laplace transform, the lower limit is – ∞.
4. The unit step is not defined at t =?
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: If k is 1, the function is defined as unit step function. And the unit step is not defined at t = 0.
5. The total period of the function shown in the figure is 4 sec and the amplitude is 10. Find the function f1 (t) from t = 0 to 1 in terms of unit step function.
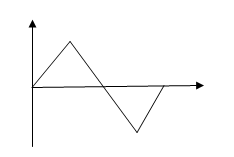
a) 10t [u (t) – u (t + 1)]
b) 10t [u (t) + u (t – 1)]
c) 10t [u (t) + u (t + 1)]
d) 10t [u (t) – u (t – 1)]
View Answer
Explanation: The function shown in the figure is made up of linear segments with break points at 0, 1, 3 and 4 seconds. From the graph, f1 (t) = 10t for 0 < t < 1. In terms of unit step function, f1 (t) = 10t [u (t) – u (t – 1)].
6. Find the function f2 (t) from the time t = 1 to 3 sec.
a) (-10t+20) [u (t-1) +u (t-3)]
b) (-10t+20) [u (t-1) – u (t-3)]
c) (-10t-20) [u (t-1) + u (t-3)]
d) (-10t-20) [u (t-1) – u (t-3)]
View Answer
Explanation: From the graph, f2 (t) = -10t + 20 for 1 < t < 3. In terms of unit step function, f2 (t) = (-10t+20) [u (t-1) – u (t-3)]. This function turn off at t = 1, turn off at t = 3.
7. Find the function f3 (t) from the time t = 3 to 4 sec.
a) (20t – 40) [u (t-3) – u (t-4)]
b) (20t + 40) [u (t-3) – u (t-4)]
c) (20t + 40) [u (t-3) + u (t-4)]
d) (20t – 40) [u (t-3) + u (t-4)]
View Answer
Explanation: From the graph, f3 (t) = 20t – 40 for 3 < t < 4. In terms of unit step function, f3 (t) = (20t – 40) [u (t-3) – u (t-4)]. This function turn off at t = 3, turn off at t = 4.
8. Find the expression of f (t) in the graph shown below.
a) 10t [u (t) – u (t – 1)] – (-10t+20) [u (t-1) – u (t-3)] + (20t – 40) [u (t-3) – u (t-4)]
b) 10t [u (t) – u (t – 1)] – (-10t+20) [u (t-1) – u (t-3)] – (20t – 40) [u (t-3) – u (t-4)]
c) 10t [u (t) – u (t – 1)] + (-10t+20) [u (t-1) – u (t-3)] + (20t – 40) [u (t-3) – u (t-4)]
d) 10t [u (t) – u (t – 1)] + (-10t+20) [u (t-1) – u (t-3)] – (20t – 40) [u (t-3) – u (t-4)]
View Answer
Explanation: We use the step function to initiate and terminate these linear segments at the proper times. The expression of f (t) is f (t) = 10t [u (t) – u (t – 1)] + (-10t+20) [u (t-1) – u (t-3)] + (20t – 40) [u (t-3) – u (t-4)].
9. In the graph shown below, find the expression f (t).
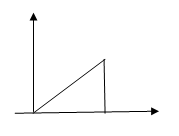
a) 2t
b) 3t
c) 4t
d) 5t
View Answer
Explanation: The waveform shown in the figure starts at t = 0 and ends at t = 5 sec. The equation for the above waveform is f (t) = 4t.
10. Find the function f (t) in terms of unit step function in the graph shown below.
a) 4t [u (t) – u (t + 5)]
b) 4t [u (t) + u (t + 5)]
c) 4t [u (t) – u (t – 5)]
d) 4t [u (t) + u (t – 5)]
View Answer
Explanation: The waveform shown in the figure starts at t = 0 and ends at t = 5 sec. In terms of unit step function the waveform can be expressed as f (t) = 4t [u (t) – u (t – 5)].
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Electronics & Communication Engineering MCQs
- Practice Electrical Engineering MCQs
- Apply for Electrical Engineering Internship
- Apply for Electronics & Communication Engineering Internship
- Check Network Theory Books
