The Potential Energy of a Spring - Class 11 Physics MCQ

This set of Class 11 Physics Chapter 6 Multiple Choice Questions & Answers (MCQs) focuses on “The Potential Energy of a Spring”.

1. The potential energy possessed by a spring is also known as _____
a) Elastic potential energy
b) Extensive potential energy
c) Compressive potential energy
d) Deflection potential energy
View Answer

Answer: a
Explanation: The potential energy stored in a spring is the consequence of its elastic property and hence it is also termed “elastic potential energy”. It can be stored when the spring is extended or compressed.

2. An object is travelling at a velocity of 10 m/s. It has a mass of 2 kg. It impacts a spring of spring constant “k” as shown in the figure. What is the compression of the spring?

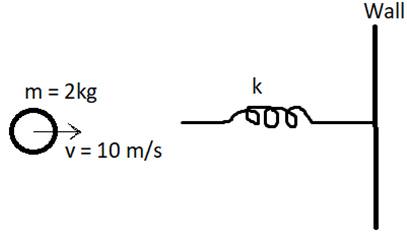
a) 10 x (2/k) ^0.5
b) 10 x (200/k) ^0.5
c) (200/k)
d) (200/k) ²
View Answer

Answer: a
Explanation: From the law of conservation of energy;
1/2 x m x v² = 1/2 x k x d²
2 x 10² = k x d²
200/k = d²
d = (200/k) ^0.5
= 10 x (2/k) ^0.5.

3. How much should a spring of indefinite length be compressed to have a potential energy equivalent to a ball of mass 6 kg raised to a height of 120 m above the ground? Let the spring have a stiffness of k = 100 N/m and assume g = 10 m/s².
a) 6m
b) 12m
c) 20m
d) 144m
View Answer

Answer: b
Explanation: PE of ball = m x g x h
= 6 x 10 x 120
= 7200 J
PE of spring = 1/2 x k x d²
Given;
PE of ball = PE of spring
7200 = 1/2x k x d²
= 1/2 x 100 x d²
d² = 144
d = 12 m.

4. The following graph represents theparabolic plots of the potential energy V andkinetic energy K ofa block attached to aspring obeying Hooke’s law.

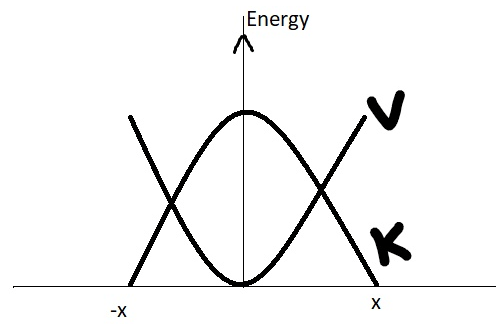
a) True
b) False
View Answer

Answer: a
Explanation: The following graph represents the parabolic plots of the potential energy V and kinetic energy K of a block attached to a spring obeying Hooke’s law.The two plotsare complementary, onedecreasing as theother increases. The total mechanicalenergy E = K + V remains constant.

5. Find the energy equation for the system shown in the figure. “m” is the mass of the block moving at a velocity “v”, “k” is the spring constant, “q” is the coefficient of friction of the floor and let “d” be the compression in the spring.

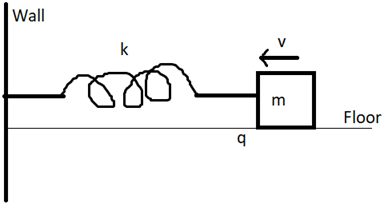
a) 1/2*m*v²⁺ = 1/2*k*d² + q*m*g*d
b) 1/2*m*v²⁺ + 1/2*k*d² + q*m*g*d = 0
c) -1/2*m*v²⁺ = 1/2*k*d² + q*m*g*d
d) 1/2*m*v²⁺ – 1/2*k*d² + q*m*g*d = 0
View Answer

Answer: a
Explanation: Work done by velocity (W1) = 1/2 x m x v²
Work done by spring (W2) = 1/2 x k x d²
Work done by friction (W3) = q x m x g x d
Since the work done by spring and friction are opposite to that of the work done by the velocity, we have;
W1 – W2 – W3 = 0
W1 = W2 + W3
Therefore;
1/2*m*v²⁺ = 1/2*k*d² + q*m*g*d.

Note: Join free Sanfoundry classes at Telegram or Youtube

6. Assume a spring extend by “d” due to some load. Let “F” be the spring force and “k’ the spring constant. Then, the potential energy stored is _____
a) 2d/F²
b) F²/2k
c) 2k/T²
d) F²/2d
View Answer

Answer: b
Explanation: F = k*d
PE = 1/2*k*d²
= 1/2*F*d
= 1/2*F*F/k
= F²/2k.

7. A spring of length 1m has two cars connected to both of its ends. The two cars move towards eachother such that the spring is compressed to 0.5m. If the spring constant is 500 N/m, what is the elastic potential energy stored?
a) 125 J
b) -125 J
c) 62.5 J
d) -62.5 J
View Answer

Answer:c
Explanation: PE = 1/2*k*d²
= 1/2 x 500 x (-0.5) ²
= 62.5 J.
The elastic potential energy is positive even for negative displacement.

8. What is the increase in potential energy storage when the compression distance is doubled in a spring obeying Hooke’s law?
a) No increase
b) 100% increase
c) Cannot be determined
d) 4 times
View Answer

Answer: d
Explanation: PE = 1/2 x k x d²
The elastic potential energy stored is directly proportional to the square of the compression. Hence, a two-fold increase in compression will result in potential energy storage to increase by four times.

9. The elastic potential energy varies linearly with displacement.
a) True
b) False
View Answer

Answer: b
Explanation: PE = 1/2 x k x d²; where d = Displacement
Equation of parabola: y = 4x²
By comparing the two equations, we can conclude that the elastic potential energy varies parabolically with displacement and not linearly.

Sanfoundry Global Education & Learning Series – Physics – Class 11.

To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 11 Physics MCQ – Potential Energy

» Next - Class 11 Physics MCQ – Various Forms of Energy : The Law of Conservation of Energy

Related Posts:

Recommended Articles: