This set of Class 11 Physics Chapter 8 Multiple Choice Questions & Answers (MCQs) focuses on “Gravitation – Earth Satellite – 1”.
1. The satellites orbiting the earth, eventually fall to the earth when they are left unsupervised or unattended because _____
a) their power supply runs out
b) of viscous forces causing the speed of the satellite and hence height to gradually decrease
c) the laws of gravitation predict such a trajectory
d) of collisions with other satellites
View Answer
Explanation: Due to the presence of some gases of the atmosphere and other debris, the satellites speed is reduced due to viscous forces. This reduces the height of the satellite. Hence, it eventually falls to the earth.
2. The time period of the moon around the earth is 24 hours.
a) True
b) False
View Answer
Explanation: The time period of the moon around the earth cannot be 24 hours because then it would be a geostationary satellite. However, we know it is not true. The time period of the moon around the earth is found to be approximately 27.3 earth days.
3. Consider 2 satellites A and B having time periods 16 hours and 1 hour, respectively. What is the ratio of the radius of their orbits?
a) 4:1
b) 8:1
c) 16:1
d) 64:1
View Answer
Explanation: The time periods (T) of a satellite revolving around the earth of radius R and at height h is:
T = 2 x pi x [(R + h)3 / (G X M)]1/2
Hence, the time period is directly proportional to (R + h)3/2
The ratio of orbits is, therefore, 64:1.
4. A satellite is launched into a circular orbit of radius R while a second satellite is launched into an orbit of radius 1.02R. What is the percentage change in the time periods of the two satellites?
a) 0.7
b) 1
c) 1.5
d) 3
View Answer
Explanation: The time periods (T) of a satellite revolving around the earth of radius R and at height h is:
T = 2 x pi x [(R + h)3 / (G X M)]1/2
Hence, the time period is directly proportional to (R + h)3/2
From this, we have the ratio of the time periods as 1.03.
1.03 x 100 = 103. Hence, there is a 3% change in the time period.
5. A satellite is revolving very close to a planet of density D. What is the time period of that satellite?
a) [3/(D*G)]1/2
b) [3/(D*G)]3/2
c) [3/(2*D*G)]1/2
d) [(3*G)/D]1/2
View Answer
Explanation: The time period of a satellite flying very close to the surface of the earth is;
T = 2 x pi x [R3 / (G X M)]1/2; [Height is negligible compared to the radius of the earth].
Mass (M) = Density (D) x Volume
M = D x (4/3 x pi x R3)
Substituting the relation of mass into the time period, we get;
T = [3/(2 x D x G)]1/2
6. The orbital velocity of a satellite orbiting a planet of mass “M” and radius “R” at a height as shown is [(G*M)/(R+h)].
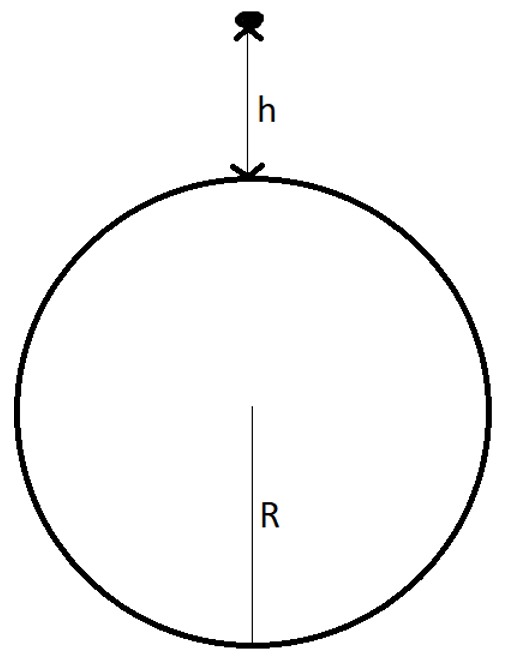
a) True
b) False
View Answer
Explanation: Let the mass of the satellite be “m”.
The gravitational force (F) = (G x m x M)/(R + h)2
The centripetal force (F’) = (m x v2)/(R + h); v = Orbital velocity
Due to equilibrium, F = F’;
(G x m x M)/(R + h)2 = (m x v2)/(R + h)
Therefore; v = [(G*M)/(R+h)]1/2
7. A satellite orbits the earth at a height of R/5. What is its orbital speed?
a) [(2*G*M)/(R)]1/2
b) [(G*M)/(R)]1/2
c) [(G*M)/(7*R)]1/2
d) [(5*G*M)/(6*R)]1/2
View Answer
Explanation: The orbital velocity of a satellite flying at a height “h” above the surface of the earth of radius “R” is:
v = [(G*M)/(R+h)]1/2
Here, h = R/5
Therefore; v = [(5*G*M)/(6*R)]1/2
8. The time period of a satellite is independent of the mass of the satellite.
a) True
b) False
View Answer
Explanation: For a satellite of mass “m” revolving around a planet of mass “M” and radius
“R” at a height “h” above the surface, the satellite traverses a distance [2 x pi x (R + h)] in time “T” if the orbital velocity is “v”.
Hence, the time periods (T) = [2 x pi x (R + h)]/v
We know; orbital velocity (v) = [(G x M)/(R+h)]1/2
Hence; T = [2 x pi x (R + h)3/2/(G X M)½], which is independent of the mass of the satellite.
9. A satellite of mass “m” revolves around a planet at a height as shown in the figure. If “g” is the acceleration due to gravity on the surface of the planet, what is the orbital velocity of the satellite?

a) gh/2
b) (gR)/(R-h)
c) (gR2)/(R+h)
d) [(gR2)/(R+h)]1/2
View Answer
Explanation: Orbital velocity (v) = [(G*M)/(R+h)]1/2
g = (G*M)/R2
(G*M) = g*R2
Therefore; v = [(gR2)/(R+h)]1/2
10. The time period of a satellite of earth is 90 minutes. If the separation between the earth and the satellite is quadrupled, the new time period will be _____________
a) 90 minutes
b) 180 minutes
c) 560 minutes
d) 720 minutes
View Answer
Explanation: The time period is directly proportional to the radius of orbit raised to the power of 1.5.
If the radius is quadrupled, the time period increases by 8 times.
Hence, the new time period = 90 x 8 = 720 minutes.
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Biology MCQs
- Practice Class 11 - Mathematics MCQs
- Check Class 11 - Physics Books
- Practice Class 11 - Chemistry MCQs
