This set of Physics Problems for IIT JEE Exam focuses on “Energy Stored in a Capacitor”.
1. Pick out the expression for energy stored in a capacitor from the following.
a) U = 2CV2
b) U = \(\frac {1}{2}\) (Q2C)
c) U = \(\frac {1}{2}\) (QV)
d) U = \(\frac {1}{2} (\frac {C}{V^2})\)
View Answer
Explanation: Work done in charging a capacitor gets stored in the capacitor in the form of its electric potential energy and this is known as energy stored in a capacitor. The expression is given by:
U = \(\frac {1}{2}\) (CV2) = \(\frac {1}{2}\) (QV) = \(\frac {1}{2} (\frac {Q^2}{C})\)
The unit is for this quantity is joule.
2. Find the energy stored in the capacitor between the terminals A and B of the combination shown below. Given – Capacitance of each capacitor C = 1μF
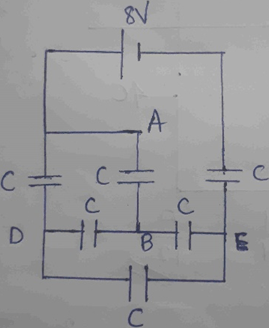
a) 12 μF
b) 8 μF
c) 4 μF
d) 10 μF
View Answer
Explanation: We can simplify the given diagram as given below:
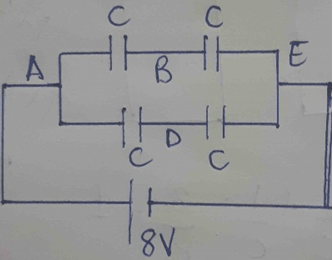
In the first row, both the capacitors are in series, so, the equivalent capacitance = \(\frac {1}{C} + \frac {1}{C} = \frac {2}{C} \rightarrow \frac {C}{2}\)
Similarly, in the second row also, they are in series, so equivalent capacitance = \(\frac {C}{2}\)
Total capacitance = \(\frac {C}{2} + \frac {C}{2}\) = C
Charge (Q) = CV
Charge on the capacitor between the terminals A and B of the network → \(\frac {Q}{2} = \frac {CV}{2}\)
Thus, energy stored in the capacitor (U) = \(\frac {(\frac {Q}{2})^2}{2C} = \frac {Q^2}{4}\) × 2C = \(\frac {C^2V^2}{8C} = \frac {CV^2}{8}\)
C = 1μF; V = 8V (Given)
Substituting the values of C and V
U = (1 × 10-6) × 8 × \(\frac {8}{8}\) = 8 × 10-6 = 8μJ
Therefore, the energy stored is 8μJ.
3. A capacitor of capacitance 5μF is charged to 50 V and another capacitor of capacitance 7μF is charged to 42 V. These two are connected together. On doing so, what is the energy lost by the 5μF capacitor?
a) 2.35 mJ
b) 2.45 mJ
c) 2.55 mJ
d) 2.25 mJ
View Answer
Explanation: Common potential, V = \( \frac {(C_1V_1 + C_1V_2)}{(C_1 + C_2)}\)
V = \( \frac {[(5 \times 50) + (7 \times 40)] \times 10^{-6}}{(5 + 7) \times 10^{-6}}\)
V = \( \frac {(250 + 280)}{12}\) = 44.4 V
Energy lost by 5 μF capacitor = \(\frac {1}{2}\)C1V12 – \(\frac {1}{2}\)C1V2 = \(\frac {1}{2}\)C (V12 – V2)
\(\frac {1}{2}\) × (5 × 10-6) × (502 – 402) = 0.00225
U = 2.25 × 10-3 J
U = 2.25 mJ
Therefore, the energy lost is 2.25 mJ
4. In a capacitor, energy is stored in the form of electric field.
a) True
b) False
View Answer
Explanation: Yes, the energy in a capacitor is stored in electric fields, between its plates. A capacitor is a device that is used to store energy or charges. It is also used for extracting energy from an electric field. When a capacitor is being charged, an electric field is builds up.
5. Initially the potential difference of a 8 μF capacitor is 30 V. Then it is changed to 40 V. What is the increase in energy?
a) 28 × 10-4 J
b) 18 × 10-4 J
c) 8 × 10-4 J
d) 24 × 10-4 J
View Answer
Explanation: The required equation for the increase in energy is given by:
U2 – U1 = \(\frac {1}{2}\) × C (V22 – V12)
= \(\frac {1}{2}\) × 8 × 10-6 × (402 – 302)
= \(\frac {1}{2}\) × 8 × 10-6 × 700
= 4 × 700 × 10-6
= 2800 × 10-6
= 28 × 10-4 J
Therefore, the increase in energy is 28 × 10-4 J.
6. A 6 μF capacitor is charged by a 100V supply. It is then disconnected from the supply and μ is connected to another uncharged 3μF capacitor. How much electrostatic energy of the first capacitor is dissipated in the form of heat and electromagnetic radiation?
a) 3 x 10-2 J
b) 2 x 10-2 J
c) 1 x 10-2 J
d) 4 x 10-2 J
View Answer
Explanation: Given: C1 = 6μF; V1 = 100 V
Initial energy stored (U1) = \(\frac {1}{2}\) C1V12 = \(\frac {1}{2}\) × 6 × 10-6 × 100 × 100
= 3 × 10-2 J
Potential (V) = \(\frac {C_1V_1}{(C_1+C_2)}\)
= 6 × 10-6 × \(\frac {100}{(6+3)}\) × 10-6
= \(\frac {600}{9}\) V
Final energy (U2) = \(\frac {1}{2}\) (C1 + C2) × V2
= \(\frac {1}{2}\) × 9 × 10-6 × \(\frac {1}{2} \times \frac {600}{9} \times \frac {600}{9}\)
= 2 × 10-2 J
Therefore, the energy dissipated in the form of heat and electromagnetic radiation is:
U2 – U1 = 3 × 10-2 – 2 × 10-2
U2 – U1 = 1 × 10-2 J
7. What is the maximum energy that can be stored in a capacitor?
a) Depends on the maximum area of the capacitor
b) Depends on the maximum resistance offered
c) Depends on the maximum electric field
d) Depends on the maximum current passing through the capacitor
View Answer
Explanation: The maximum energy that can be desirably stored in a capacitor is depends on the maximum electric field that the dielectric can withstand without breaking down. Therefore, capacitors of the same type have about the same maximum energy density, i.e. joules of energy per cubic meter.
Sanfoundry Global Education & Learning Series – Physics – Class 12.
To practice Physics Problems for IIT JEE Exam, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Get Free Certificate of Merit in Physics - Class 12
- Participate in Physics - Class 12 Certification Contest
- Become a Top Ranker in Physics - Class 12
- Take Physics - Class 12 Tests
- Chapterwise Practice Tests: Chapter 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Chapterwise Mock Tests: Chapter 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Practice Class 12 - Chemistry MCQs
- Practice Class 12 - Biology MCQs
- Buy Class 12 - Physics Books
- Practice Class 11 - Physics MCQs
- Practice Class 12 - Mathematics MCQs
